Багатофакторні сплайни адаптивної регресії в r

Сплайни багатовимірної адаптивної регресії (MARS) можна використовувати для моделювання нелінійних зв’язків між набором змінних предиктора та змінною відповіді .

Цей метод працює наступним чином:

1. Розділіть набір даних на k частин.

2. Пристосуйте регресійну модель до кожної частини.

3. Використовуйте k-кратну перехресну перевірку, щоб вибрати значення для k .

Цей підручник надає покроковий приклад того, як адаптувати модель MARS до набору даних у R.

Крок 1: Завантажте необхідні пакети

Для цього прикладу ми використаємо набір даних ISLR Wage .   пакет, який містить річну зарплату 3000 людей разом із різними прогнозними змінними, такими як вік, освіта, раса тощо.

Перед підгонкою моделі MARS до даних ми завантажимо необхідні пакети:

 library (ISLR) #contains Wage dataset
library (dplyr) #data wrangling
library (ggplot2) #plotting
library (earth) #fitting MARS models
library (caret) #tuning model parameters

Крок 2: Перегляньте дані

Далі ми відобразимо перші шість рядків набору даних, з яким ми працюємо:

 #view first six rows of data
head (Wage)

       year age maritl race education region
231655 2006 18 1. Never Married 1. White 1. < HS Grad 2. Middle Atlantic
86582 2004 24 1. Never Married 1. White 4. College Grad 2. Middle Atlantic
161300 2003 45 2. Married 1. White 3. Some College 2. Middle Atlantic
155159 2003 43 2. Married 3. Asian 4. College Grad 2. Middle Atlantic
11443 2005 50 4. Divorced 1. White 2. HS Grad 2. Middle Atlantic
376662 2008 54 2. Married 1. White 4. College Grad 2. Middle Atlantic
             jobclass health health_ins logwage wage
231655 1. Industrial 1. <=Good 2. No 4.318063 75.04315
86582 2. Information 2. >=Very Good 2. No 4.255273 70.47602
161300 1. Industrial 1. <=Good 1. Yes 4.875061 130.98218
155159 2. Information 2. >=Very Good 1. Yes 5.041393 154.68529
11443 2. Information 1. <=Good 1. Yes 4.318063 75.04315
376662 2. Information 2. >=Very Good 1. Yes 4.845098 127.11574

Крок 3: Створення та оптимізація моделі MARS

Далі ми створимо модель MARS для цього набору даних і виконаємо k-кратну перехресну перевірку , щоб визначити, яка модель дає найнижчу тестову RMSE (середню квадратичну помилку).

 #create a tuning grid
hyper_grid <- expand. grid (degree = 1:3,
                          nprune = seq (2, 50, length.out = 10) %>%
floor ())

#make this example reproducible
set.seed(1)

#fit MARS model using k-fold cross-validation
cv_mars <- train(
  x = subset(Wage, select = -c(wage, logwage)),
  y = Wage$wage,
  method = " earth ",
  metric = " RMSE ",
  trControl = trainControl(method = " cv ", number = 10),
  tuneGrid = hyper_grid)

#display model with lowest test RMSE
cv_mars$results %>%
  filter (nprune==cv_mars$bestTune$nprune, degree =cv_mars$bestTune$degree)    
degree nprune RMSE Rsquared MAE RMSESD RsquaredSD MAESD		
1 12 33.8164 0.3431804 22.97108 2.240394 0.03064269 1.4554

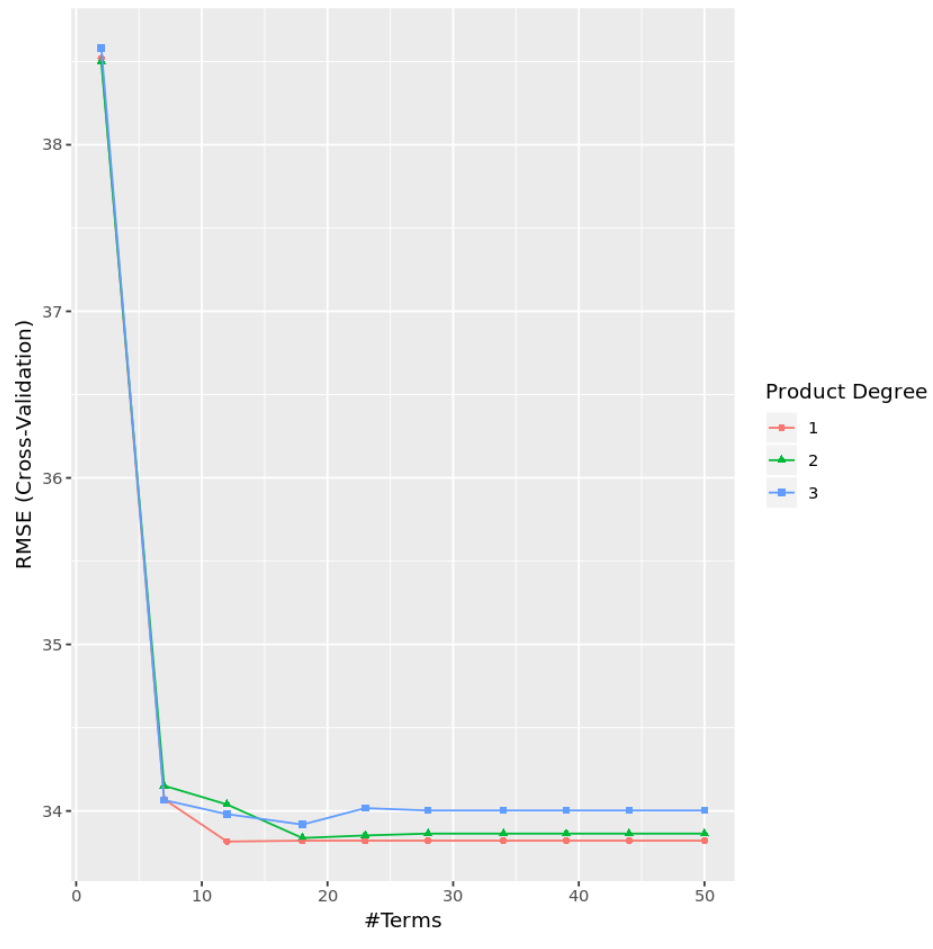
З результатів ми бачимо, що модель, яка дала найнижчу тестову MSE, була моделлю лише з ефектами першого порядку (тобто без умов взаємодії) і 12 умовами. Ця модель дала середньоквадратичну помилку (RMSE) 33,8164 .

Примітка: ми використали method=”earth” для визначення моделі MARS. Ви можете знайти документацію для цього методу тут .

Ми також можемо створити діаграму для візуалізації тесту RMSE на основі ступеня та кількості термінів:

 #display test RMSE by terms and degree
ggplot(cv_mars)

На практиці ми б адаптували модель MARS до кількох інших типів моделей, таких як:

• Множинна лінійна регресія
• Поліноміальна регресія
• Пікова регресія
• Регресія ласо
• Регресія головних компонент
• Часткові найменші квадрати

Потім ми порівнюємо кожну модель, щоб визначити, яка призводить до найменшої помилки тесту, і вибираємо цю модель як оптимальну для використання.

Повний код R, використаний у цьому прикладі, можна знайти тут .