Що таке стандартизована тестова статистика?
Статистична гіпотеза — це припущення щодо параметра сукупності . Наприклад, можна припустити, що середній зріст чоловіка в Сполучених Штатах становить 70 дюймів. Гіпотеза щодо зростання є статистичною гіпотезою , а справжній середній зріст чоловіка в Сполучених Штатах є параметром чисельності населення .
Перевірка гіпотези — це формальний статистичний тест, який ми використовуємо, щоб відхилити або не відхилити статистичну гіпотезу.
Основний процес виконання перевірки гіпотези такий:
1. Зберіть вибіркові дані.
2. Обчисліть статистику стандартизованого тесту для даних вибірки.
3. Порівняйте статистику стандартизованого тесту з критичним значенням. Якщо воно є більшим за критичне значення, відхиліть нульову гіпотезу. В іншому випадку не відкидайте перевірку нульової гіпотези.
Формула, яку ми використовуємо для розрахунку стандартизованої тестової статистики, залежить від типу перевірки гіпотези, яку ми виконуємо.
У наведеній нижче таблиці показано формулу для розрахунку стандартизованої тестової статистики для кожного з чотирьох основних типів перевірки гіпотез:
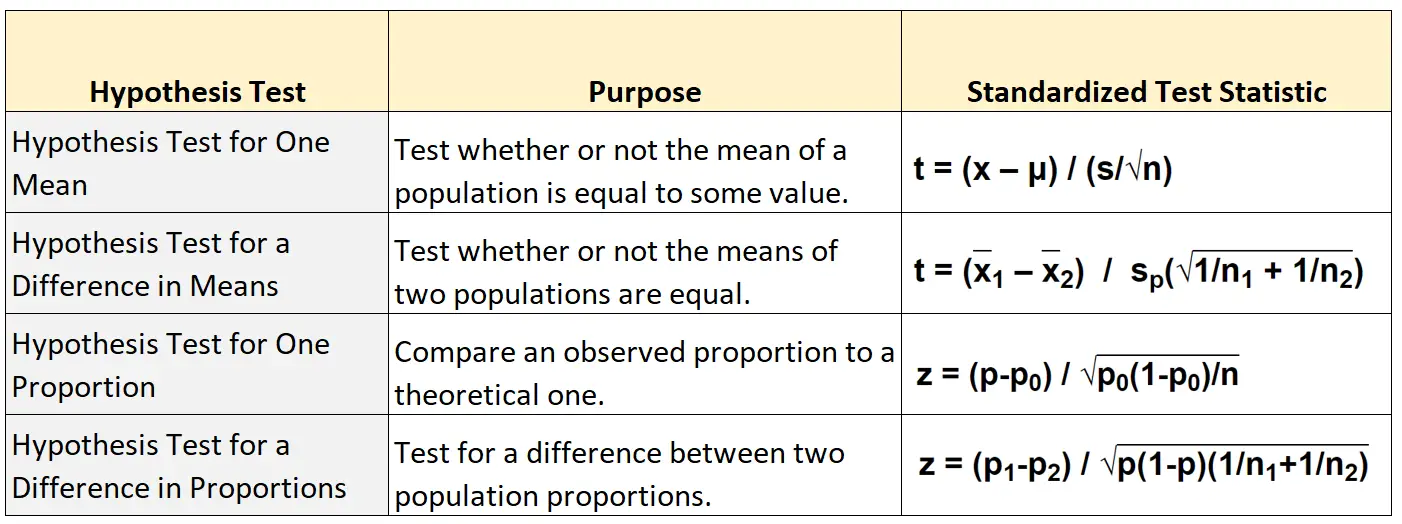
Перевірка гіпотези для середнього
Одновибірковий t-критерій використовується, щоб перевірити, чи дорівнює середнє значення сукупності певному значенню.
Стандартизована тестова статистика для цього типу тесту розраховується таким чином:
t = ( X – μ) / (s/√n)
золото:
- x: вибіркове середнє
- μ 0 : гіпотетична середня популяція
- s: вибіркове стандартне відхилення
- n: розмір вибірки
Зверніться до цього підручника , щоб отримати приклад обчислення цієї стандартизованої тестової статистики.
Перевірка гіпотези на різницю в середніх
Двовибірковий t-критерій використовується, щоб перевірити, чи рівні середні дві сукупності чи ні.
Стандартизована тестова статистика для цього типу тесту розраховується таким чином:
t = ( X 1 – X 2 ) / s p (√ 1/n 1 + 1/n 2 )
де x 1 і x 2 — середні значення вибірки, n 1 і n 2 — розміри вибірки, а s p обчислюється наступним чином:
s p = √ (n 1 -1)s 1 2 + (n 2 -1)s 2 2 / (n 1 +n 2 -2)
де s 1 2 і s 2 2 – вибіркові дисперсії.
Зверніться до цього підручника , щоб отримати приклад обчислення цієї стандартизованої тестової статистики.
Перевірка гіпотези пропорції
Однопропорційний z-тест використовується для порівняння спостережуваної пропорції з теоретичною пропорцією.
Стандартизована тестова статистика для цього типу тесту розраховується таким чином:
z = (pp 0 ) / √ p 0 (1-p 0 )/n
золото:
- p: досліджувана пропорція зразка
- p 0 : гіпотетична частка населення
- n: розмір вибірки
Зверніться до цього підручника , щоб отримати приклад обчислення цієї стандартизованої тестової статистики.
Перевірка гіпотези на різницю в пропорціях
Двопропорційний z-тест використовується для перевірки різниці між двома пропорціями населення.
Стандартизована тестова статистика для цього типу тесту розраховується таким чином:
z = (p 1 -p 2 ) / √ p(1-p)(1/n 1 +1/n 2 )
де p 1 і p 2 — пропорції вибірки, n 1 і n 2 — розміри вибірки, і де p — загальна об’єднана частка, розрахована таким чином:
p = (p 1 n 1 + p 2 n 2 )/(n 1 + n 2 )
Зверніться до цього підручника , щоб отримати приклад обчислення цієї стандартизованої тестової статистики.
Про автора
Редакція
Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше