Як обчислити стандартну помилку регресії в excel

Ми підбираємо лінійну регресійну модель , модель має такий вигляд:

Y = β ₀ + β ₁ X + … + β _i

де ϵ — помилка, яка не залежить від X.

Незалежно від того, як X можна використовувати для прогнозування значень Y, у моделі завжди буде випадкова помилка.

Одним із способів вимірювання дисперсії цієї випадкової помилки є використання стандартної помилки регресійної моделі , яка є способом вимірювання стандартного відхилення залишків ϵ.

Цей підручник містить покроковий приклад того, як обчислити стандартну помилку регресійної моделі в Excel.

Крок 1: Створіть дані

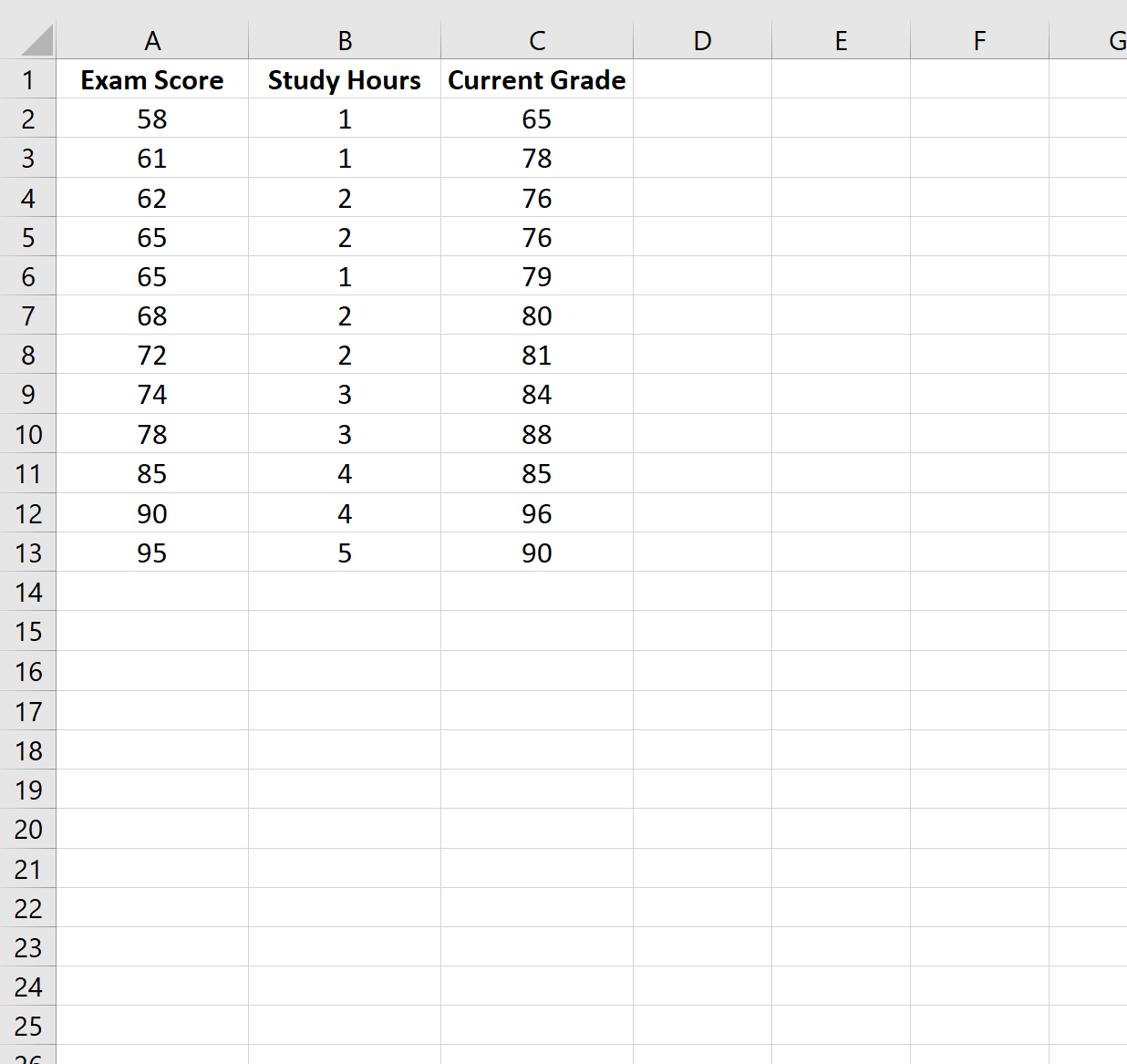
Для цього прикладу ми створимо набір даних, що містить такі змінні для 12 різних студентів:

• Результат іспиту
• Години, витрачені на навчання
• Поточний клас

Крок 2. Підберіть регресійну модель

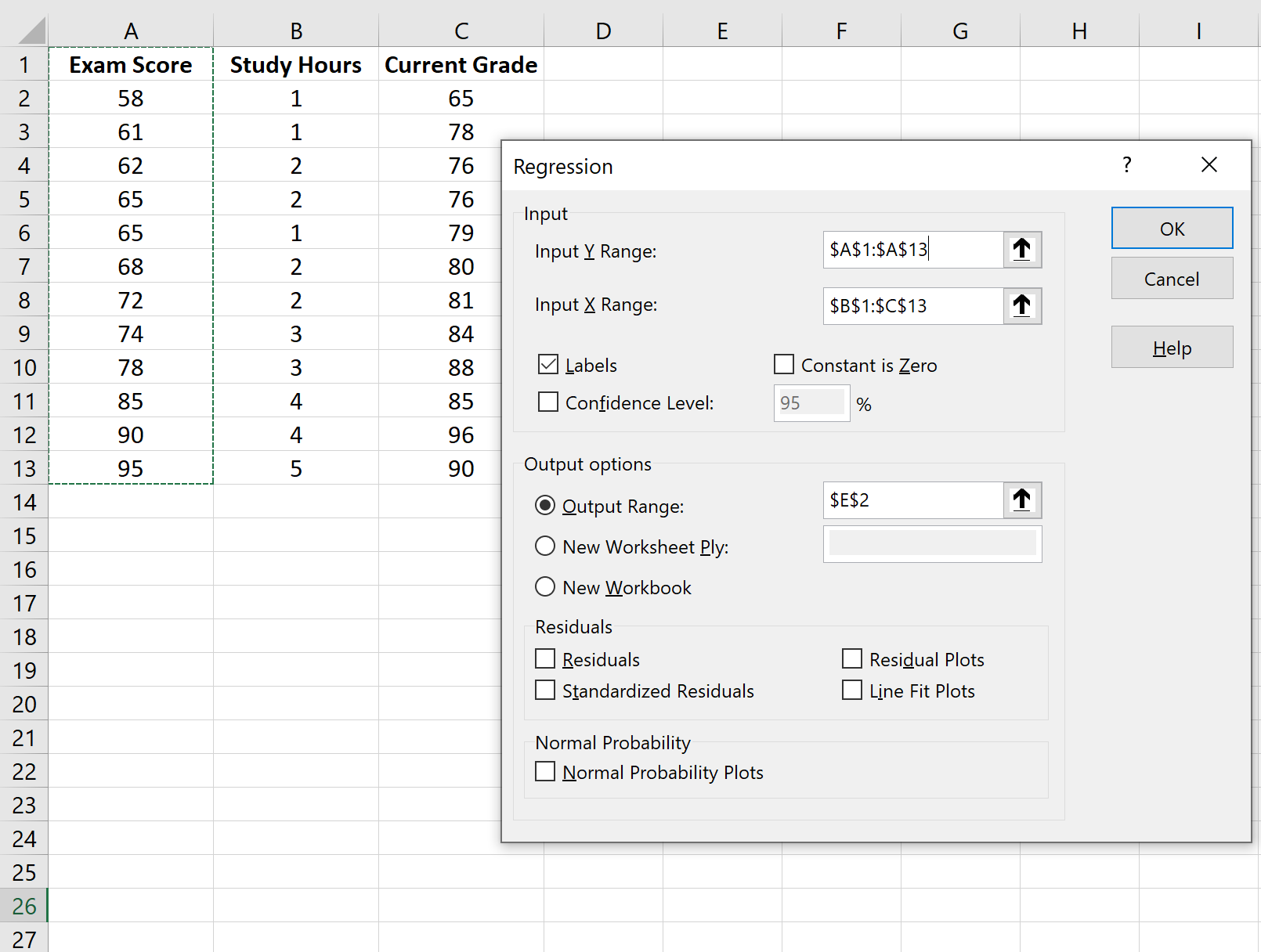
Далі ми підберемо модель множинної лінійної регресії , використовуючи оцінку за іспит як змінну відповіді , а навчальні години та поточну оцінку як змінні-прогнози.

Для цього клацніть вкладку «Дані» на верхній стрічці, а потім клацніть «Аналіз даних» :

Якщо цей параметр недоступний, спочатку потрібно завантажити Data Analysis ToolPak .

У вікні, що з’явиться, виберіть Регресія . У новому вікні, що з’явиться, введіть таку інформацію:

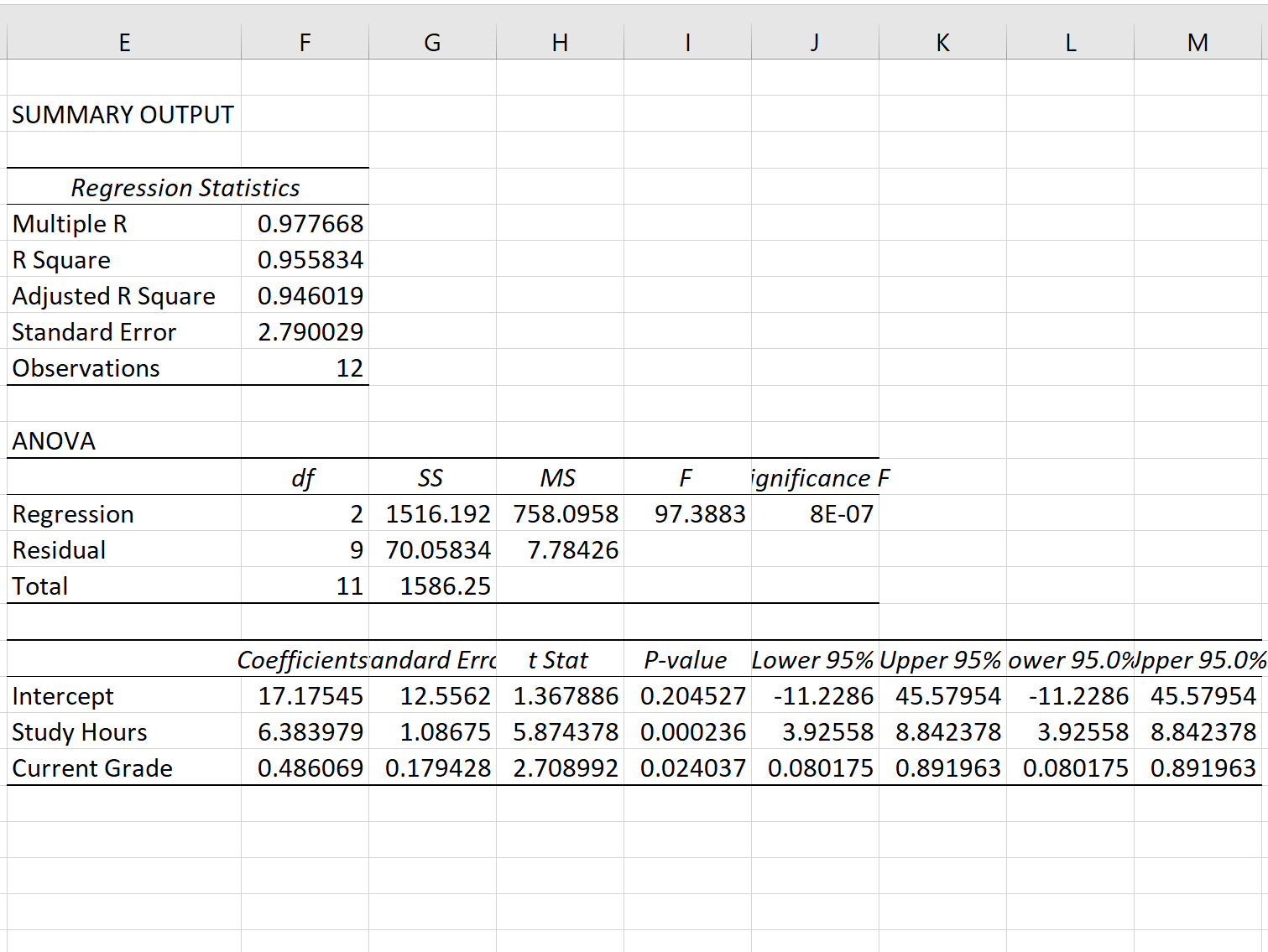
Після натискання кнопки OK з’явиться вихід регресійної моделі:

Крок 3: Інтерпретація стандартної помилки регресії

Стандартна помилка моделі регресії – це число, яке стоїть поруч зі стандартною помилкою :

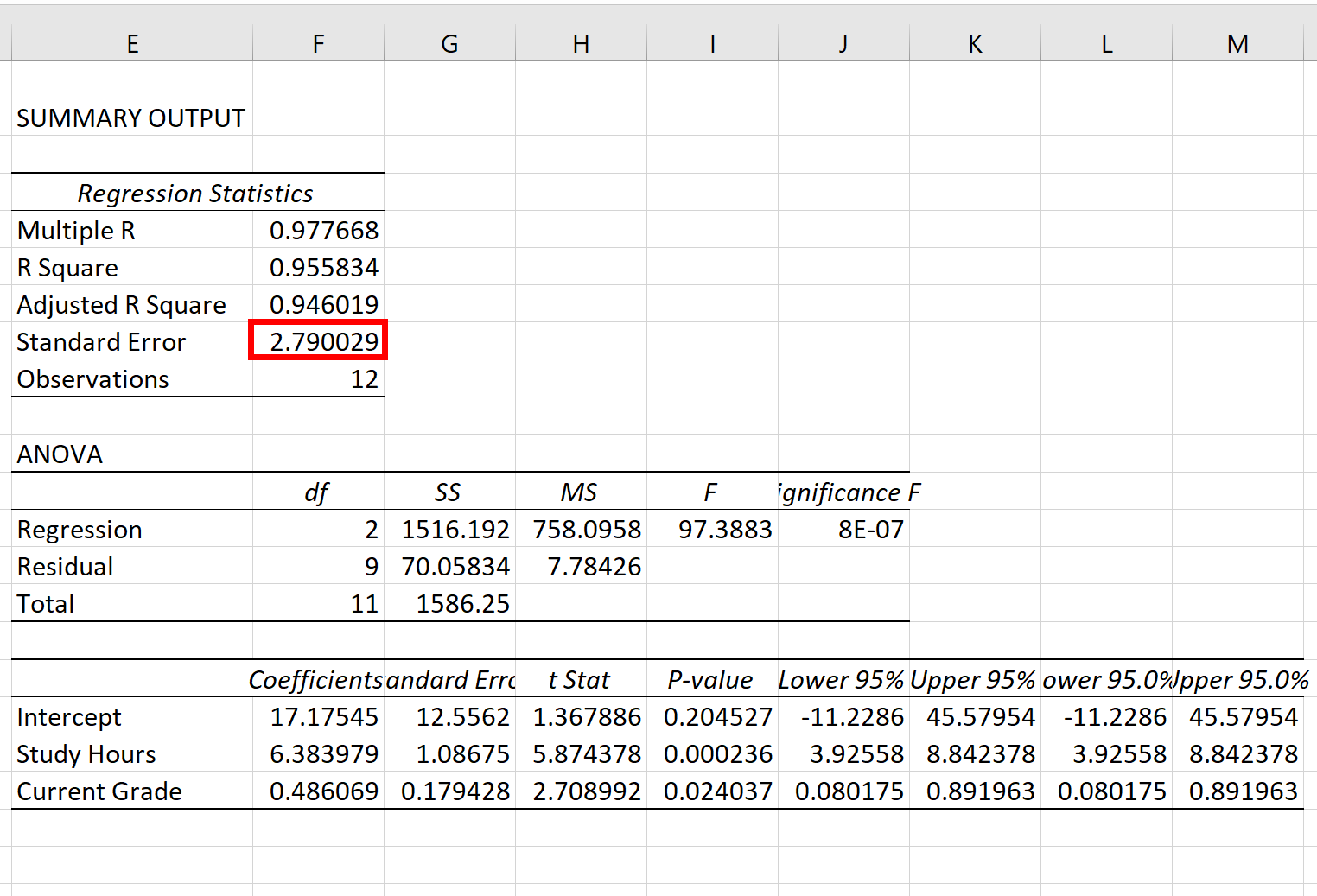
Стандартна помилка цієї моделі регресії дорівнює 2,790029 .

Це число представляє середню відстань між фактичними результатами іспиту та результатами іспиту, передбаченими моделлю.

Зауважте, що результати деяких іспитів будуть більш ніж на 2,79 одиниць від прогнозованого балу, тоді як інші будуть ближчими. Але в середньому відстань між фактичними результатами іспиту та прогнозованими результатами становить 2,790029 .

Також зауважте, що менша стандартна помилка регресії вказує на те, що модель регресії більше відповідає набору даних.

Отже, якщо ми адаптуємо нову регресійну модель до набору даних і отримаємо стандартну помилку, скажімо, 4,53 , ця нова модель буде менш ефективною для прогнозування результатів іспитів, ніж попередня модель.

Додаткові ресурси

Іншим поширеним способом вимірювання точності регресійної моделі є використання R-квадрату. Перегляньте цю статтю , щоб отримати гарне пояснення переваг використання стандартної помилки регресії для вимірювання точності порівняно з R-квадратом.