Excel: обчисліть стандартне відхилення частотного розподілу
Часто вам може знадобитися обчислити стандартне відхилення частотного розподілу в Excel.
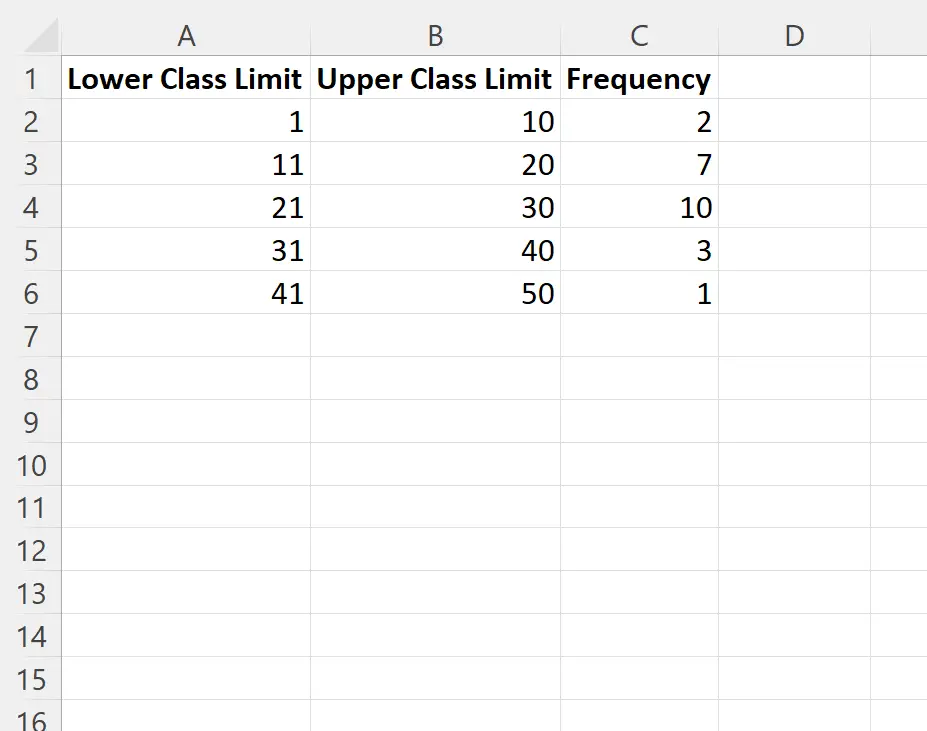
Наприклад, припустімо, що у вас такий розподіл частот:
У наступному покроковому прикладі показано, як обчислити стандартне відхилення цього розподілу частот у Excel.
Крок 1: Введіть значення для розподілу частот
Спочатку ми введемо обмеження класу та значення частоти для нашого розподілу частот:

Крок 2: обчисліть середнє значення частотного розподілу
Ми можемо використати таку формулу, щоб оцінити середнє значення нашого розподілу частот:
Середнє значення: Σm i n i / N
золото:
- mi : середина i- ї групи
- n i : частота i- ї групи
- N: Загальний розмір вибірки
Щоб застосувати цю формулу в Excel, ми введемо такі формули в клітинки D2 , E2 і F2 :
- D2 : =СЕРЕДНЄ (A2:B2)
- E2 : =D2*C2
- F2 : =SUM($E$2:$E$6)/SUM($C$2:$C$6)
Потім ми клацнемо й перетягнемо ці формули до кожної клітинки, що залишилася в кожному стовпці:
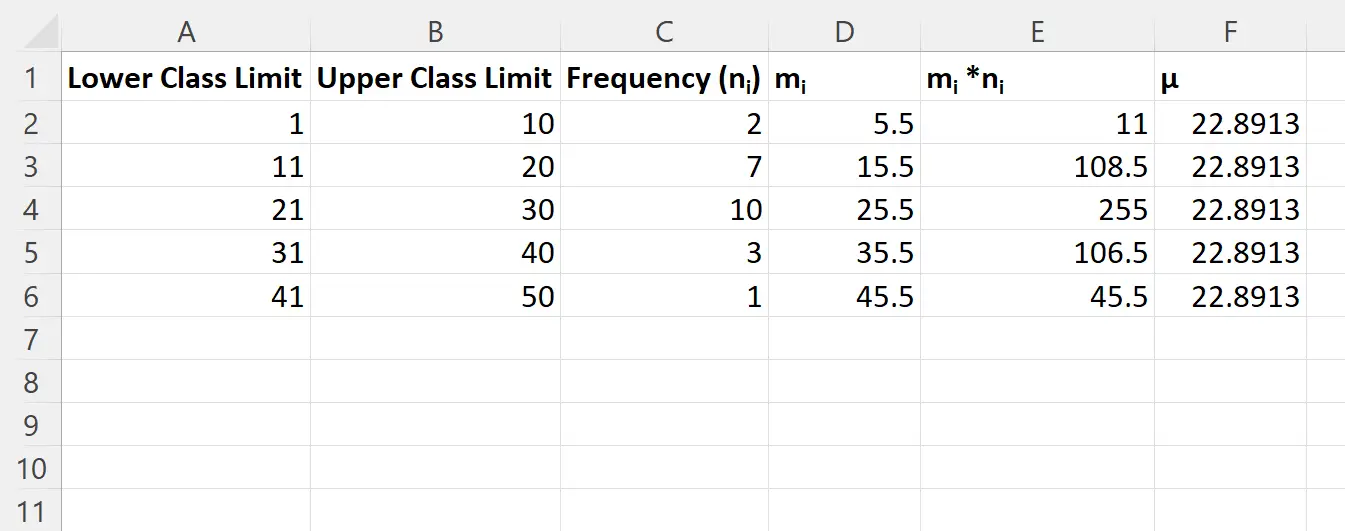
Крок 3: Обчисліть стандартне відхилення частотного розподілу
Ми можемо використати таку формулу, щоб оцінити стандартне відхилення нашого розподілу частот:
Стандартне відхилення: √ Σn i (m i -μ) 2 / (N-1)
золото:
- n i : частота i- ї групи
- mi : середина i- ї групи
- μ : середнє значення
- N: Загальний розмір вибірки
Щоб застосувати цю формулу в Excel, ми введемо такі формули в клітинки G2 , H2 та I2 :
- G2 : =D2-F2
- H2 : =G2^2
- I2 : =C2*H2
Потім ми клацнемо й перетягнемо ці формули до кожної клітинки, що залишилася в кожному стовпці:
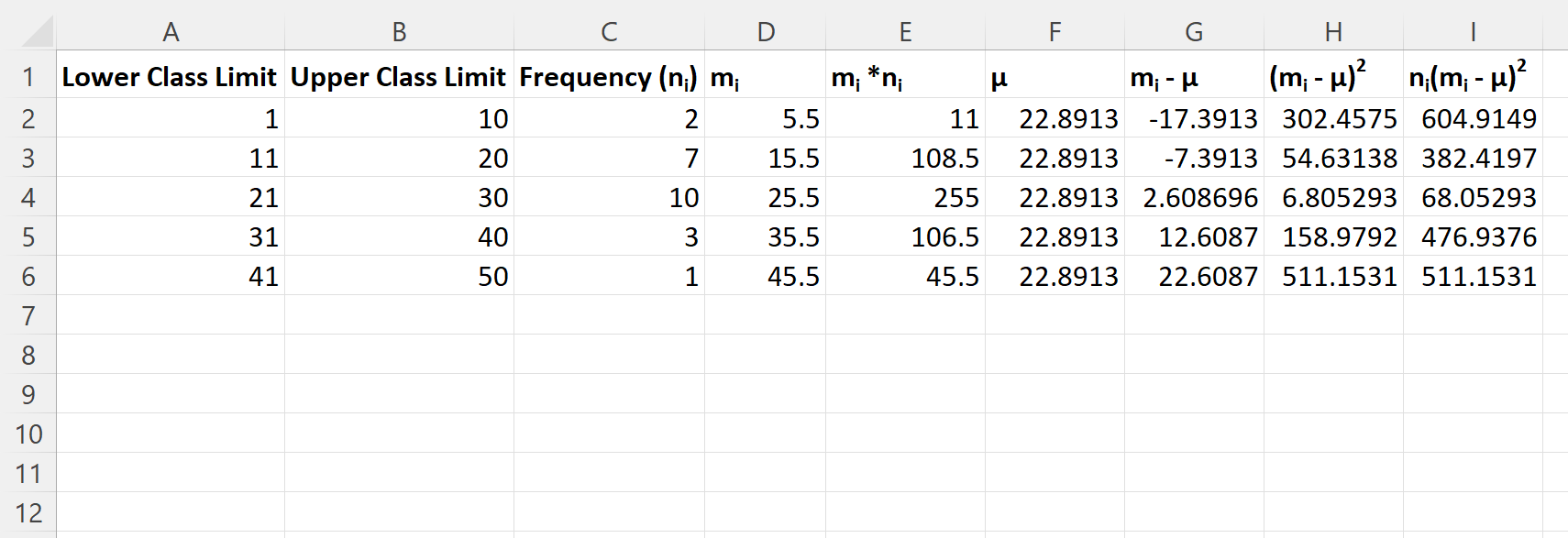
Нарешті, ми можемо ввести таку формулу в клітинку B8 , щоб обчислити стандартне відхилення цього розподілу частот:
=SQRT(SUM( I2:I6 )/(SUM( C2:C6 )-1))
На наступному знімку екрана показано, як використовувати цю формулу на практиці:
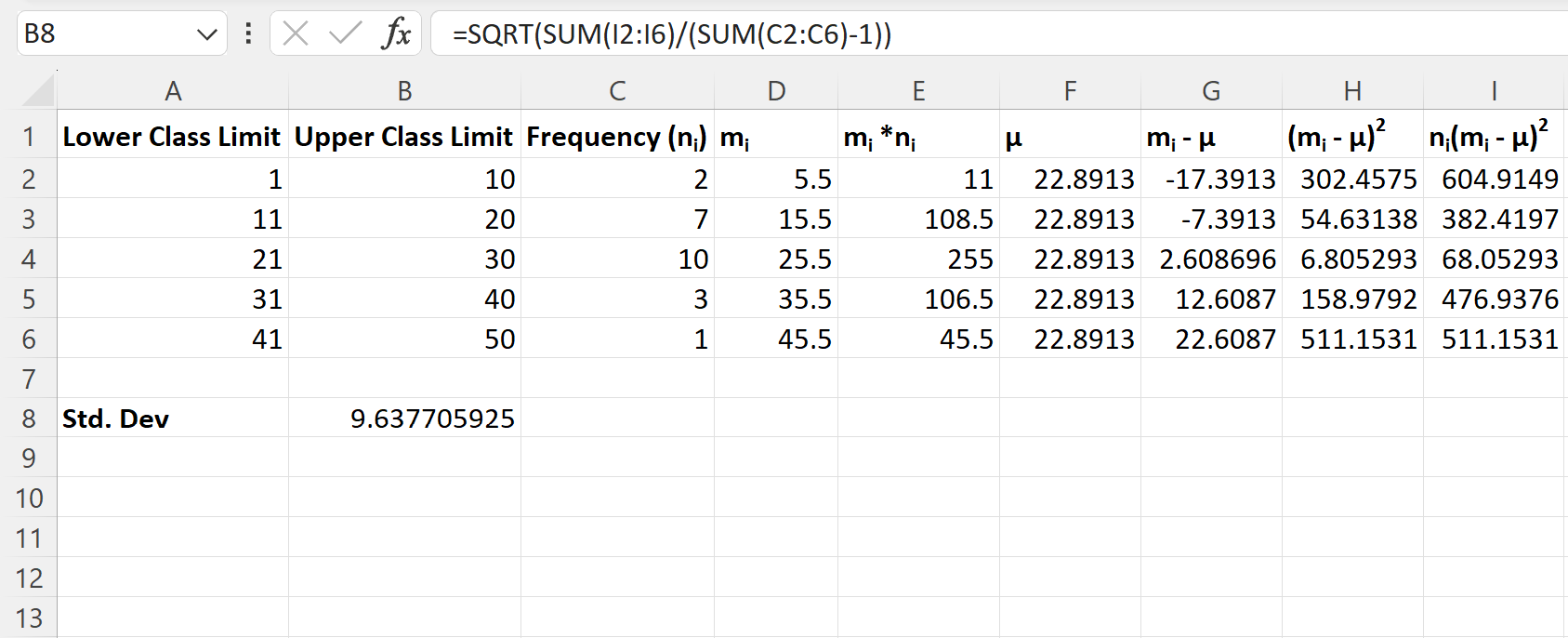
Стандартне відхилення цього розподілу частоти дорівнює 9,6377 .
Додаткові ресурси
У наступних посібниках пояснюється, як виконувати інші типові завдання в Excel:
Як створити кластерний розподіл частот у Excel
Як створити процентний розподіл частоти в Excel
Як обчислити кумулятивну частоту в Excel