Як виконати квадратичну регресію в stata
Коли дві змінні мають лінійний зв’язок, ви часто можете використовувати просту лінійну регресію , щоб кількісно визначити їхній зв’язок.

Однак, коли дві змінні мають квадратичний зв’язок, ви можете використовувати квадратичну регресію , щоб кількісно визначити їхній зв’язок.

Цей підручник пояснює, як виконати квадратичну регресію в Stata.
Приклад: квадратична регресія в Stata
Припустімо, ми хочемо зрозуміти залежність між кількістю відпрацьованих годин і щастям. У нас є такі дані про кількість відпрацьованих годин на тиждень і рівень щастя (за шкалою від 0 до 100) для 16 різних людей:
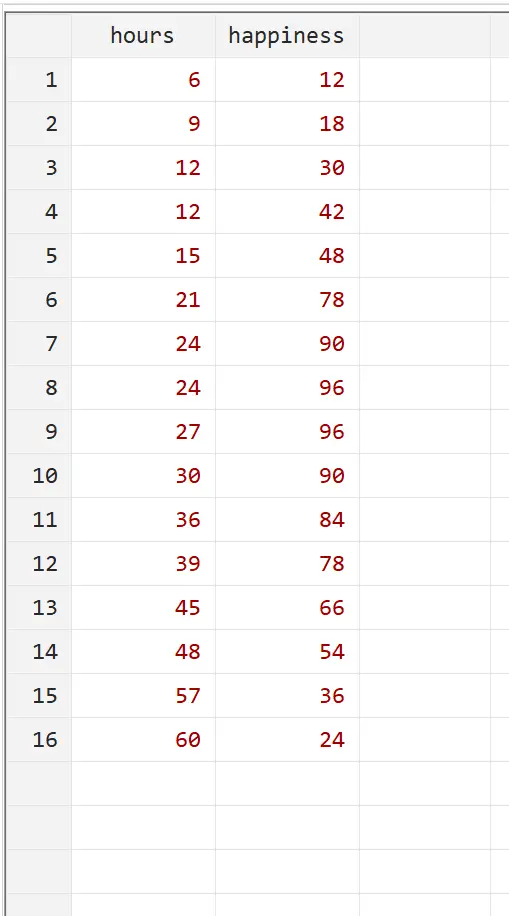
Ви можете відтворити цей приклад, ввівши ці точні дані в Stata за допомогою Дані > Редактор даних > Редактор даних (Редагувати) у верхньому меню.
Виконайте наступні кроки, щоб виконати квадратичну регресію в Stata.
Крок 1: Візуалізуйте дані.
Перш ніж ми зможемо використовувати квадратичну регресію, ми повинні переконатися, що зв’язок між пояснювальною змінною (годинами) і змінною відповіді (щастям) дійсно є квадратичною. Отже, давайте візуалізуємо дані за допомогою діаграми розсіювання , ввівши наступне у полі команди:
розганяти години щастя
Це створює таку діаграму розсіювання:
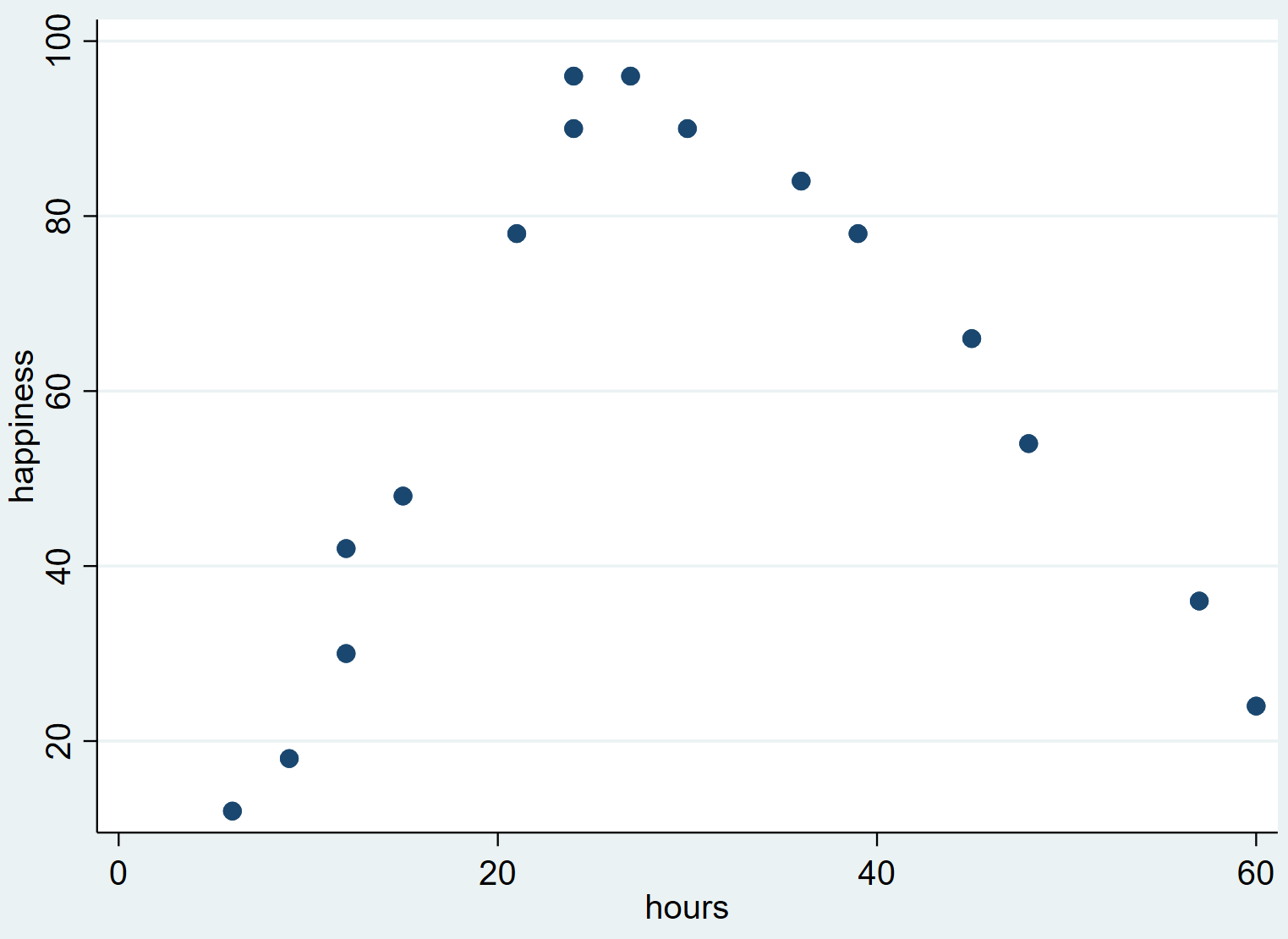
Ми бачимо, що щастя має тенденцію до зростання, коли кількість відпрацьованих годин збільшується від нуля до певної точки, але потім починає зменшуватися, коли кількість відпрацьованих годин перевищує приблизно 30.
Ця перевернута буква «U» на діаграмі розсіювання вказує на те, що існує квадратична залежність між відпрацьованими годинами та щастям, що означає, що ми повинні використовувати квадратичну регресію для кількісної оцінки цієї залежності.
Крок 2: Виконайте квадратичну регресію.
Перш ніж пристосувати модель квадратичної регресії до даних, нам потрібно створити нову змінну для квадратичних значень нашої змінної прогнозу годин . Ми можемо зробити це, ввівши наступне в поле команди:
gen hours2 = години*години
Ми можемо переглянути цю нову змінну, перейшовши в Дані > Редактор даних > Редактор даних (Огляд) у верхньому меню.
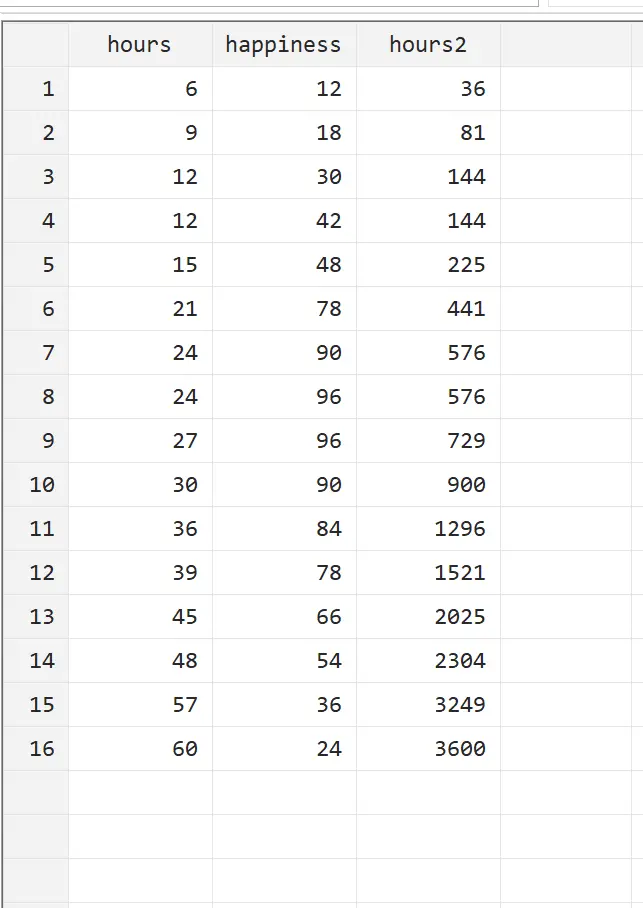
Ми бачимо, що години2 — це просто години в квадраті. Тепер ми можемо виконати квадратичну регресію, використовуючи години та години2 як пояснювальні змінні та щастя як змінну відповіді. Щоб виконати квадратичну регресію, введіть наступне у полі команди:
години регресу години щастя2
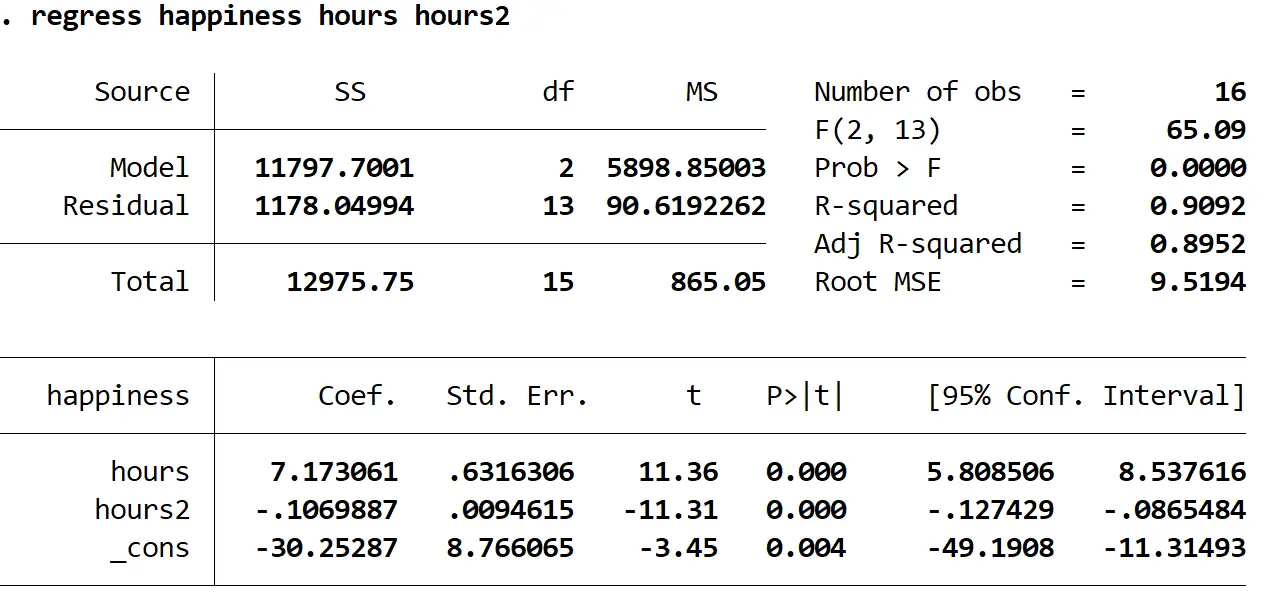
Ось як інтерпретувати найцікавіші числа в результаті:
Імовірність > F: 0,000. Це p-значення для загальної регресії. Оскільки це значення менше 0,05, це означає, що змінні предикторів години та години 2 разом мають статистично значущий зв’язок із змінною відповіді щастя .
R у квадраті: 0,9092. Це частка дисперсії у змінній відповіді, яку можна пояснити пояснювальною змінною. У цьому прикладі 90,92% варіації щастя можна пояснити годинами та годинами 2 .
Рівняння регресії: ми можемо сформувати рівняння регресії, використовуючи значення коефіцієнтів, наведені у вихідній таблиці. У цьому випадку рівняння буде таким:
прогнозоване щастя = -30,25287 + 7,173061 (годин) – 0,1069887 ( 2 години)
Ми можемо використовувати це рівняння, щоб знайти прогнозоване щастя людини, враховуючи кількість годин, які вони працюють на тиждень.
Наприклад, людина, яка працює 60 годин на тиждень, повинна мати рівень щастя 14,97:
прогнозоване щастя = -30,25287 + 7,173061(60) – 0,1069887(60 2 ) = 14,97 .
І навпаки, людина, яка працює 30 годин на тиждень, повинна мати рівень щастя 88,65:
прогнозоване щастя = -30,25287 + 7,173061(30) – 0,1069887(30 2 ) = 88,65 .
Крок 3: Повідомте про результати.
Нарешті, ми хочемо повідомити про результати нашої квадратичної регресії. Ось приклад того, як це зробити:
Було проведено квадратичну регресію, щоб кількісно визначити зв’язок між кількістю годин, які людина працювала, та її відповідним рівнем щастя (вимірюється від 0 до 100). Для аналізу була використана вибірка з 16 осіб.
Результати показали, що існує статистично значущий зв’язок між пояснювальними змінними години та години 2 та змінною відповіді щастя (F(2, 13) = 65,09, p < 0,0001).
Разом ці дві пояснювальні змінні становлять 90,92% поясненої мінливості щастя.
Рівняння регресії вийшло таким:
прогнозоване щастя = -30,25287 + 7,173061 (годин) – 0,1069887 ( 2 години)