Що таке помилка передбачення в статистиці? (визначення та приклади)

У статистиці помилка передбачення відноситься до різниці між значеннями, передбаченими певними моделями, і фактичними значеннями.

Помилка передбачення часто використовується в двох контекстах:

1. Лінійна регресія: використовується для прогнозування значення безперервної змінної відповіді.

Зазвичай ми вимірюємо похибку передбачення моделі лінійної регресії за допомогою метрики, відомої як RMSE , що означає середньоквадратичну помилку.

Він розраховується таким чином:

RMSE = √ Σ(ŷ _i – y _i ) ² / n

золото:

• Σ – символ, що означає «сума»
• ŷ _i – прогнозоване значення для i- ^го спостереження
• y _i – спостережуване значення для ^i-го спостереження
• n – розмір вибірки

2. Логістична регресія: використовується для прогнозування значення двійкової змінної відповіді.

Поширеним способом вимірювання похибки передбачення моделі логістичної регресії є використання метрики, відомої як загальна частота помилок класифікації.

Він розраховується таким чином:

Загальний коефіцієнт неправильної класифікації = (# неправильних прогнозів / # загальних прогнозів)

Чим нижче значення коефіцієнта неправильної класифікації, тим краще модель здатна передбачити результати змінної відповіді.

У наведених нижче прикладах показано, як на практиці обчислити похибку передбачення для моделі лінійної регресії та моделі логістичної регресії.

Приклад 1: обчислення похибки передбачення в лінійній регресії

Припустімо, ми використовуємо регресійну модель, щоб передбачити, скільки очок наберуть 10 гравців у баскетбольній грі.

У наведеній нижче таблиці наведено очки, передбачені моделлю, у порівнянні з фактичними очками, набраними гравцями:

Ми б обчислили середню квадратичну помилку (RMSE) наступним чином:

• RMSE = √ Σ(ŷ _i – y _i ) ² / n
• RMSE = √(((14-12) ² +(15-15) ² +(18-20) ² +(19-16) ² +(25-20) ² +(18-19) ² +(12- 16) ² +(12-20) ² +(15-16) ² +(22-16) ² ) / 10)
• RMSE = 4

Середня квадратична помилка дорівнює 4. Це говорить нам про те, що середнє відхилення між прогнозованими набраними балами та фактичними набраними балами дорівнює 4.

За темою: що вважається хорошим значенням RMSE?

Приклад 2: обчислення похибки передбачення в логістичній регресії

Припустімо, що ми використовуємо логістичну регресійну модель, щоб передбачити, чи будуть задрафтовані 10 студентських баскетболістів у НБА.

У наведеній нижче таблиці показано прогнозований результат для кожного гравця у порівнянні з фактичним результатом (1 = задрафтований, 0 = не задрафтований):

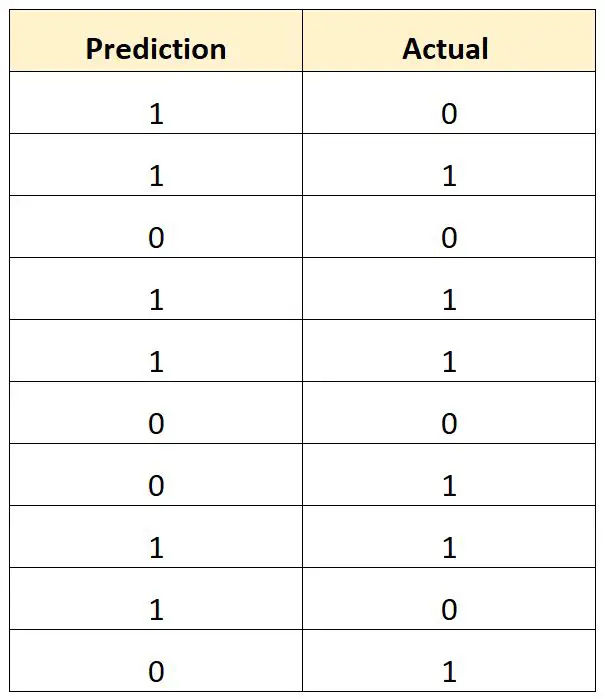
Ми б розрахували загальний рівень неправильної класифікації таким чином:

• Загальний коефіцієнт неправильної класифікації = (# неправильних прогнозів / # загальних прогнозів)
• Загальний рівень помилок класифікації = 4/10
• Загальний рівень неправильної класифікації = 40%

Загальний рівень помилок класифікації становить 40% .

Це значення досить високе, що вказує на те, що модель не дуже добре прогнозує, чи буде гравець обраний чи ні.

Додаткові ресурси

Наступні навчальні посібники містять вступ до різних типів методів регресії:

Вступ до простої лінійної регресії
Вступ до множинної лінійної регресії
Вступ до логістичної регресії