Як створити нормальний розподіл у python (з прикладами)
Ви можете швидко створити нормальний розподіл у Python за допомогою функції numpy.random.normal() , яка використовує такий синтаксис:
numpy. random . normal (loc=0.0, scale=1.0, size=None)
золото:
- loc: Середнє значення розподілу. Значення за замовчуванням 0.
- масштаб: стандартне відхилення розподілу. Значення за умовчанням — 1.
- розмір: розмір вибірки.
Цей підручник показує приклад використання цієї функції для створення звичайного розподілу в Python.
Пов’язане: Як створити дзвоноподібну криву в Python
Приклад: створення нормального розподілу в Python
Наступний код показує, як створити звичайний розподіл у Python:
from numpy. random import seed
from numpy. random import normal
#make this example reproducible
seed(1)
#generate sample of 200 values that follow a normal distribution
data = normal (loc=0, scale=1, size=200)
#view first six values
data[0:5]
array([ 1.62434536, -0.61175641, -0.52817175, -1.07296862, 0.86540763])
Ми можемо швидко знайти середнє значення та стандартне відхилення цього розподілу:
import numpy as np
#find mean of sample
n.p. mean (data)
0.1066888148479486
#find standard deviation of sample
n.p. std (data, ddof= 1 )
0.9123296653173484
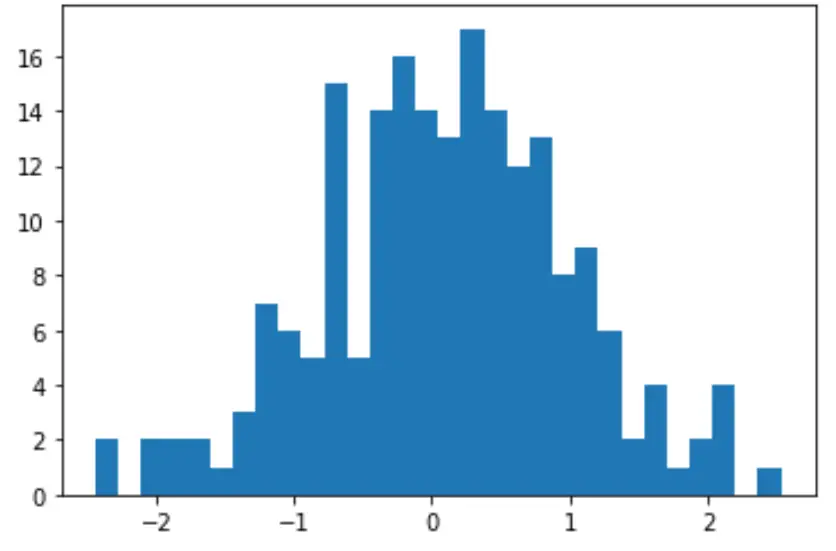
Ми також можемо створити швидку гістограму для візуалізації розподілу значень даних:
import matplotlib. pyplot as plt
count, bins, ignored = plt. hist (data, 30)
plt. show ()
Ми навіть можемо виконати тест Шапіро-Вілка, щоб перевірити, чи походить набір даних із нормальної популяції:
from scipy. stats import shapiro
#perform Shapiro-Wilk test
shapiro(data)
ShapiroResult(statistic=0.9958659410, pvalue=0.8669294714)
P-значення тесту виявляється рівним 0,8669 . Оскільки це значення не менше 0,05, ми можемо припустити, що дані вибірки надходять із нормально розподіленої сукупності.
Цей результат не повинен дивувати, оскільки ми генерували дані за допомогою функції numpy.random.normal() , яка генерує випадкову вибірку даних із нормального розподілу.