Як виконати тест хі-квадрат вручну (крок за кроком)

Тест відповідності хі-квадрат використовується для визначення того, чи відповідає категоріальна змінна гіпотетичному розподілу.

У наведеному нижче покроковому прикладі показано, як вручну виконати тест на відповідність хі-квадрат.

Перевірка відповідності хі-квадрат вручну

Припустимо, ми вважаємо, що певний кубик правильний. Іншими словами, ми вважаємо, що кубики мають однакову ймовірність потрапити на 1, 2, 3, 4, 5 або 6 під час даного кидка.

Щоб перевірити це, ми кидаємо його 60 разів і кожного разу записуємо число, на яке воно потрапляє. Результати такі:

• 1 :8 разів
• 2 : 12 разів
• 3 : 18 разів
• 4 :9 разів
• 5 :7 разів
• 6 :6 разів

Виконайте наступні кроки, щоб виконати тест відповідності хі-квадрат, щоб визначити, чи справедливі кубики.

Крок 1: Визначте нульову та альтернативну гіпотези

• H ₀ (нуль): кубики мають однакову ймовірність випадіння для кожного числа.
• H ₁ (альтернатива): Гральні кістки не мають однакової ймовірності випадіння для кожного числа.

Крок 2: Обчисліть спостережувану та очікувану частоти

Далі створимо таблицю спостережуваних і очікуваних частот для кожного числа на кубику:

Примітка . Якщо ми вважаємо кубик справедливим, це означає, що ми очікуємо, що він впаде на кожне число однакову кількість разів – у цьому випадку 10 разів на кожне.

Крок 3: Обчисліть статистику тесту

Статистичний показник хі-квадрат, X ² , обчислюється таким чином:

• X ² = Σ(OE) ² / E

У наведеній нижче таблиці показано, як розрахувати цю тестову статистику:

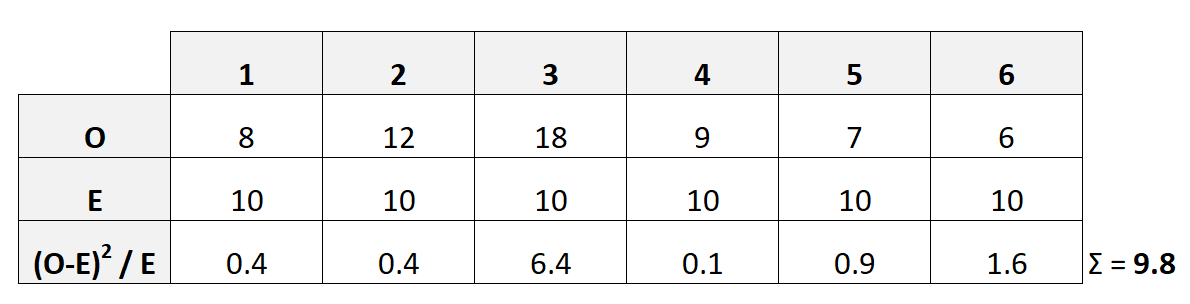
У цьому випадку X ² виявляється рівним 9,8 .

Крок 4: Знайдіть критичне значення

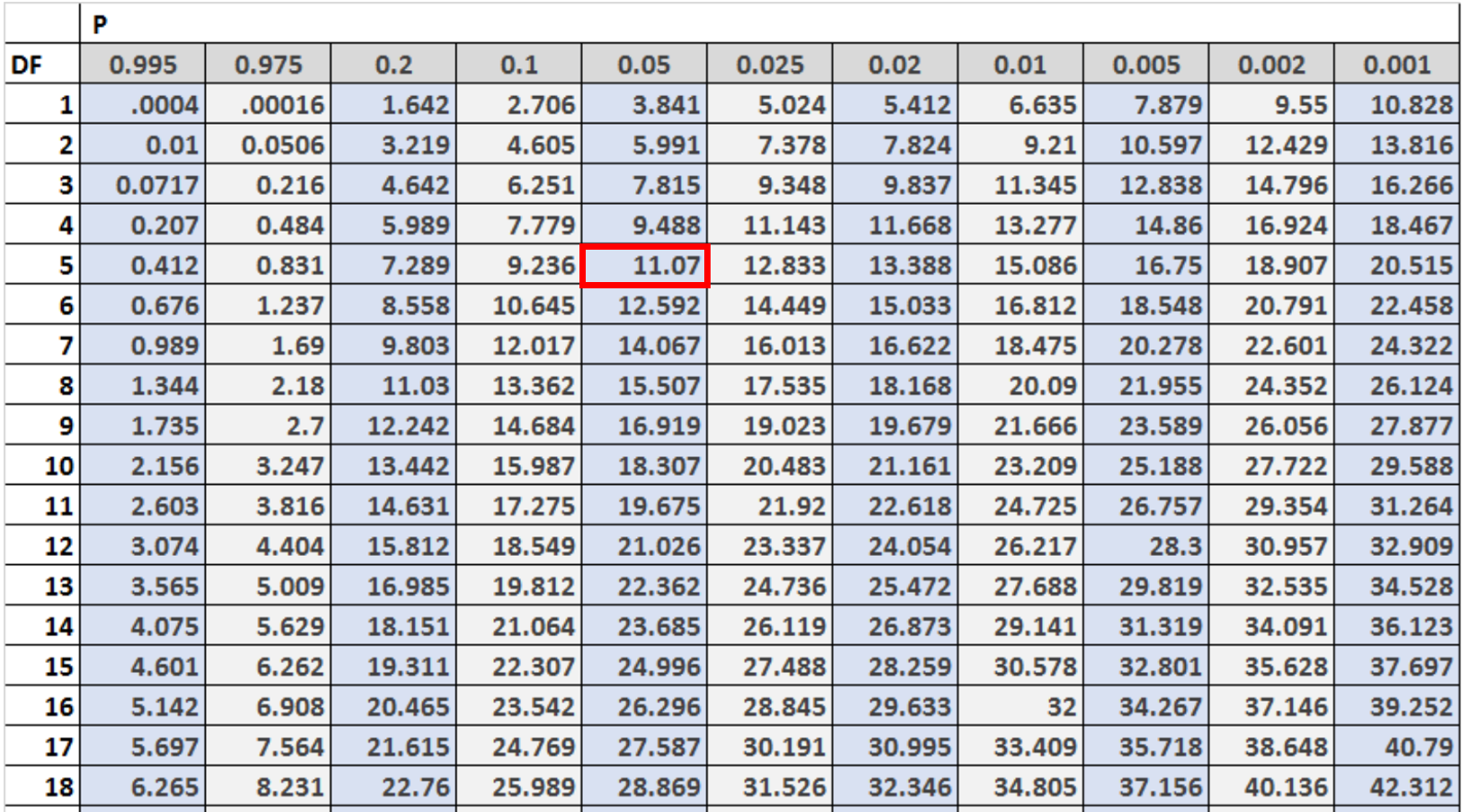
Далі нам потрібно знайти критичне значення в таблиці розподілу хі-квадрат, яке відповідає α = 0,05 і df = (#категорії – 1).

У цьому випадку є 6 категорій, тому ми будемо використовувати df = 6 – 1 = 5 .

Ми бачимо, що критичне значення становить 11,07 .

Крок 5: Відкинути або не відхилити нульову гіпотезу

Оскільки наша тестова статистика менша за критичне значення, ми не можемо відхилити нульову гіпотезу. Це означає, що у нас недостатньо доказів, щоб стверджувати, що кості несправедливі.

Додаткові ресурси

Наступні ресурси пропонують додаткову інформацію про тест відповідності хі-квадрат:

Вступ до тесту відповідності хі-квадрат
Як виконати тест на відповідність хі-квадрат у R
Калькулятор тесту відповідності хі-квадрат