Т-критерій стьюдента

за Редакція 3 Серпня, 2023 Статистика 0 коментарів

У цій статті пояснюється, що таке t-критерій Стьюдента та для чого він використовується в статистиці. Таким чином, ви дізнаєтеся, як виконується критерій Стьюдента, які існують різні типи критеріїв Стьюдента та формула для кожного.

Що таке t-критерій Стьюдента?

Т-тест Стьюдента , також званий Т-тестом або просто t-тестом , є статистичним тестом, у якому тестова статистика відповідає t-розподілу Стьюдента . Тому в статистиці t-критерій Стьюдента використовується для відхилення або прийняття нульової гіпотези перевірки гіпотези.

Зокрема, t-критерій Стьюдента використовується для перевірки гіпотез , у яких сукупність, що вивчається, має нормальний розподіл, але розмір вибірки надто малий, щоб знати дисперсію сукупності.

Коротше кажучи, t-критерій Стьюдента використовується для відхилення або прийняття гіпотези дослідження певних перевірок гіпотез. Наприклад, t-критерій Стьюдента використовується для перевірки гіпотез для однієї вибірки, для незалежних вибірок або для пов’язаних вибірок. Далі ми побачимо, як обчислюється критерій Стьюдента в кожному випадку.

Типи t-критеріїв Стьюдента

Існує три типи критеріїв Стьюдента :

Одновибірковий t-критерій Стьюдента – використовується для перевірки гіпотези про значення вибіркового середнього.
Критерій Стьюдента для двох незалежних вибірок : він дозволяє перевірити гіпотезу щодо різниці між середніми двома незалежними вибірками.
Т-критерій Стьюдента для двох парних вибірок (або пов’язаних вибірок) – використовується для дослідження гіпотези про середнє значення вибірки, перевіреної двічі.

Зразок критерію Стьюдента

Перевірки гіпотез для вибіркового середнього – це ті, в яких нульова гіпотеза та альтернативна гіпотеза тесту говорять щось про значення середнього сукупності.

Формула t-критерію Стьюдента для однієї вибірки виглядає наступним чином:

$\displaystyle t=\frac{\overline{x}-\mu}{\displaystyle \frac{s}{\sqrt{n}}}$

золото:

$t$

це статистика перевірки гіпотези для середнього значення, яке визначається t-розподілом Стьюдента.
$\overline{x}$

це зразок засобів.
$\mu$

це значення середнього, запропоноване в перевірці гіпотези.
$s$

є стандартним відхиленням вибірки.
$n$

це розмір вибірки.

Після того, як значення критерію Стьюдента було обчислено, результат статистичного тесту з критичним значенням повинен бути інтерпретований, щоб відхилити чи ні нульову гіпотезу:

Якщо перевірка гіпотези для середнього є двосторонньою, нульова гіпотеза відхиляється, якщо абсолютне значення критерію Стьюдента перевищує критичне значення t _α/2|n-1 .
Якщо перевірка гіпотези для середнього збігається з правим хвостом, нульова гіпотеза відхиляється, якщо значення t-критерію Стьюдента перевищує критичне значення t _α|n-1 .
Якщо перевірка гіпотези для середнього збігається з лівим хвостом, нульова гіпотеза відхиляється, якщо значення t-критерію Стьюдента менше критичного значення -t _α|n-1 .

$\begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |t|>t_{\alpha/2|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t>t_{\alpha|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t<-t_{\alpha|n-1} \text{ se rechaza } H_0\end{array}$

Зверніть увагу, що критичні тестові значення отримані з таблиці розподілу Стьюдента.

➤ Див.: Конкретний приклад перевірки гіпотези для середнього

Критерій Стьюдента для незалежних вибірок

Т-критерій Стьюдента для незалежних вибірок використовується, щоб відхилити або прийняти гіпотезу про взаємозв’язок між середніми двома сукупностями, наприклад, що середні дві сукупності різні або що середнє значення сукупності А більше, ніж середнє . населення Б.

Однак у цьому випадку формула t-критерію Стьюдента змінюється залежно від того, чи можна вважати дисперсії сукупності рівними чи ні. Тоді ми побачимо два можливі випадки.

Невідомі та рівні відхилення

Формула для обчислення t-критерію Стьюдента для незалежних вибірок, коли дисперсії сукупності невідомі, але вважаються рівними, виглядає наступним чином:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

золото:

$t$

це статистика перевірки гіпотези для різниці середніх із невідомими дисперсіями, яка відповідає t-розподілу Стьюдента з n ₁ + n ₂ -2 ступенями свободи.
$\mu_1$

це середнє значення сукупності 1.
$\mu_2$

це середнє значення сукупності 2.
$\overline{x_1}$

є середнім значенням зразка 1.
$\overline{x_2}$

є середнім значенням зразка 2.
$s_p$

є зведеним стандартним відхиленням.
$n_1$

розмір вибірки 1.
$n_2$

розмір вибірки 2.

Сукупне стандартне відхилення двох зразків обчислюється за такою формулою:

$\displaystyle s_p=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}$

Невідомі та різні варіації

Коли дисперсії генеральної сукупності невідомі і, крім того, вважаються різними, формула для розрахунку критерію Стьюдента для незалежних вибірок виглядає наступним чином:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}$

золото:

$t$

це статистика перевірки гіпотези для різниці середніх значень з невідомими дисперсіями, яка відповідає t-розподілу Стьюдента.
$\mu_1$

це середнє значення сукупності 1.
$\mu_2$

це середнє значення сукупності 2.
$\overline{x_1}$

є середнім значенням зразка 1.
$\overline{x_2}$

є середнім значенням зразка 2.
$\sigma_1$

є стандартним відхиленням сукупності 1.
$\sigma_2$

є стандартним відхиленням сукупності 2.
$n_1$

розмір вибірки 1.
$n_2$

розмір вибірки 2.

Однак у цьому випадку ступені вільності t-розподілу Стьюдента розраховуються за такою формулою:

$\displaystyle GL=\frac{\displaystyle\left(\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}\right)^2}{\displaystyle\frac{\displaystyle\frac{s_1^2}{n_1}}{n_1-1}+\frac{\displaystyle\frac{s_2^2}{n_2}}{n_2-1}}$

➤ Див.: Конкретний приклад перевірки гіпотези на різницю середніх

Критерій Стьюдента для парних або пов’язаних вибірок

Цей тест використовується, коли два зразки, що досліджуються, пов’язані один з одним, тож це фактично один зразок індивідуумів, який аналізувався двічі (щоразу за різних умов).

Наприклад, ви можете проаналізувати оцінки студентів з курсу математики та статистики, щоб побачити, чи є значна різниця між середніми значеннями з двох предметів. У цьому випадку оцінка кожного учня з математики пов’язується зі статистичною оцінкою цього самого учня.

Формула t-критерію Стьюдента для парних або пов’язаних зразків виглядає так:

$\displaystyle t=\frac{\overline{x_D}-\mu_D}{\displaystyle \frac{s_D}{\sqrt{n}}}$

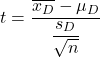
золото:

$t$

це статистика перевірки гіпотези для парних середніх, яка визначається t-розподілом Стьюдента.
$\overline{x_D}$

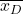
це середнє значення вибірки, утвореної різницею в даних.
$\mu_D$

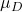
це значення середнього, запропоноване в перевірці гіпотези.
$s_D$

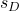
є стандартним відхиленням вибірки, утвореної різницею в даних.
$n$

це розмір вибірки.

Припущення t-критерію Стьюдента

Щоб виконати критерій Стьюдента, мають бути виконані наступні умови:

Безперервність – дані вибірки є безперервними.
Випадковість : зразки даних були відібрані випадковим чином.
Однорідність : Дисперсія вибірки даних є однорідною.
Нормальність – розподіл, який визначає вибірку даних, є приблизно нормальним.

Як виконати тест Стьюдента

Нарешті, у підсумку, детально описано кроки, які необхідно виконати для виконання t-критерію Стьюдента.

Визначте нульову та альтернативну гіпотези перевірки гіпотез.
Встановіть рівень значущості (α) перевірки гіпотези.
Перевірте, чи виконуються припущення критерію Стьюдента.
Застосуйте відповідну формулу t-критерію Стьюдента та обчисліть тестову статистику.
Інтерпретуйте результат критерію Стьюдента, порівнявши його з критичним значенням критерію.

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше

Що таке t-критерій Стьюдента?

Типи t-критеріїв Стьюдента

Зразок критерію Стьюдента

Критерій Стьюдента для незалежних вибірок

Невідомі та рівні відхилення

Невідомі та різні варіації

Критерій Стьюдента для парних або пов’язаних вибірок

Припущення t-критерію Стьюдента

Як виконати тест Стьюдента

Про автора

Редакція

Додати коментар