Як виконати тест kpss на python

Тест KPSS можна використовувати, щоб визначити, чи має часовий ряд стаціонарний тренд.

Цей тест використовує таку нульову та альтернативну гіпотезу:

• H ₀ : часовий ряд має стаціонарний тренд.
• H _A : часовий ряд не має стаціонарного тренду.

Якщо p-значення тесту нижче певного рівня значущості (наприклад, α = 0,05), тоді ми відхиляємо нульову гіпотезу та робимо висновок, що часовий ряд не має стаціонарного тренду.

Інакше ми не зможемо відхилити нульову гіпотезу.

У наступних прикладах показано, як виконати тест KPSS у Python.

Приклад 1: Тест KPSS у Python (зі стаціонарними даними)

По-перше, давайте створимо деякі підроблені дані в Python для роботи:

 import numpy as np
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seed ( 1 )

#create time series data
data = np. random . normal (size= 100 )

#create line plot of time series data
plt. plot (data) 

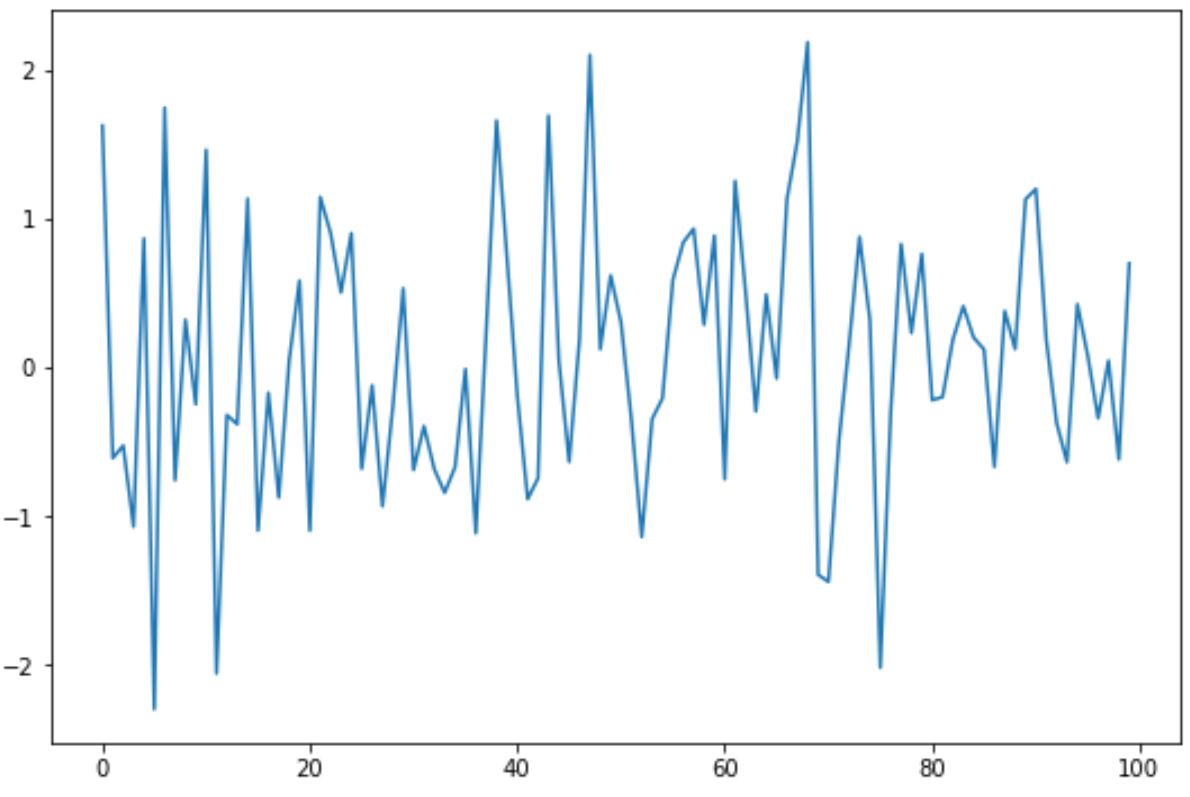
Ми можемо використати функцію kpss() із пакету statsmodels , щоб виконати тест KPSS на даних часового ряду:

 import statsmodels. api as sm

#perform KPSS test
sm. tsa . stattools . kpss (data, regression=' ct ')

(0.0477617848370993,
 0.1,
 1,
 {'10%': 0.119, '5%': 0.146, '2.5%': 0.176, '1%': 0.216})

InterpolationWarning: The test statistic is outside of the range of p-values available
in the look-up table. The actual p-value is greater than the p-value returned.

Ось як інтерпретувати результат:

• Статистика тесту KPSS: 0,04776
• P-значення: 0,1
• Параметр зміщення відсікання: 1
• Критичні значення на 10% , 5% , 2,5% і 1%

P-значення становить 0,1 . Оскільки це значення не менше 0,05, ми не можемо відхилити нульову гіпотезу тесту KPSS.

Це означає, що можна вважати, що часовий ряд має стаціонарний тренд.

Примітка 1 : P-значення фактично все ще перевищує 0,1, але найнижче значення, яке видасть функція kpss(), становить 0,1.

Примітка 2 : Ви повинні використовувати аргумент regression=’ct’ , щоб вказати, що нульова гіпотеза тесту полягає в тому, що дані мають стаціонарну тенденцію.

Приклад 2: Тест KPSS у Python (з нестаціонарними даними)

По-перше, давайте створимо деякі підроблені дані в Python для роботи:

 import numpy as np
import matplotlib. pyplot as plt

#make this example reproducible
n.p. random . seed ( 1 )

#create time series data
data =np. array ([0, 3, 4, 3, 6, 7, 5, 8, 15, 13, 19, 12, 29, 15, 45, 23, 67, 45])

#create line plot of time series data
plt. plot (data) 

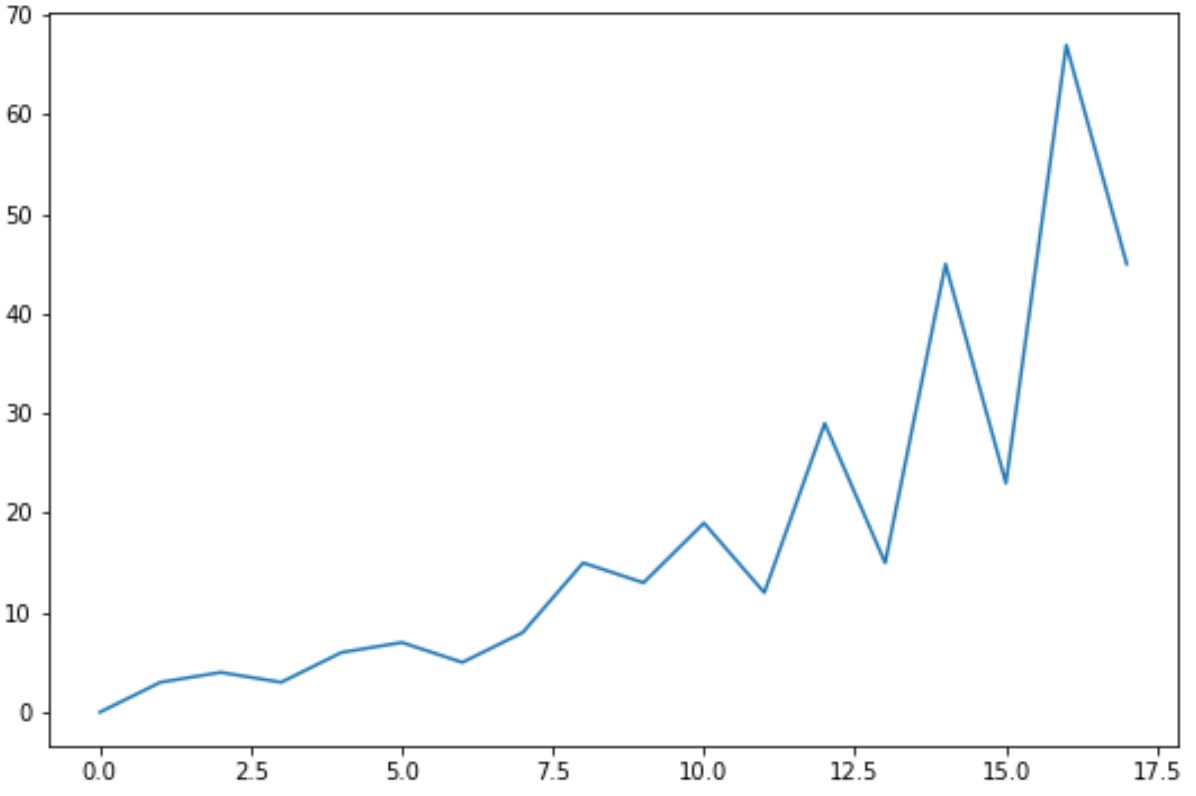
Знову ж таки, ми можемо використати функцію kpss() із пакету statsmodels , щоб виконати тест KPSS на даних часового ряду:

 import statsmodels. api as sm

#perform KPSS test
sm. tsa . stattools . kpss (data, regression=' ct ')

(0.15096358910843685,
 0.04586367574296928,
 3,
 {'10%': 0.119, '5%': 0.146, '2.5%': 0.176, '1%': 0.216})

Ось як інтерпретувати результат:

• Статистика тесту KPSS: 0,1509
• P-значення: 0,0458
• Параметр зміщення відсікання: 3
• Критичні значення на 10% , 5% , 2,5% і 1%

P-значення становить 0,0458 . Оскільки це значення менше 0,05, ми відхиляємо нульову гіпотезу тесту KPSS.

Це означає, що часовий ряд не є стаціонарним.

Примітка : ви можете знайти повну документацію для функції kpss() у пакеті statsmodels тут .

Додаткові ресурси

У наступних посібниках надається додаткова інформація про те, як працювати з даними часових рядів у Python:

Як виконати розширений тест Дікі-Фуллера в Python
Як виконати тест тенденції Манна-Кендалла в Python
Як побудувати часовий ряд у Matplotlib