Що таке унімодальний розподіл? (визначення & #038; приклад)

Унімодальний розподіл — це розподіл ймовірностей із чітким піком.

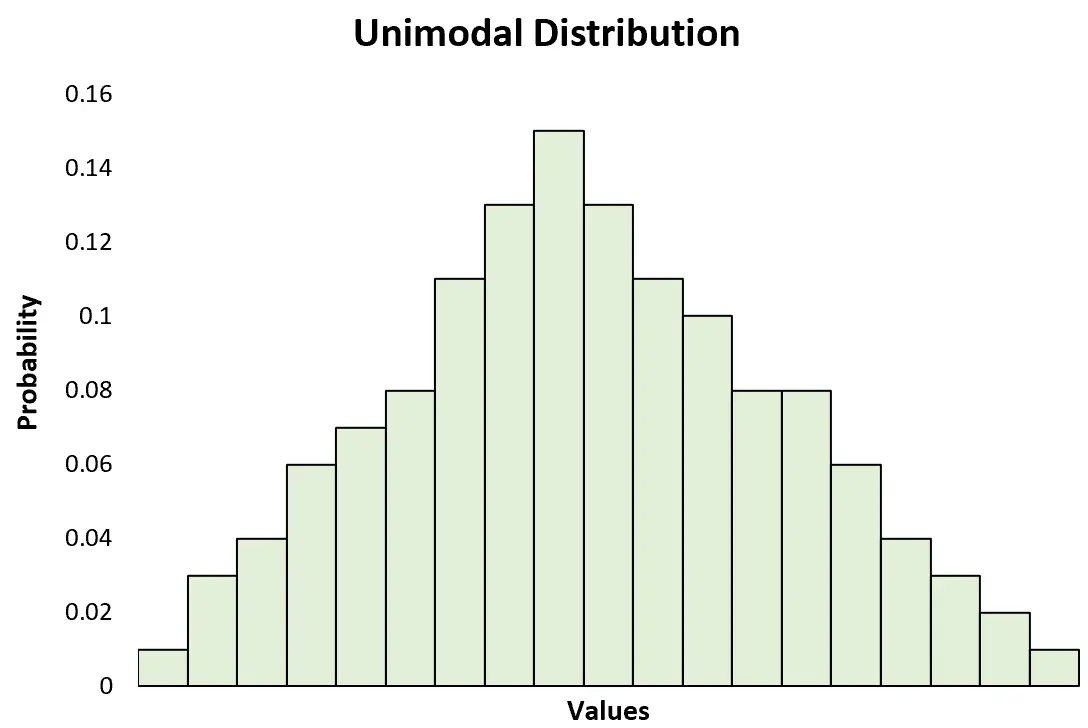
Це контрастує з бімодальним розподілом , який має два чітких піки:

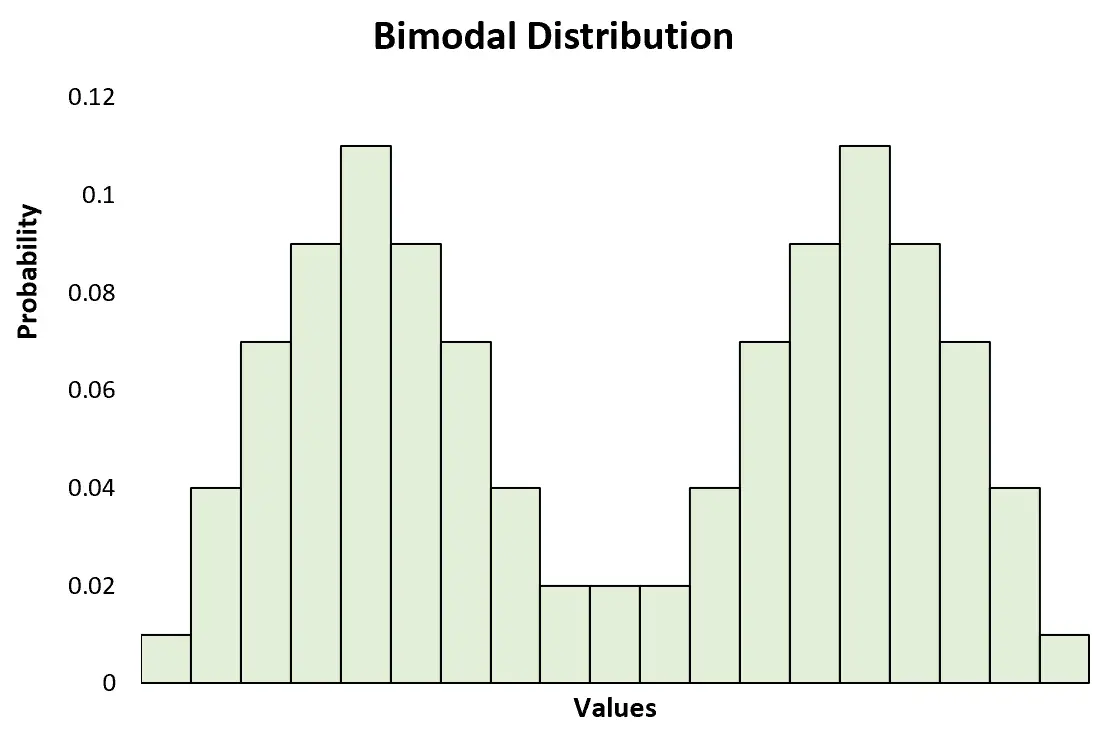
Це також контрастує з мультимодальним розподілом , який має два або більше піків:

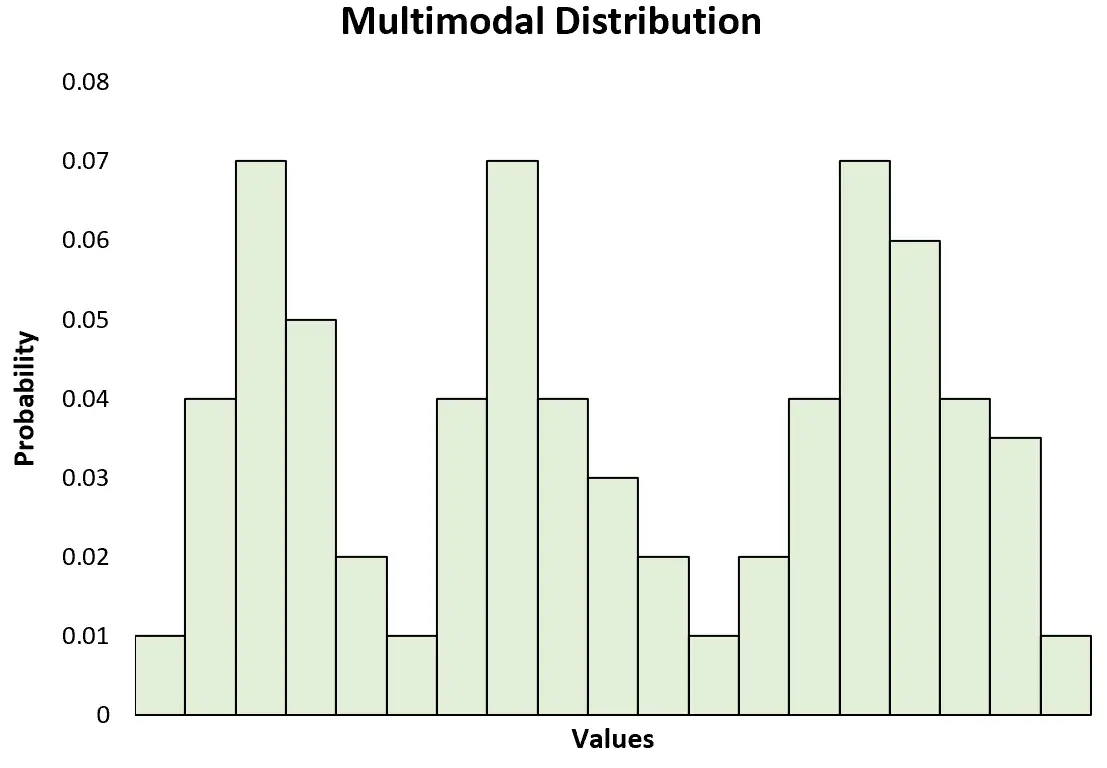
Примітка. Бімодальний розподіл — це лише певний тип мультимодального розподілу.

Приклади унімодальних розподілів

Ось кілька прикладів унімодальних розподілів на практиці.

Приклад 1: Вага немовлят при народженні

Добре відомо, що розподіл ваги новонароджених є унімодальним розподілом із середнім показником близько 7,5 фунтів. Якщо ми створимо гістограму ваги немовлят, ми побачимо «пік» у 7,5 фунтів, де одні діти важать більше, а інші менше.

Приклад 2: бали ACT

Середній бал ACT для старшокласників у Сполучених Штатах становить приблизно 21, причому одні учні мають нижчі, а інші вищі. Якщо ми створимо гістограму балів ACT для всіх студентів у Сполучених Штатах, ми побачимо єдиний «пік» у 21 рік, з вищими балами для одних студентів і нижчими для інших.

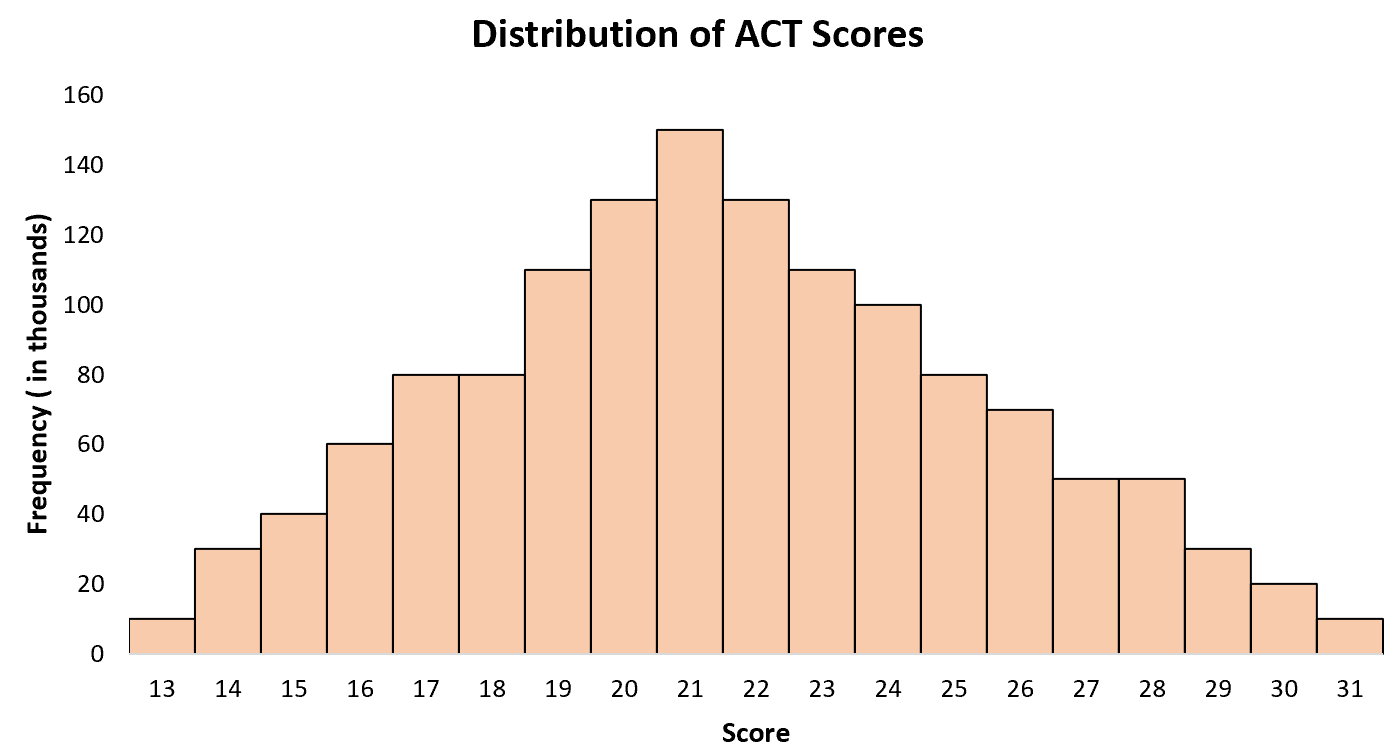
Приклад 3: розміри взуття

Розподіл розмірів чоловічого взуття є унімодальним із «піком» біля 10. Якщо ми створимо гістограму всіх розмірів чоловічого взуття, ми побачимо один пік на 10, де одні чоловіки носять більший розмір, а інші — більший. розмір. менший розмір.

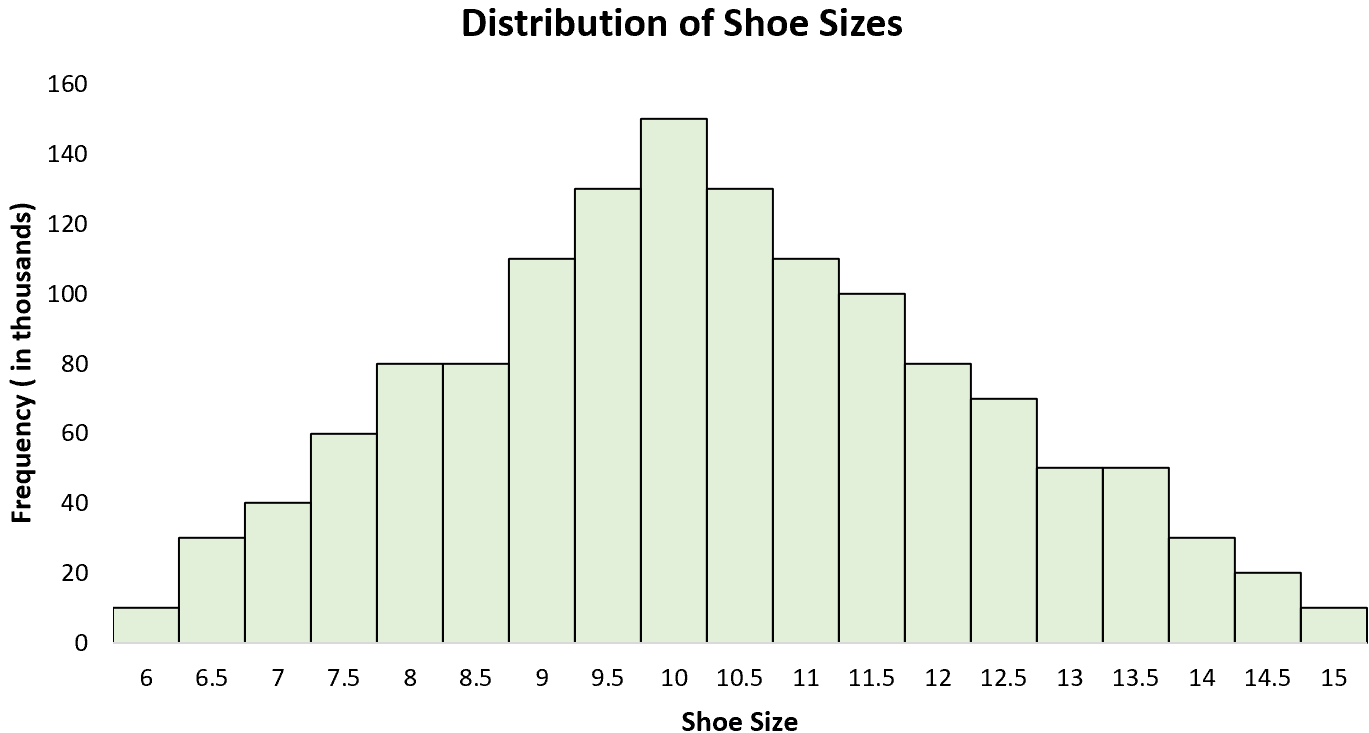
Унімодальні розподіли в статистиці

Усі наступні розподіли ймовірностей у статистиці є унімодальними розподілами:

Нормальний розподіл

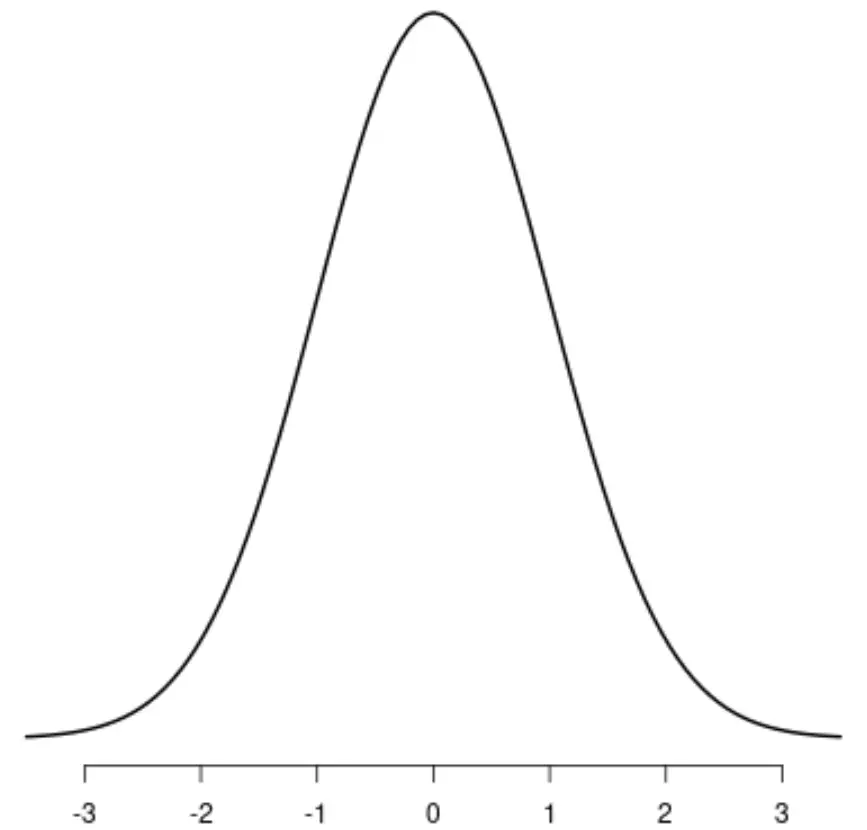
Розподіл t

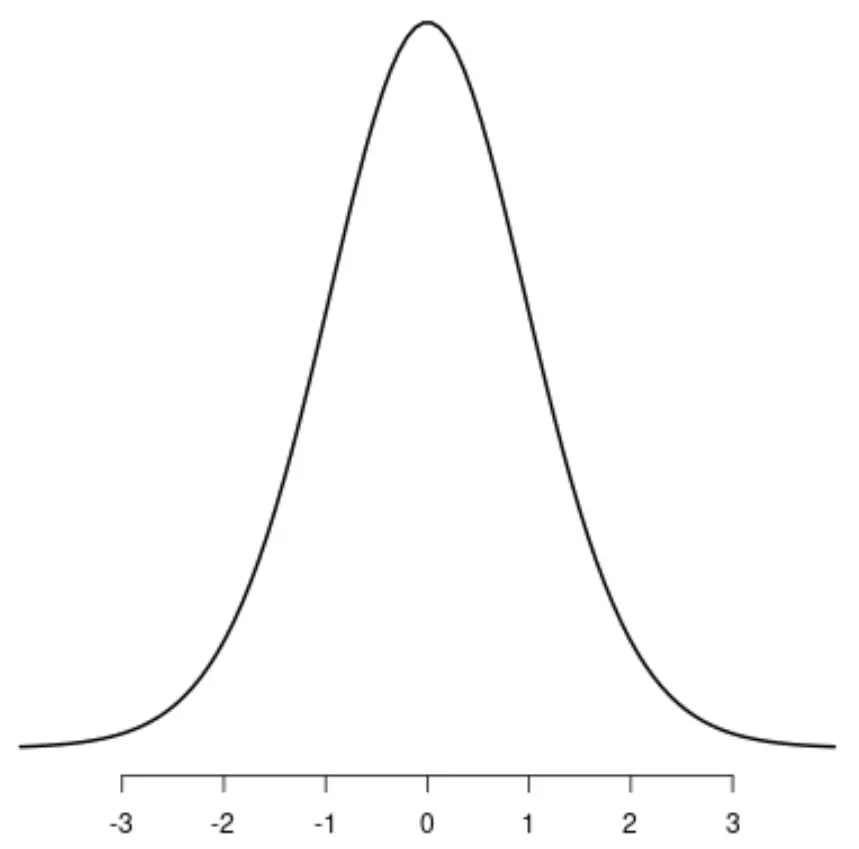
Рівномірний розподіл

Розподіл Коші

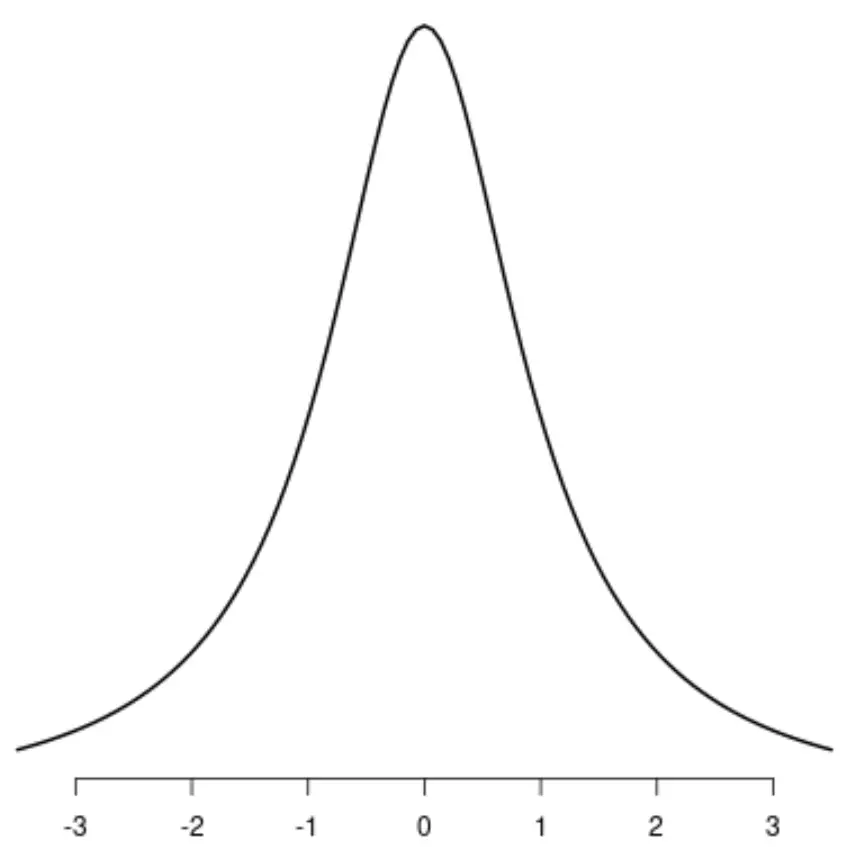
Зверніть увагу, що кожен із цих розподілів має один чіткий пік.

Як аналізувати унімодальні розподіли

Ми часто описуємо унімодальний розподіл, використовуючи три різні міри центральної тенденції :

• Середнє : середнє значення
• Медіана : середнє значення
• Режим : значення, яке з’являється найчастіше

Залежно від асиметрії розподілу ці три вимірювання можна знайти в різних місцях.

Лівосторонній розподіл: Середнє < Медіана < Мода

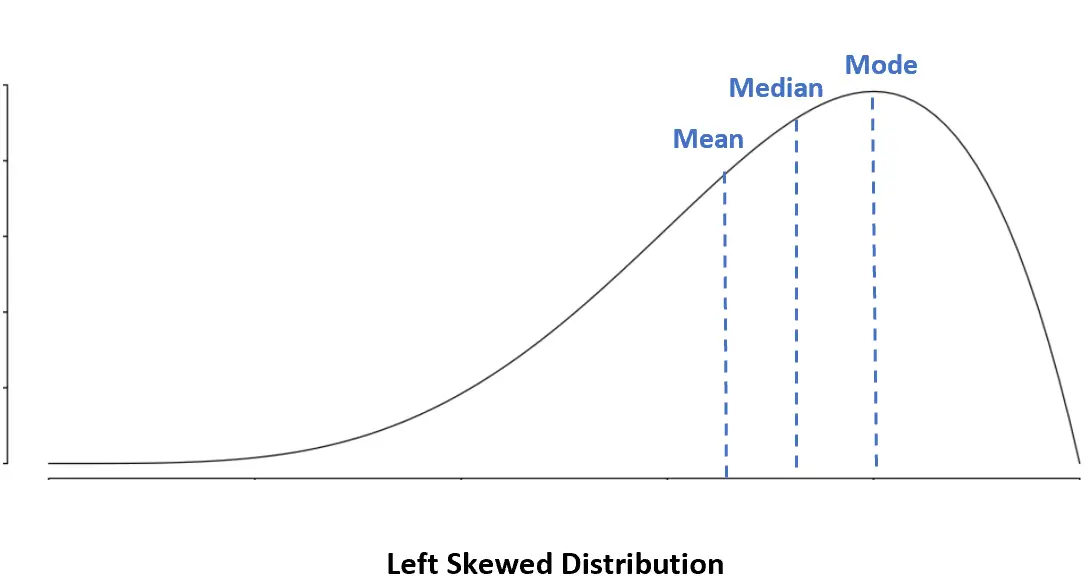
У лівосторонньому розподілі середнє значення менше медіани.

Правосторонній розподіл: режим < медіана < середнє

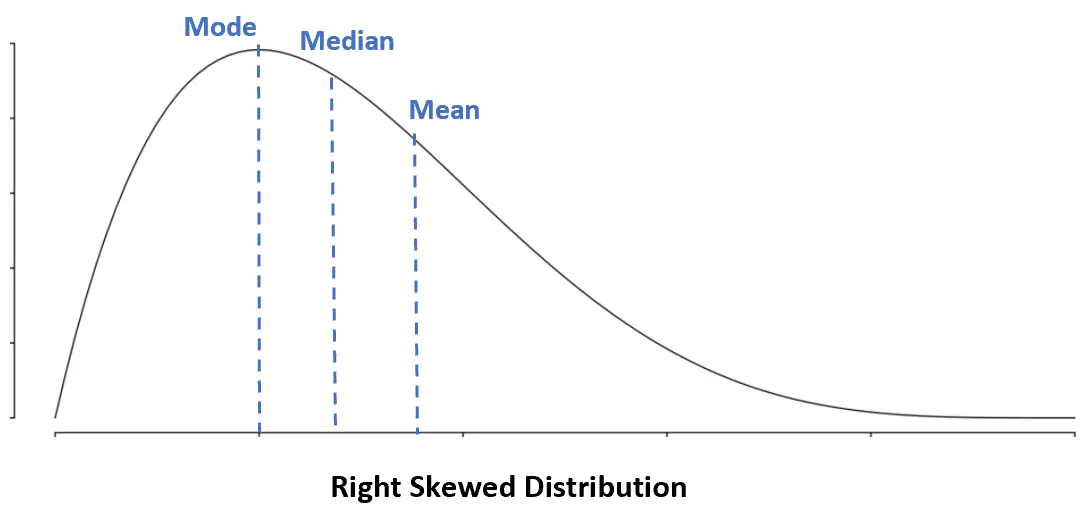
У правосторонньому розподілі середнє більше, ніж медіана.

Без зміщення: середнє = медіана = режим

У симетричному розподілі середнє, медіана та мода рівні.

Додаткові ресурси

Лівий або правий перекіс розподілу
Симетричні розподіли: визначення + приклади