Що таке факторний дисперсійний аналіз? (визначення & #038; приклад)

Факторний дисперсійний аналіз — це будь-який дисперсійний аналіз («дисперсійний аналіз»), який використовує два або більше незалежних факторів і одну змінну відповіді.

Цей тип дисперсійного аналізу слід використовувати щоразу, коли ви хочете зрозуміти, як два або більше факторів впливають на змінну відповіді та чи існує вплив взаємодії між факторами на змінну відповіді.

У цьому підручнику наведено кілька прикладів ситуацій, у яких можна використовувати факторний дисперсійний аналіз, а також покроковий приклад того, як виконати факторний дисперсійний аналіз.

Примітка. Двосторонній дисперсійний аналіз є типом факторного дисперсійного аналізу.

Приклади використання факторного дисперсійного аналізу

Факторний дисперсійний аналіз можна використовувати в кожній із наведених нижче ситуацій.

Приклад 1: Вирощування рослин

Ботанік хоче зрозуміти, як сонце та частота поливу впливають на ріст рослин. Вона висаджує 100 насінин і дає їм рости протягом трьох місяців у різних умовах сонячного освітлення та частоти поливу. Через три місяці вона записує висоту кожної рослини.

У цьому випадку він має такі змінні:

• Змінна відповіді: ріст рослини
• Фактори: сонячне світло, частота поливу

І вона хоче відповісти на такі запитання:

• Чи впливає сонце на ріст рослин?
• Чи впливає частота поливу на ріст рослин?
• Чи існує взаємодія між перебуванням на сонці та частотою поливу?

Вона може використовувати факторний дисперсійний аналіз для цього аналізу, оскільки хоче зрозуміти, як два фактори впливають на одну змінну відповіді.

Приклад 2: Результати іспиту

Професор хоче зрозуміти, як час занять і метод навчання впливають на результати іспиту. Він використовує два різні методи навчання та два різні години навчання (рано вранці та рано вдень) і записує середні бали кожного студента за іспит наприкінці семестру.

У цьому випадку він має такі змінні:

• Змінна відповіді: іспитовий бал
• Фактори: метод навчання, час навчання

І він хотів би відповісти на такі запитання:

• Чи впливає метод навчання на результати іспиту?
• Чи впливає час навчання на результати іспиту?
• Чи існує ефект взаємодії між методом навчання та часом навчання?

Для цього аналізу він може використовувати факторний дисперсійний аналіз, оскільки хоче зрозуміти, як два фактори впливають на одну змінну відповіді.

Приклад 3: Річний дохід

Економіст збирає дані, щоб зрозуміти, як рівень освіти (диплом про середню освіту, диплом коледжу, ступінь магістра), сімейний стан (неодружений, розлучений, одружений) і регіон (північ, схід, південь, захід) впливають на річний дохід.

У цьому випадку він має такі змінні:

• Змінна відповіді: річний дохід
• Фактори: рівень освіти, сімейний стан, регіон

І він хотів би відповісти на такі запитання:

• Чи впливає рівень освіти на дохід?
• Чи впливає сімейний стан на дохід?
• Чи впливає регіон на дохід?
• Чи існує ефект взаємодії між цими трьома незалежними факторами?

Для цього аналізу він може використовувати факторний дисперсійний аналіз, оскільки хоче зрозуміти, як три фактори впливають на одну змінну відповіді.

Покроковий приклад факторного дисперсійного аналізу

Ботанік хоче знати, чи впливає сонячне світло та частота поливу на ріст рослин. Вона висаджує 40 насінин і дає їм рости протягом двох місяців у різних умовах сонячного освітлення та частоти поливу. Через два місяці вона записує висоту кожної рослини.

Результати наведені нижче:

Ми бачимо, що в кожній комбінації умов було вирощено п’ять рослин.

Наприклад, п’ять рослин вирощували при щоденному поливі та без сонячного світла, і їхня висота через два місяці становила 4,8 дюйма, 4,4 дюйма, 3,2 дюйма, 3,9 дюйма та 4,4 дюйма:

Ботанік використовує ці дані для виконання факторного дисперсійного аналізу в Excel і отримує такий результат:

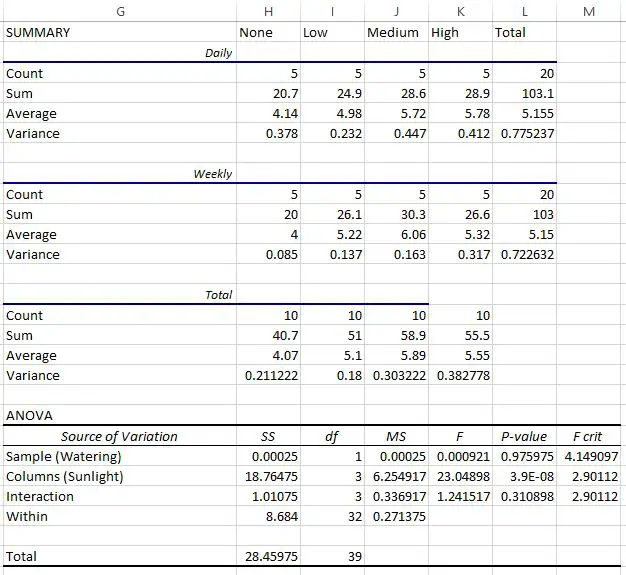
Остання таблиця показує результат факторного дисперсійного аналізу:

• P-значення для взаємодії між частотою поливу та сонячним промінням становило 0,310898 . Це не є статистично значущим на рівні 0,05 альфа.
• P-значення частоти поливу становило 0,975975 . Це не є статистично значущим на рівні 0,05 альфа.
• P-значення для перебування на сонці становило 3,9E-8 (0,000000039) . Це статистично значуще на альфа-рівні 0,05.

Ми можемо зробити висновок, що вплив сонячного світла є єдиним фактором зі статистично значущим впливом на ріст рослин.

Ми також можемо зробити висновок, що немає ніякого ефекту взаємодії між впливом сонця та частотою поливу, і що частота поливу не має статистично значущого впливу на ріст рослин. рослини.

Додаткові ресурси

У наступних посібниках надається додаткова інформація про моделі ANOVA:

Вступ до одностороннього дисперсійного аналізу
Вступ до двостороннього дисперсійного аналізу
Вступ до дисперсійного аналізу повторних вимірювань
Відмінності між ANOVA, ANCOVA, MANOVA та MANCOVA