Повний посібник: факторний дизайн 2×2

Факторний план 2 × 2 — це тип експериментального плану, який дозволяє дослідникам зрозуміти вплив двох незалежних змінних (кожна має два рівні ) на одну залежну змінну.

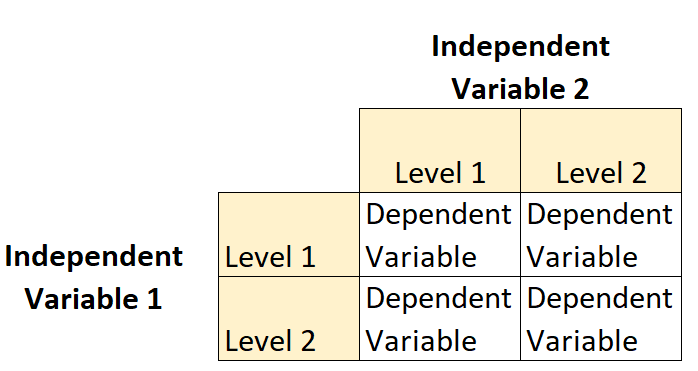
Наприклад, припустімо, що ботанік хоче зрозуміти вплив сонячного світла (низького чи сильного) і частоти поливу (щодня чи щотижня) на ріст певного виду рослин.

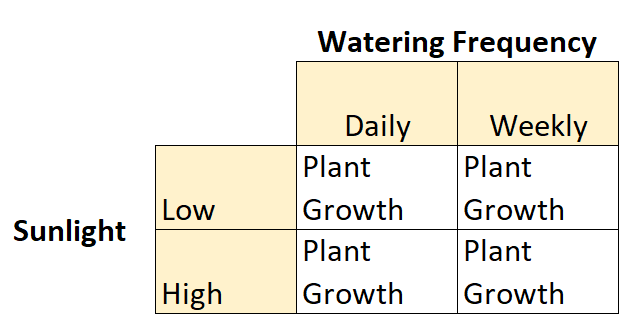
Це приклад факторного плану 2×2, оскільки є дві незалежні змінні, кожна з яких має два рівні:

• Незалежна змінна №1: сонячне світло
  • Рівні: низький, високий
• Незалежна змінна №2: частота поливу
  • Рівні: щоденний, тижневий

І є залежна змінна: ріст рослин.

Мета факторного дизайну 2 × 2

Факторний план 2×2 дає змогу аналізувати такі ефекти:

Основні ефекти: це вплив окремої незалежної змінної на залежну змінну.

Наприклад, у нашому попередньому сценарії ми могли б проаналізувати такі основні ефекти:

• Основний вплив сонячного світла на ріст рослин.
  • Ми можемо знайти середній ріст усіх рослин, які отримували слабке сонячне світло.
  • Ми можемо знайти середній ріст усіх рослин, які отримали сильне сонячне світло.
• Основний вплив частоти поливу на ріст рослин.
  • Ми можемо знайти середній ріст усіх рослин, які поливають щодня.
  • Ми можемо знайти середній ріст усіх рослин, які поливали щотижня.

Ефекти взаємодії: вони виникають, коли вплив однієї незалежної змінної на залежну змінну залежить від рівня іншої незалежної змінної.

Наприклад, у нашому попередньому сценарії ми могли б проаналізувати такі ефекти взаємодії:

• Чи залежить вплив сонячного світла на ріст рослин від частоти поливу?
• Чи залежить вплив частоти поливу на ріст рослин від сонячного світла?

Візуалізуйте основні ефекти та ефекти взаємодії

Коли ми використовуємо факторний план 2 × 2, ми часто малюємо середні на графіку, щоб краще зрозуміти вплив незалежних змінних на залежну змінну.

Для прикладу розглянемо такий сюжет:

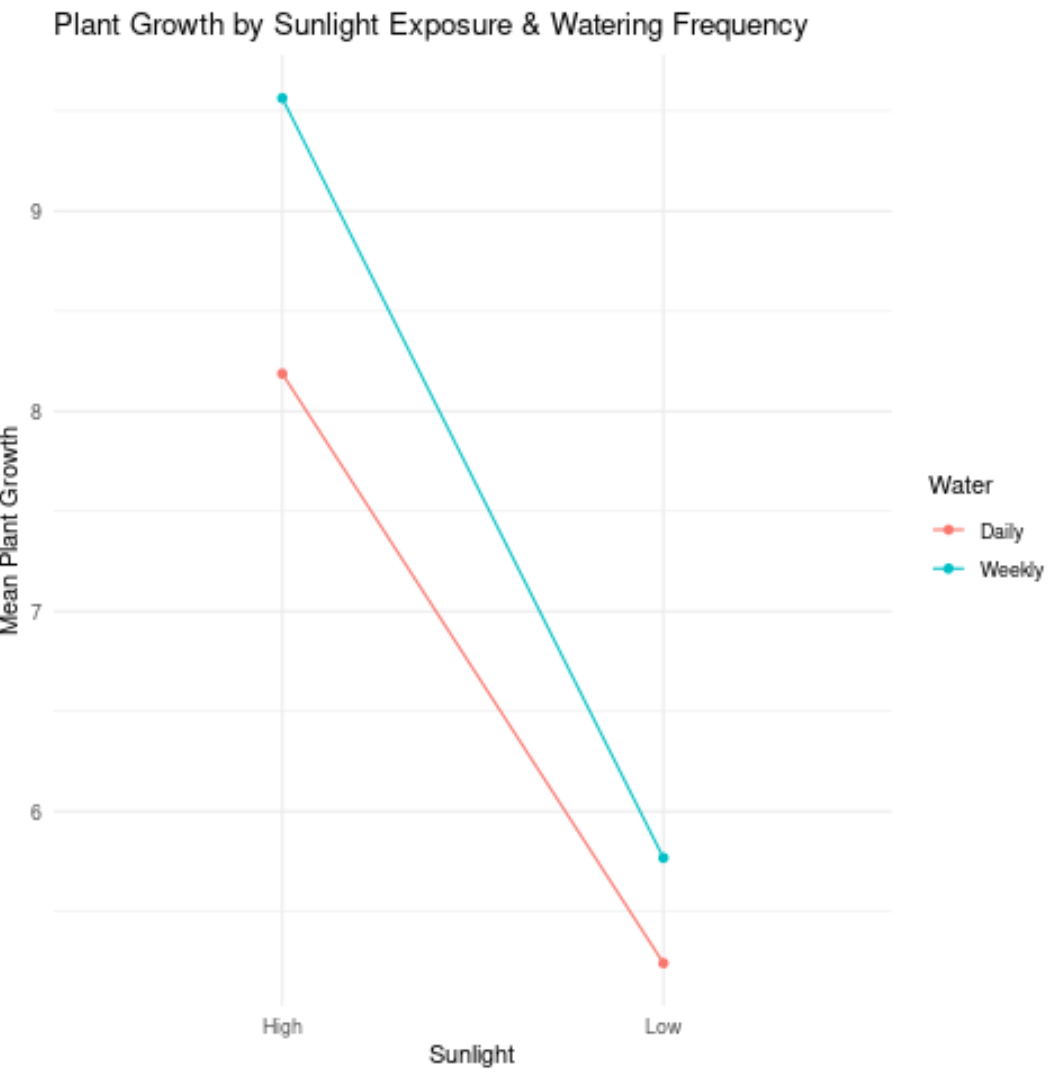
Ось як інтерпретувати значення на графіку:

• Середній ріст рослин, які отримували інтенсивне сонячне світло та щоденний полив, становив приблизно 8,2 дюйма.
• Середній ріст рослин, які отримували високе сонячне світло та щотижневий полив, становив приблизно 9,6 дюйма.
• Середній ріст рослин, які отримували слабке сонце та щоденний полив, становив приблизно 5,3 дюйма.
• Середній ріст рослин, які отримували слабке сонце та щотижневий полив, становив приблизно 5,8 дюйма.

Щоб визначити, чи існує ефект взаємодії між двома незалежними змінними, просто перевірте, паралельні лінії чи ні:

• Якщо дві лінії графіка паралельні, ефекту взаємодії немає.
• Якщо дві лінії графіка не паралельні, виникає ефект взаємодії.

На попередньому графіку дві лінії були приблизно паралельні, тому, ймовірно, немає ефекту взаємодії між частотою поливу та перебуванням на сонці.

Однак розглянемо наступний сюжет:

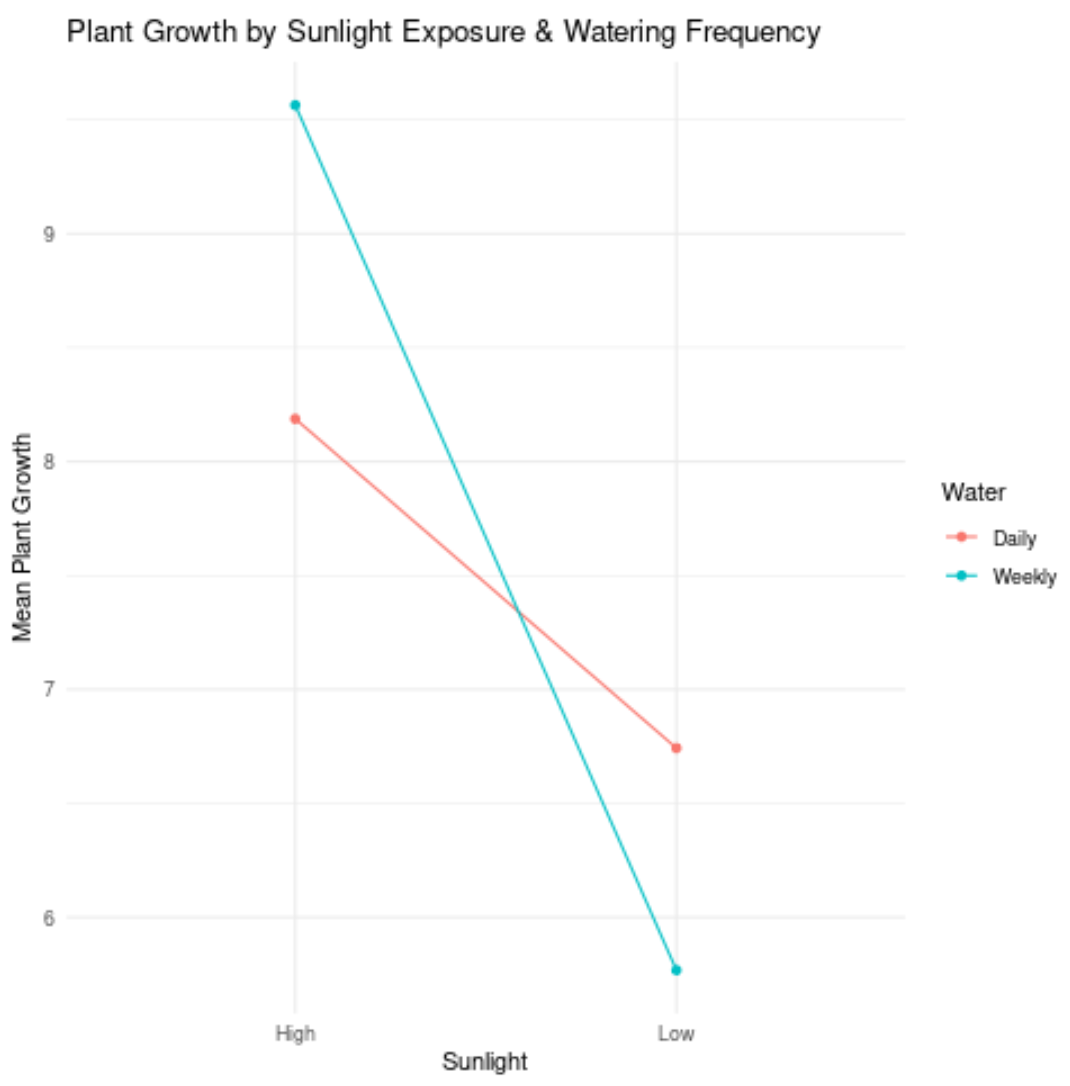
Ці дві лінії зовсім не паралельні (насправді вони перетинаються!), що вказує на те, що між ними, ймовірно, існує ефект взаємодії.

Наприклад, це означає, що вплив сонячного світла на ріст рослин залежить від частоти поливу.

Іншими словами, сонячне світло та частота поливу незалежно не впливають на ріст рослин. Скоріше існує ефект взаємодії між двома незалежними змінними.

Як аналізувати факторний план 2×2

Побудова середніх значень — це візуальний спосіб перевірити вплив незалежних змінних на залежну змінну.

Однак ми також можемо виконати двосторонній дисперсійний аналіз , щоб формально перевірити, чи мають незалежні змінні статистично значущий зв’язок із залежною змінною.

Наприклад, наступний код показує, як виконати двосторонній дисперсійний аналіз для нашого гіпотетичного заводського сценарію в R:

 #make this example reproducible
set. seeds (0)

df <- data. frame (sunlight = rep(c(' Low ', ' High '), each = 30 ),
                 water = rep(c(' Daily ', ' Weekly '), each = 15 , times = 2 ),
                 growth = c(rnorm(15, 6, 2), rnorm(15, 7, 3), rnorm(15, 7, 2),
                                   rnorm(15, 10, 3)))

#fit the two-way ANOVA model
model <- aov(growth ~ sunlight * water, data = df)

#view the model output
summary(model)

               Df Sum Sq Mean Sq F value Pr(>F)   
sunlight 1 52.5 52.48 8.440 0.00525 **
water 1 31.6 31.59 5.081 0.02813 * 
sunlight:water 1 12.8 12.85 2.066 0.15620   
Residuals 56 348.2 6.22                   
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Ось як інтерпретувати результат ANOVA:

• P-значення, пов’язане з сонячним світлом, становить 0,005 . Оскільки це число менше 0,05, це означає, що вплив сонячного світла має статистично значущий вплив на ріст рослин.
• P-значення, пов’язане з водою, становить 0,028 . Оскільки цей показник менше 0,05, це означає, що частота поливу також має статистично значущий вплив на ріст рослин.
• Р-значення взаємодії сонячного світла і води становить 0,156 . Оскільки цей показник не менше 0,05, це означає відсутність ефекту взаємодії між сонячним світлом і водою.

Додаткові ресурси

Повний посібник: факторний дизайн 2 × 3
Що таке рівні незалежної змінної?
Незалежні або залежні змінні
Що таке факторний дисперсійний аналіз?