Функція густини

за Редакція 5 Серпня, 2023 Ймовірність 0 коментарів

У цій статті ви дізнаєтесь, що таке функція щільності, як обчислюється ймовірність на основі функції щільності та характеристики цієї імовірнісної функції. Крім того, ви зможете побачити відмінності між функцією щільності та функцією розподілу.

Що таке функція густини?

Функція щільності , також звана функцією щільності ймовірності , є математичною функцією, яка описує ймовірність того, що безперервна випадкова змінна набуває певного значення.

Іншими словами, функція щільності, пов’язана зі змінною, математично визначає ймовірність того, що змінна приймає значення.

Наприклад, припустимо, що ймовірність того, що доросла людина має зріст понад 1,80 м у популяції, становить 35%, тоді функція щільності вказуватиме ймовірність 35% під час обчислення зазначеної ймовірності.

Іноді функцію щільності ймовірності скорочено називають PDF.

Обчисліть ймовірність за допомогою функції щільності

Щоб знайти ймовірність того, що безперервна змінна приймає значення в інтервалі, необхідно обчислити інтеграл функції щільності, пов’язаної з цією змінною між межами інтервалу.

$\displaystyle P[a\leq X\leq b]=\int_a^b f(x)dx$

золото

$f(x)$

є функцією щільності безперервної випадкової величини.

Або іншими словами, ймовірність того, що змінна набере значення в інтервалі, еквівалентна площі під функцією щільності в цьому інтервалі.

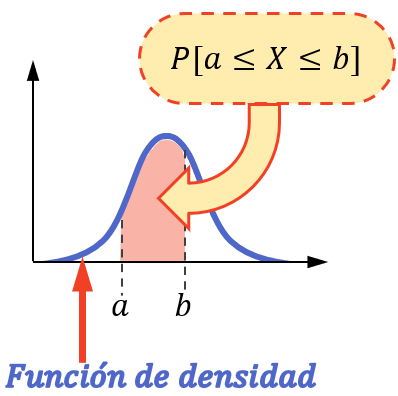
Зауважте, що обчислення ймовірності можна виконати таким чином, лише якщо статистична змінна має неперервний розподіл, наприклад нормальний розподіл, експоненціальний розподіл, розподіл Пуассона тощо.

Властивості функції густини

Функція густини має такі властивості:

Значення функції густини дорівнює нулю або додатне для будь-якого значення x.

$f(x)\geq 0$

Крім того, максимальне значення функції щільності дорівнює 1.

$f(x)\leq 1$

Насправді загальна площа під графіком функції щільності завжди еквівалентна 1, незалежно від змінної, оскільки вона відповідає набору всіх ймовірностей.

$\displaystyle \int_{-\infty}^{+\infty} f(x)dx=1$

Як пояснювалося в попередньому розділі, ймовірність того, що безперервна змінна приймає значення в інтервалі, обчислюється за допомогою інтеграла функції щільності в цьому інтервалі.

$\displaystyle P[a\leq X\leq b]=\int_a^b f(x)dx=F(b)-F(a)$

Функція густини та функція розподілу

У цьому останньому розділі ми побачимо, чим відрізняються функція щільності та функція розподілу, оскільки це два типи імовірнісних функцій, які зазвичай плутають.

Математично функція розподілу еквівалентна інтегралу функції щільності , тому функція розподілу описує кумулятивну ймовірність безперервної змінної.

Тобто образ функції розподілу для будь-якого значення дорівнює ймовірності того, що змінна приймає це значення або нижче значення.

Отже, математичний зв’язок між цими двома типами функцій такий:

$\displaystyle P[X\leq a]=\int_{-\infty}^a f(x)dx=F(a)$

золото

$f(x)$

є функцією густини і

$F(x)$

є функцією розподілу.

Зверніть увагу на те, як змінюється графічне представлення функції щільності відносно її функції розподілу змінної, яка відповідає нормальному розподілу із середнім значенням 1 і стандартним відхиленням 0,5:

різниця між функцією розподілу та функцією густини

Щоб дізнатися більше про функцію розповсюдження, натисніть посилання нижче:

➤ Див.: функція розподілу

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше