Чому розмір вибірки важливий? (пояснення та приклади)
Розмір вибірки означає загальну кількість людей, залучених до експерименту чи дослідження.
Розмір вибірки важливий, оскільки він безпосередньо впливає на точність, з якою ми можемо оцінити параметри сукупності.
Щоб зрозуміти, чому це так, допоможе базове розуміння довірчих інтервалів.
Коротке пояснення довірчих інтервалів
У статистиці ми часто прагнемо виміряти параметри сукупності – числа, які описують певні характеристики цілої сукупності.
Наприклад, нам може бути цікаво виміряти середній зріст усіх людей у певному місті.
Однак часто збір даних про кожну особину в популяції є занадто дорогим і трудомістким. Тому ми зазвичай беремо випадкову вибірку з сукупності та використовуємо дані вибірки для оцінки параметра сукупності.
Наприклад, ми могли б зібрати дані про зріст 100 випадкових людей у місті. Потім ми можемо обчислити середній розмір особин у вибірці. Однак ми не можемо бути впевнені, що вибіркове середнє точно відповідає середньому по сукупності.
Щоб врахувати цю невизначеність, ми можемо створити довірчий інтервал . Довірчий інтервал – це діапазон значень, який, ймовірно, містить параметр сукупності з певним рівнем довіри.
Формула для розрахунку довірчого інтервалу для середнього сукупності:
Довірчий інтервал = x +/- z*(s/√ n )
золото:
- x : вибіркове середнє
- z: вибране значення z
- s: вибіркове стандартне відхилення
- n: розмір вибірки
Значення z, яке ви використовуєте, залежить від вибраного рівня достовірності. У наведеній нижче таблиці показано значення z, яке відповідає найпоширенішим виборам рівня достовірності:
| Рівень впевненості | значення z |
|---|---|
| 0,90 | 1645 |
| 0,95 | 1,96 |
| 0,99 | 2.58 |
Зв’язок між розміром вибірки та довірчими інтервалами
Припустімо, ми хочемо оцінити середню вагу популяції черепах. Ми збираємо випадкову вибірку черепах із такою інформацією:
- Обсяг вибірки n = 25
- Середня маса зразка х = 300
- Стандартне відхилення вибірки s = 18,5
Ось як розрахувати 90% довірчий інтервал для справжньої середньої ваги сукупності:
90% довірчий інтервал: 300 +/- 1,645*(18,5/√ 25 ) = [293,91, 306,09]
Ми на 90% впевнені, що фактична середня вага черепах у популяції становить від 293,91 до 306,09 фунтів.
Тепер припустімо, що замість 25 черепах ми збираємо дані про 50 черепах.
Ось як розрахувати 90% довірчий інтервал для справжньої середньої ваги сукупності:
90% довірчий інтервал: 300 +/- 1,645*(18,5/√ 50 ) = [295,79, 304,30]
Зауважте, що цей довірчий інтервал вужчий за попередній. Це означає, що наша оцінка справжньої середньої ваги популяції черепах більш точна.
А тепер припустімо, що ми збираємо дані про 100 черепах.
Ось як розрахувати 90% довірчий інтервал для справжньої середньої ваги сукупності:
90% довірчий інтервал: 300 +/- 1,645*(18,5/√ 100 ) = [296,96, 303,04]
Зауважте, що цей довірчий інтервал навіть вужчий, ніж попередній.
У наведеній нижче таблиці підсумовано кожну ширину довірчого інтервалу:
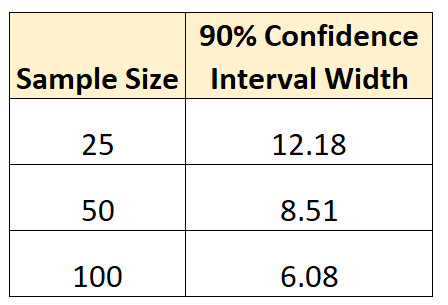
Ось підсумок: що більший розмір вибірки, то точніше ми можемо оцінити параметр сукупності .
Додаткові ресурси
Наступні навчальні посібники надають більш корисні пояснення довірчих інтервалів і розміру вибірки.
Вступ до довірчих інтервалів
4 приклади довірчих інтервалів у реальному житті
Населення проти зразок: яка різниця?