Як обчислити sxx у статистиці (з прикладом)

У статистиці Sxx являє собою суму квадратів відхилень від середнього значення x.

Це значення часто обчислюється під час підгонки простої моделі лінійної регресії вручну.

Ми використовуємо таку формулу для обчислення Sxx:

Sxx = Σ(x _i – x ) ²

золото:

• Σ : символ, що означає «сума»
• x _i : ^i-те значення x
• x : середнє значення x

У наступному прикладі показано, як використовувати цю формулу на практиці.

Приклад: обчисліть Sxx вручну

Припустімо, ми хочемо підібрати просту модель лінійної регресії до наступного набору даних:

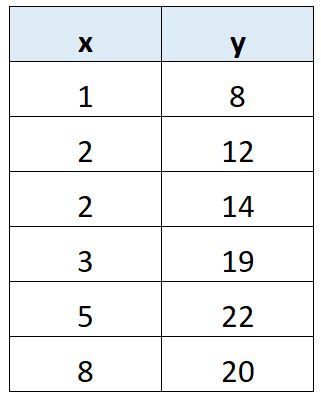
Припустімо, ми хочемо обчислити Sxx, яке представляє суму квадратів відхилень від середнього значення x.

Перш за все, ми повинні обчислити середнє значення x:

• x = (1 + 2 + 2 + 3 + 5 + 8) / 6 = 3,5

Тоді ми можемо використати таку формулу для обчислення значення Sxx:

• Sxx = Σ(x _i – x ) ²
• Sxx = (1-3,5) ² +(2-3,5) ² +(2-3,5) ² +(3-3,5) ² +(5-3,5) ² +(8- 3,5) ²
• Sxx = 6,25 + 2,25 + 2,25 + 0,25 + 2,25 + 20,25
• Sxx = 33,5

Значення Sxx виявляється рівним 33,5 .

Це говорить нам про те, що сума квадратів відхилень між окремими значеннями x і середнім значенням x дорівнює 33,5.

Зверніть увагу, що ми також можемо використовувати калькулятор Sxx для автоматичного розрахунку значення Sxx для цієї моделі:

Калькулятор повертає значення 33,5 , яке ми обчислили вручну.

Зауважте, що ми використовуємо такі формули, щоб вручну виконати просту лінійну регресію:

y = a + bx

золото:

• a = y – bx
• b = Sxy / Sxx

Розрахунок для Sxx — це просто обчислення, яке нам потрібно виконати, щоб відповідати простій моделі лінійної регресії.

Пов’язане:Як обчислити Sxy у статистиці

Додаткові ресурси

У наступних посібниках пояснюється, як виконувати інші типові завдання зі статистики:

Як виконати просту лінійну регресію вручну
Як виконати множинну лінійну регресію вручну