Як інтерпретувати співвідношення шансів
У статистиці ймовірність означає ймовірність того, що подія відбудеться. Він розраховується таким чином:
ЙМОВІРНІСТЬ:
P(подія) = (# бажаних результатів) / (# можливих результатів)
Наприклад, припустимо, що у мішку є чотири червоні кулі та одна зелена. Якщо ви закриєте очі і навмання виберіть кульку, ймовірність того, що ви виберете зелену кульку, обчислюється наступним чином:
P(зелений) = 1/5 = 0,2 .
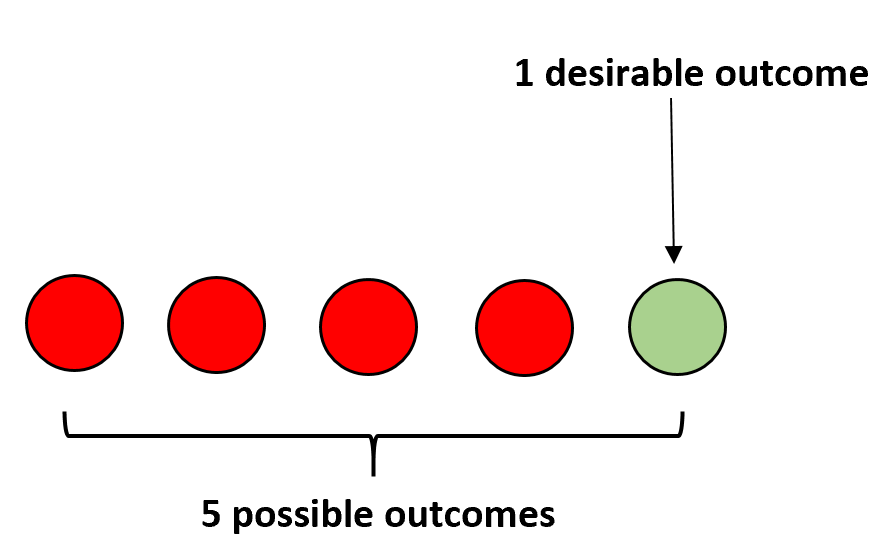
Імовірність події можна розрахувати наступним чином:
СТАВКИ:
Шанси (подія) = P (подія відбулася) / 1-P (подія відбулася)
Наприклад, шанси кинути зелену кулю становлять (0,2)/1-(0,2) = 0,2/0,8 = 0,25 .
Відношення шансів – це відношення двох ймовірностей.
ЗВІТ ПРО УДАЧУ:
Співвідношення шансів = шанси події A / шанси події B
Наприклад, ми могли б обчислити співвідношення шансів між вибором червоної та зеленої кульок.
Імовірність витягнути червону кульку становить 4/5 = 0,8 .
Шанси витягнути червону кульку становлять (0,8) / 1-(0,8) = 0,8 / 0,2 = 4 .
Співвідношення шансів на вибір червоної кулі замість зеленої розраховується таким чином:
Шанси (червоний) / Шанси (зелений) = 4 / 0,25 = 16 .
Таким чином, шанси кинути червону кулю в 16 разів більші, ніж шанси кинути зелену кулю.
Коли коефіцієнти шансів використовуються в реальному світі?
У реальному світі коефіцієнти шансів використовуються в різних контекстах, у яких дослідники хочуть порівняти шанси двох подій. Ось кілька прикладів.
Приклад №1: Інтерпретація коефіцієнтів шансів
Дослідники хочуть знати, чи нове лікування покращує шанси пацієнта отримати позитивний результат для здоров’я порівняно з існуючим лікуванням. У наведеній нижче таблиці показано кількість пацієнтів, у яких спостерігався позитивний чи негативний результат для здоров’я залежно від лікування.

Шанси пацієнта отримати позитивний результат при новому лікуванні можна розрахувати таким чином:
Шанси = P(позитивний) / 1 – P(позитивний) = (50/90) / 1-(50/90) = (50/90) / (40/90) = 1,25
Шанси пацієнта отримати позитивний результат при існуючому лікуванні можна розрахувати таким чином:
Шанси = P (позитивний) / 1 – P (позитивний) = (42/90) / 1-(42/90) = (42/90) / (48/90) = 0,875
Таким чином, співвідношення шансів на досягнення позитивного результату за допомогою нового лікування порівняно з існуючим лікуванням можна розрахувати наступним чином:
Коефіцієнт шансів = 1,25 / 0,875 = 1,428 .
Ми інтерпретуємо це так, що шанси пацієнта отримати позитивний результат при використанні нового лікування в 1,428 рази перевищують шанси пацієнта отримати позитивний результат при використанні існуючого лікування.
Іншими словами, шанси відчути позитивний результат з новим лікуванням збільшуються на 42,8% .
Приклад №2: Інтерпретація коефіцієнтів шансів
Маркетологи хочуть знати, чи реклама змушує клієнтів купувати певний товар частіше, ніж інша реклама. Тому вони показують кожну рекламу 100 людям. У наведеній нижче таблиці показано кількість людей, які придбали товар, залежно від оголошення, яке вони побачили:
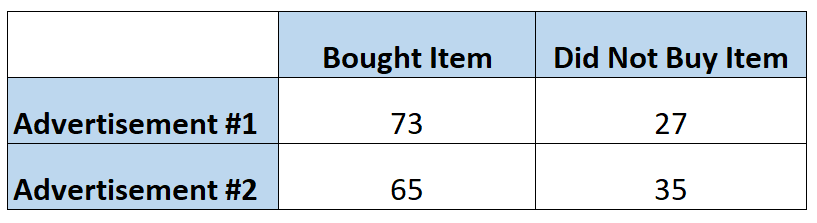
Імовірність того, що особа придбає товар після перегляду першої реклами, можна розрахувати таким чином:
Шанси = P(куплений) / 1 – P(куплений) = (73/100) / 1-(73/100) = (73/100) / (27/100) = 2,704
Шанси того, що особа придбає товар після перегляду другої реклами, можна розрахувати таким чином:
Шанси = P(куплений) / 1 – P(куплений) = (65/100) / 1-(65/10) = (65/100) / (35/100) = 1,857
Таким чином, співвідношення шансів для того, хто купує товар після перегляду першої реклами, і купівлі після перегляду другої реклами можна розрахувати таким чином:
Коефіцієнт шансів = 2,704 / 1,857 = 1,456 .
Ми інтерпретуємо це так, що ймовірність того, що особа придбає товар після перегляду першої реклами, у 1,456 рази перевищує ймовірність того , що особа придбає товар після перегляду другої реклами.
Іншими словами, шанси придбати товар збільшуються на 45,6% завдяки першому розміщенню.
Додаткові ресурси
Як розрахувати співвідношення шансів і відносний ризик у Excel
Як інтерпретувати співвідношення шансів менше 1
Як інтерпретувати відносний ризик