Накопичена абсолютна частота

У цій статті пояснюється, що таке накопичена абсолютна частота та для чого вона використовується. Отже, ви знайдете визначення кумулятивної абсолютної частоти, як отримати кумулятивну абсолютну частоту з набору даних і, крім того, дві вправи, розв’язані крок за кроком.

Що таке кумулятивна абсолютна частота?

У статистиці кумулятивна абсолютна частота — це кумулятивна сума абсолютних частот. Тобто кумулятивна абсолютна частота значення дорівнює абсолютній частоті цього значення плюс абсолютні частоти всіх значень, менших за нього.

Зазвичай у статистиці велика літера F з нижнім індексом i використовується для представлення сукупної абсолютної частоти значення i , тому символом для сукупної абсолютної частоти є F _i .

Логічно, щоб зрозуміти, що означає накопичена абсолютна частота, вам потрібно чітко знати концепцію абсолютної частоти, тому рекомендується ознайомитися з наступною статтею, перш ніж продовжити пояснення.

Як розрахувати кумулятивну абсолютну частоту

Кроки для обчислення сукупної абсолютної частоти такі:

1. Створіть таблицю з усіма різними значеннями, які з’являються в наборі даних, тобто розмістіть кожне окреме значення в рядку таблиці.
2. Визначає абсолютну частоту кожного значення.
3. Знайдіть сукупну абсолютну частоту кожного значення, яка обчислюється додаванням абсолютної частоти самого значення плюс абсолютні частоти всіх менших значень.

Майте на увазі, що якщо змінна неперервна або є багато різних значень, ви повинні спочатку згрупувати дані в інтервали, а потім застосувати описані вище дії, щоб знайти кумулятивну абсолютну частоту.

Приклади кумулятивної абсолютної частоти

Щоб ви могли побачити, як обчислюється кумулятивна абсолютна частота, нижче наведено два приклади з реального світу, крок за кроком. У першому прикладі було розраховано кумулятивні абсолютні частоти дискретної змінної, а на другому кроці – безперервної змінної.

Приклад 1: дискретна змінна

• Оцінки, отримані за статистикою в класі з 30 учнів, такі. Яка сукупна абсолютна частота кожної ноти?

Оскільки всі числа можуть бути лише цілими, це дискретна змінна. Тому немає необхідності групувати дані в інтервали.

Отже, щоб визначити кумулятивну абсолютну частоту, ми повинні спочатку знайти абсолютну частоту кожного значення, яка є кількістю разів, коли кожне значення з’являється в статистичній вибірці.

Тепер, коли ми знаємо абсолютну частоту, ми можемо обчислити сукупну абсолютну частоту. Для цього у нас є два варіанти: або ми додаємо абсолютну частоту значення плюс усі абсолютні частоти найменших значень, або, навпаки, ми додаємо абсолютну частоту значення плюс кумулятивну абсолютну частоту попередніх значень . значення.

Коротко кажучи, таблиця з абсолютною сукупною частотою вправ така:

Зауважте, що кумулятивна абсолютна частота останнього значення завжди відповідає загальній кількості даних. Інакше це означає, що ви помилилися в розрахунках.

Приклад 2: безперервна змінна

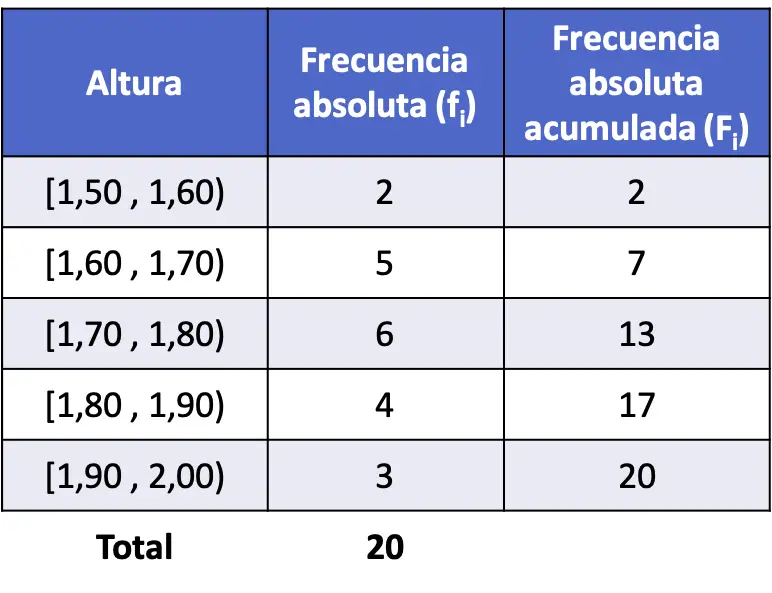
• Було виміряно зріст 20 людей і отримано результати, наведені нижче. Розділяє дані на інтервали та обчислює кумулятивну абсолютну частоту для кожного інтервалу.

Розподіл у цьому прикладі неперервний, оскільки можуть бути десяткові числа, тому найкраще згрупувати дані в різні інтервали.

Отже, ми розділяємо дані на інтервали та підраховуємо, скільки разів число з’являється в кожному інтервалі, щоб отримати абсолютну частоту:

Потім, щоб визначити кумулятивну абсолютну частоту, просто додайте абсолютні частоти всіх попередніх значень плюс абсолютну частоту відповідного значення:

Кумулятивна абсолютна частота та кумулятивна відносна частота

Різниця між кумулятивною абсолютною частотою та кумулятивною відносною частотою відповідає типу кумулятивної частоти. Накопичена абсолютна частота дорівнює сумі абсолютних частот рівних або менших значень, тоді як накопичена відносна частота еквівалентна відносним частотам рівних або менших значень.

Отже, кумулятивна абсолютна частота обчислюється з абсолютної частоти, тоді як кумулятивна відносна частота обчислюється з відносної частоти.

Ви можете побачити приклад кумулятивного розрахунку відносної частоти тут: