Як виконати аналіз основних компонентів у sas

Аналіз основних компонентів (PCA) – це техніка машинного навчання без нагляду , яка прагне знайти головні компоненти – лінійні комбінації змінних предикторів, які пояснюють значну частину варіації в наборі даних.

Найпростіший спосіб виконання PCA в SAS — використання оператора PROC PRINCOMP , який використовує такий базовий синтаксис:

 proc princomp data =my_data out =out_data outstat =stats;
    var var1 var2 var3;
run ;

Ось що робить кожна інструкція:

• дані : ім’я набору даних для використання в PCA
• out : ім’я набору даних для створення, який містить усі вихідні дані плюс оцінки головного компонента
• outstat : вказує, що має бути створений набір даних, який містить середні значення, стандартні відхилення, коефіцієнти кореляції, власні значення та власні вектори.
• var : змінні для використання для PCA з вхідного набору даних.

У наступному покроковому прикладі показано, як на практиці використовувати інструкцію PROC PRINCOMP для виконання аналізу основних компонентів у SAS.

Крок 1: Створіть набір даних

Припустимо, що ми маємо наступний набір даних, що містить різну інформацію про 20 баскетболістів:

 /*create dataset*/
data my_data;
    input points assists rebounds;
    datalines ;
22 8 4
29 7 3
10 4 12
5 5 15
35 6 2
8 3 10
10 4 8
8 4 3
2 5 17
4 5 19
9 9 4
7 6 4
31 5 3
4 6 13
5 7 8
8 8 4
10 4 8
20 4 6
25 8 8
18 8 3
;
run ;

/*view dataset*/
proc print data =my_data; 

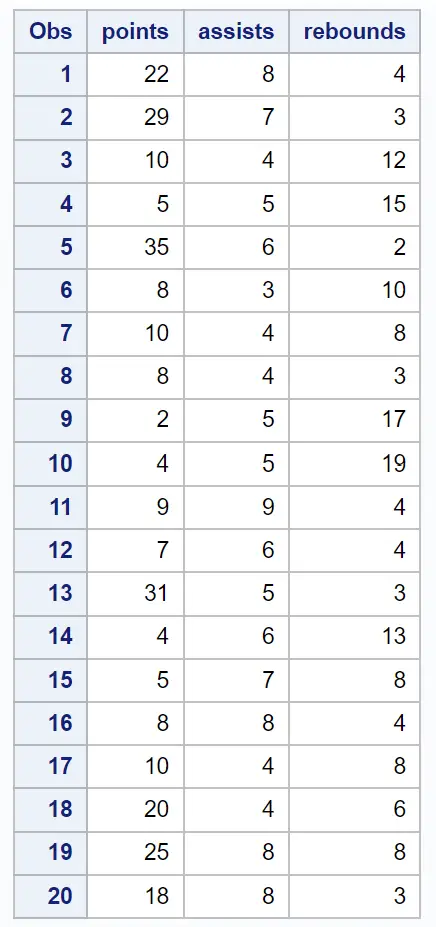
Крок 2: Виконайте аналіз головних компонентів

Ми можемо використовувати інструкцію PROC PRINCOMP для виконання аналізу головних компонентів за допомогою змінних points , assists і bounces набору даних:

 /*perform principal components analysis*/
proc princomp data =my_data out =out_data outstat =stats;
    var points assists rebounds;
run ;

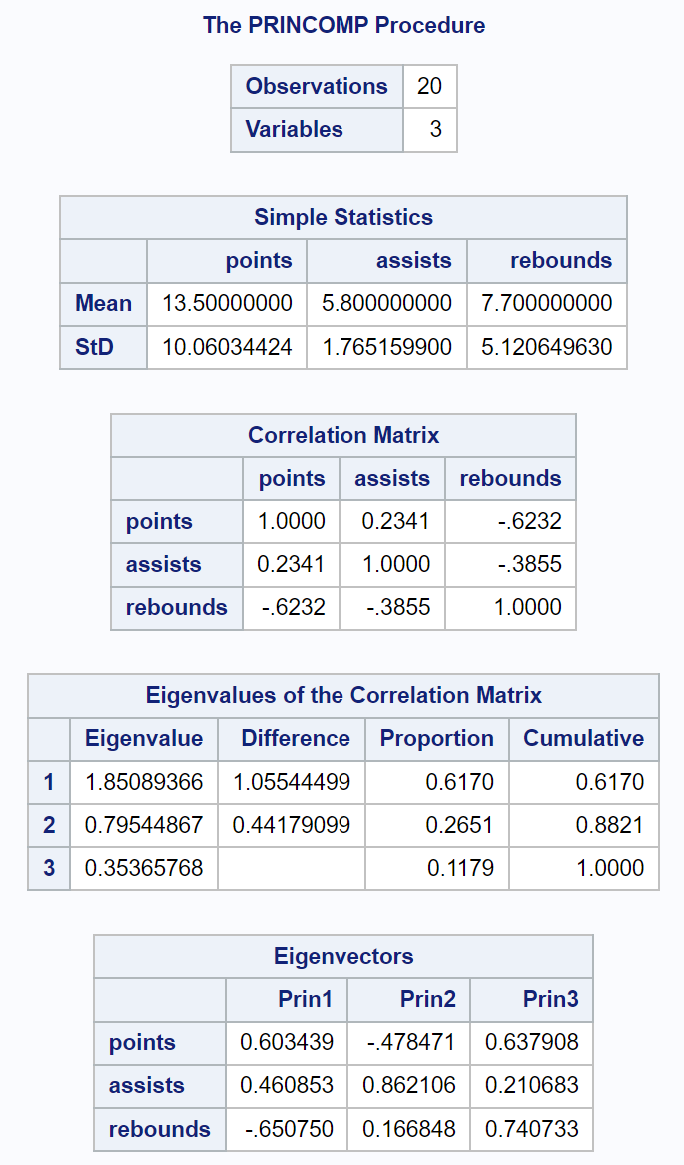
Перша частина вихідних даних відображає різні описові статистичні дані, включаючи середнє та стандартне відхилення кожної вхідної змінної, кореляційну матрицю та значення власних значень і власних векторів:

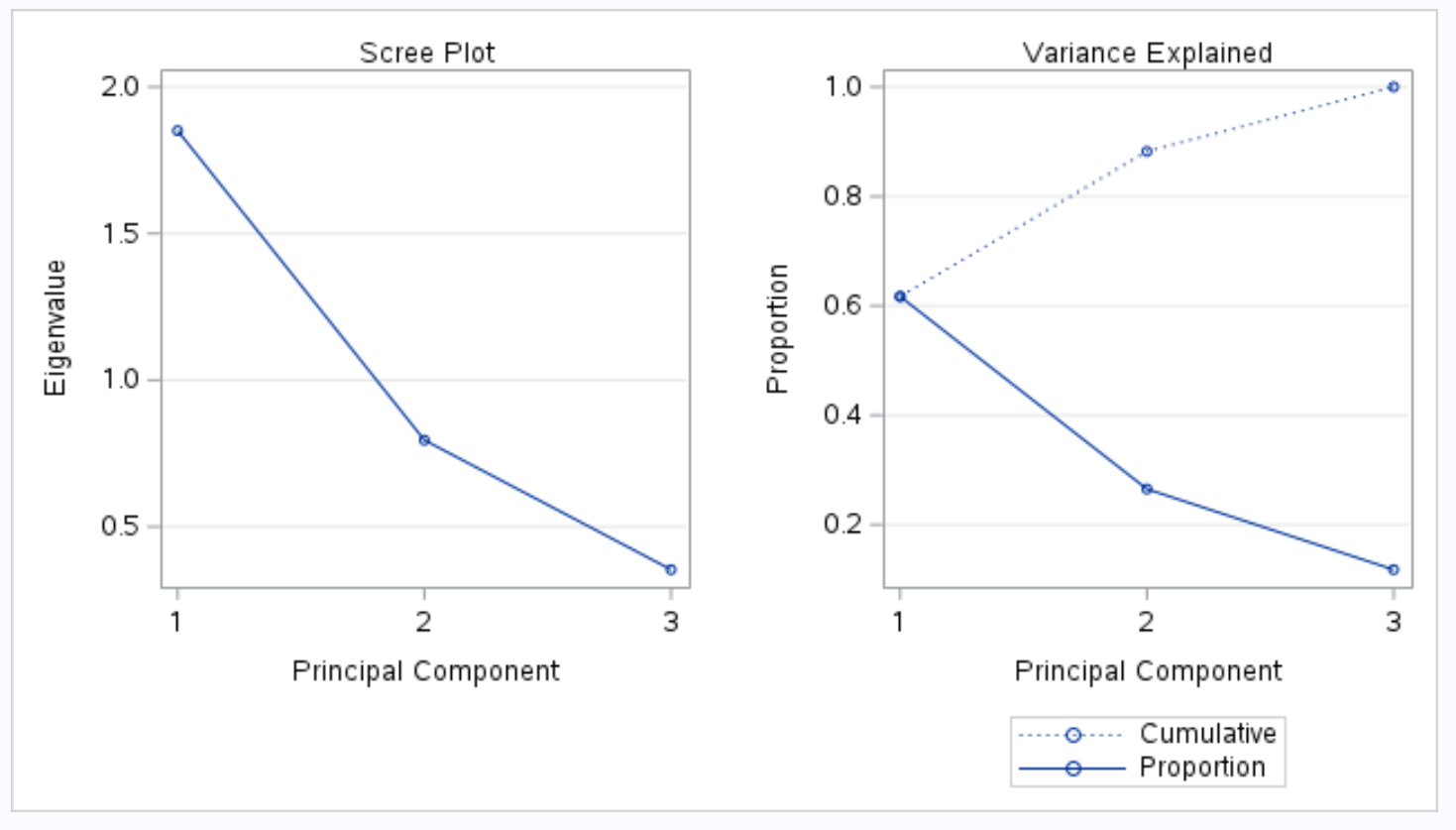
Наступна частина вихідних даних відображає графік осипів і пояснений графік дисперсії :

Коли ми виконуємо PCA, ми часто хочемо зрозуміти, який відсоток загальної варіації в наборі даних можна пояснити кожним основним компонентом.

Отримана таблиця під назвою Власні значення кореляційної матриці дозволяє нам точно побачити, який відсоток загальної варіації пояснюється кожним головним компонентом:

• Перший головний компонент пояснює 61,7% загальної варіації в наборі даних.
• Другий головний компонент пояснює 26,51% загальної варіації в наборі даних.
• Третій головний компонент пояснює 11,79% загальної варіації в наборі даних.

Зауважте, що всі відсотки в сумі становлять 100%.

Потім графік під назвою Variance Explained дозволяє візуалізувати ці значення.

На осі х відображається головний компонент, а на осі ординат – відсоток загальної дисперсії, що пояснюється кожним окремим головним компонентом.

Крок 3: Створіть біплот для візуалізації результатів

Щоб візуалізувати результати PCA для заданого набору даних, ми можемо створити біплот , який є графіком, який відображає кожне спостереження в наборі даних на площині, утвореній першими двома головними компонентами.

Ми можемо використовувати наступний синтаксис у SAS для створення біплоту:

 /*create dataset with column called obs to represent row numbers of original data*/
data biplot_data;
   set out_data;
   obs=_n_;
run ;

/*create biplot using values from first two principal components*/
proc sgplot data =biplot_data;
    scatter x =Prin1 y =Prin2 / datalabel =obs;
run ; 

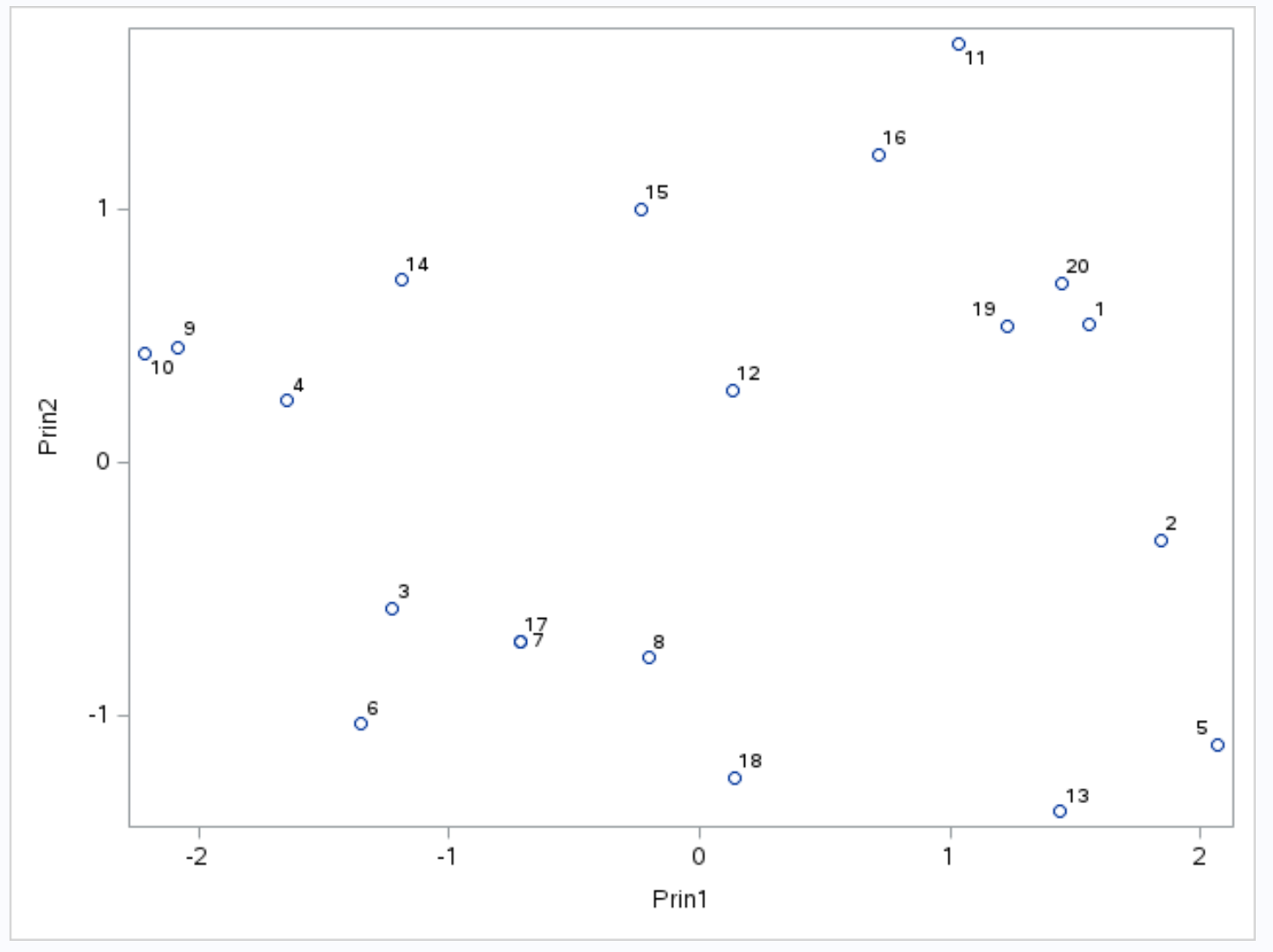
На осі X відображається перша головна компонента, на осі Y – друга головна компонента, а окремі спостереження з набору даних відображаються всередині графіка у вигляді маленьких кіл.

Спостереження, розташовані поруч на графіку, мають подібні значення для трьох змінних очок , передач і підбирань .

Наприклад, у крайньому лівому куті графіка ми бачимо, що спостереження №9 і №10 дуже близькі одне до одного.

Якщо ми звернемося до вихідного набору даних, ми побачимо такі значення для цих спостережень:

• Спостереження №9 : 2 очки, 5 передач, 17 підбирань
• Спостереження №10 : 4 очки, 5 передач, 19 підбирань

Значення подібні для кожної з трьох змінних, що пояснює, чому ці спостереження настільки близькі одне до одного на біплоті.

Ми також побачили в таблиці результатів під назвою Власні значення кореляційної матриці , що перші два основні компоненти становлять 88,21% загальної варіації в наборі даних.

Оскільки цей відсоток дуже високий, можна проаналізувати, які спостереження на біплоті близькі одне до одного, оскільки два основні компоненти, що складають біплот, складають майже всі варіації в наборі даних.

Додаткові ресурси

У наступних посібниках пояснюється, як виконувати інші типові завдання в SAS:

Як виконати просту лінійну регресію в SAS
Як виконати множинну лінійну регресію в SAS
Як виконати логістичну регресію в SAS