Що таке бальна оцінка в статистиці?
У статистиці ми часто зацікавлені у вимірюванні параметрів сукупності , тобто чисел, які описують певні характеристики цілої сукупності.
Два найпоширеніші параметри популяції:
1. Середня кількість населення: середнє значення змінної в сукупності (наприклад, середній зріст чоловіків у певному місті)
2. Частка населення: частка змінної в сукупності (наприклад, частка жителів округу, які підтримують певний закон)
Навіть якщо ми хочемо виміряти ці параметри, збирати дані про кожну людину в популяції, як правило, надто дорого та довго.
Замість цього ми беремо випадкову вибірку з сукупності та використовуємо дані вибірки для оцінки параметра сукупності.
Число, яке ми використовуємо у вибірці для оцінки параметра сукупності, називається точковою оцінкою . Це наша найкраща оцінка того, яким може бути параметр справжньої популяції.
У наступній таблиці показано точкову оцінку, яку ми використовуємо для оцінки параметрів населення:
| Міра | Параметр популяції | Бальна оцінка |
|---|---|---|
| Середній | μ (середня кількість населення) | x (вибіркове середнє) |
| Пропорція | π (частка населення) | p (пропорція зразка) |
Ми хочемо обчислити параметри сукупності, але оскільки це займає надто багато часу та коштує занадто дорого, ми замість цього використовуємо вибірки для обчислення точкових оцінок.
Наприклад, скажімо, ми хочемо оцінити середню вагу певного виду черепах у Флориді. Оскільки у Флориді є тисячі черепах, було б дуже довго і дорого обходити і зважувати кожну черепаху окремо. Замість цього ми можемо взяти просту випадкову вибірку з 50 черепах і використати середню вагу черепах у цій вибірці, щоб оцінити справжнє середнє значення популяції:

Якщо середнє значення вибірки дорівнює 150,4 фунта, то наша точкова оцінка справжньої середньої популяції всього виду буде 150,4 фунта.
Важливість репрезентативних вибірок
Коли ми збираємо вибірку з сукупності, ми в ідеалі хочемо, щоб вибірка нагадувала «міні-версію» нашої сукупності.
Вибірка вважається репрезентативною для популяції, якщо характеристики індивідів у вибірці точно відповідають характеристикам індивідів у загальній популяції.
Коли це станеться, ми можемо з упевненістю узагальнити результати вибірки на загальну сукупність і сказати, що точкова оцінка вибірки є неупередженою оцінкою справжнього параметра сукупності.
Точкові оцінки та довірчі інтервали
Хоча точкова оцінка представляє нашу найкращу можливу оцінку справжнього параметра популяції, навряд чи вона точно відповідатиме параметру популяції.
У нашому попередньому прикладі не гарантовано, що середня вага черепах у вибірці точно відповідає середній вазі черепах у всій популяції. Наприклад, ми можемо вибрати зразок, повний черепах малої ваги, або, можливо, зразок, повний важких черепах.
Отже, щоб зафіксувати цю невизначеність, ми можемо створити довірчий інтервал – діапазон значень, який, імовірно, міститиме параметр сукупності з певним рівнем довіри.
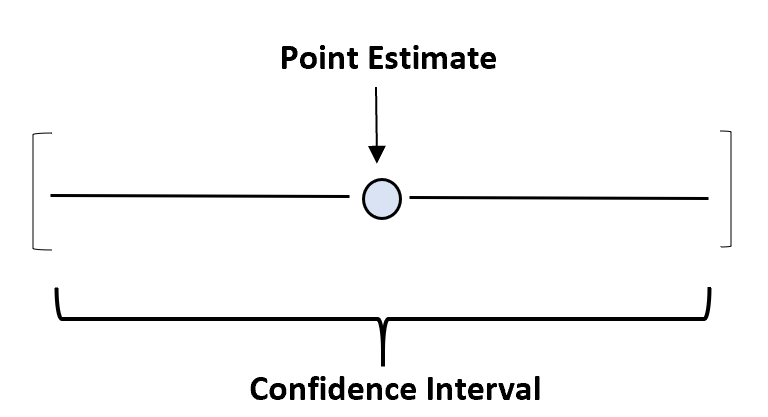
Наприклад, ми можемо використати нашу середню вагу в 150,4 фунтів, щоб оцінити справжню середню вагу виду черепахи. Тоді наш довірчий інтервал буде діапазоном значень – можливо, від 145 фунтів до 155,8 фунтів.
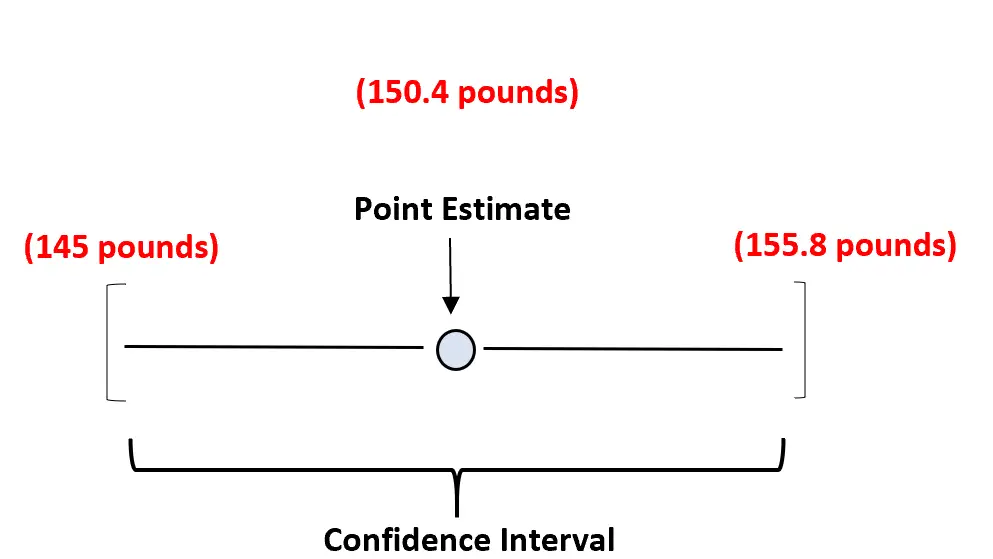
Наша точкова оцінка є нашою найкращою оцінкою справжньої середньої ваги сукупності, а довірчий інтервал надає діапазон значень, які, ймовірно, містять справжню середню вагу сукупності.
Ви можете дізнатися більше про довірчі інтервали тут .
Додаткові ресурси
Статистика проти. параметри: в чому різниця?
Населення проти зразок: яка різниця?
Вступ до довірчих інтервалів