Чому режим важливий у статистиці?
Режим представляє значення, яке найчастіше з’являється в наборі даних.
Набір даних не може мати режимів (якщо значення не повторюються), один режим або кілька режимів.
Наприклад, режим у наступному наборі даних становить 19:
Набір даних: 3, 4, 11, 15, 19 , 19, 19 , 22 , 22, 23, 23, 26
Це значення, яке зустрічається найчастіше.
У статистиці режим важливий з таких причин:
Причина 1 : це дозволяє нам знати, які значення в наборі даних є найпоширенішими.
Причина 2 : це корисно для пошуку найбільш поширених значень у категоріальних даних, коли середнє значення та медіану неможливо обчислити.
Причина 3 : це дає нам уявлення про те, де знаходиться «центр» набору даних, навіть якщо медіана та середнє використовуються частіше (як ми побачимо далі в цій статті).
Наступні приклади ілюструють кожну з цих причин на практиці.
Причина 1: Режим повідомляє нам, яке значення є найпоширенішим
Припустімо, у нас є набір даних із 100 000 рядків, що містять ціни продажу будинків у Сполучених Штатах:

Припустімо, що ми використовуємо статистичне програмне забезпечення (наприклад, Excel , R , Python тощо), щоб обчислити режим цього набору даних і виявимо, що існує три режими:
- 280 000 доларів США
- 300 000 доларів США
- 305 000 доларів США
Це одразу дає нам уявлення про найпоширеніші ціни на житло в наборі даних.
Обчислення режиму тисяч також набагато швидше, ніж перегляд рядків даних і спроба визначити, які ціни на житло зустрічаються найчастіше.
Причина 2: режим шукає найбільш поширене значення в категоріальних даних
Припустімо, що ми маємо набір даних із 1000 рядків, які повідомляють нам про колір автомобіля, що належить особам у певному районі:
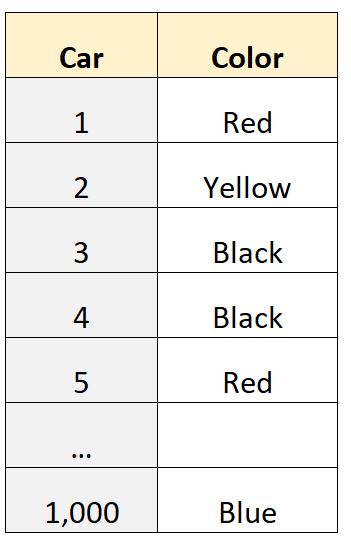
Змінна «колір» є категоріальною змінною , що означає, що значення належать до категорій («червоний», «жовтий», «чорний» тощо), і тому ми не можемо обчислити кількісне значення, наприклад середнє або медіана .
Однак ми можемо обчислити режим, оскільки він просто представляє найбільш поширене значення в наборі даних.
Наприклад, ми могли б використати статистичне програмне забезпечення, щоб визначити, що режим цього набору даних — «чорний», що говорить нам, що найпоширеніший колір автомобіля в цьому наборі даних — чорний.
Причина 3: Режим дає нам уявлення про те, де знаходиться центр набору даних
Режим також вважається мірою центральної тенденції , тобто він може дати нам уявлення про те, де знаходиться «центр» набору даних.
Наприклад, припустімо, що ми маємо такий набір даних, який показує результати іспитів 20 різних студентів у класі:

Режим виявляється 82 – це найпоширеніший бал на іспиті. Це також виявляється хорошим показником того, де в цьому наборі даних лежить «основне» значення оцінки в огляді.
Однак припустімо, що натомість ми маємо такий набір даних результатів іспиту:
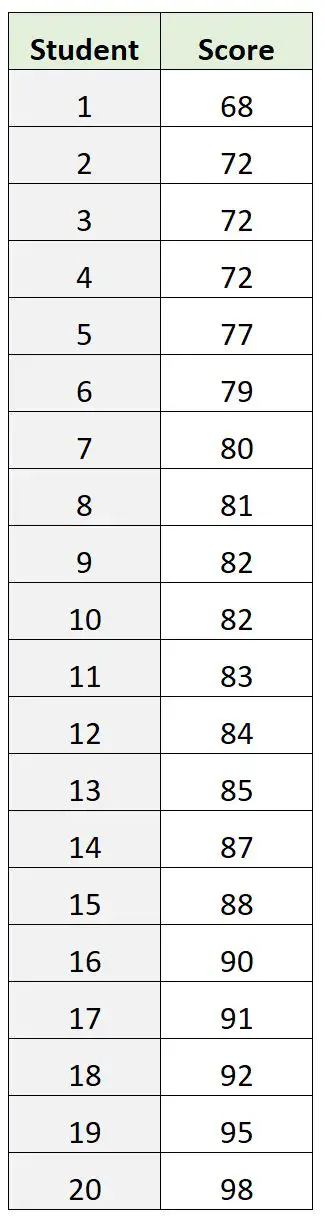
У цьому наборі даних 72 – це бал іспиту з моди. Однак це виявляється поганим показником того, де лежить «базова» оцінка іспиту.
Середній бал іспиту становить 82,9 , а середній бал іспиту – 82,5 , обидва вони дають нам краще уявлення про те, де лежить «центральне» значення по відношенню до моди.
Резюме
Ось короткий виклад основних моментів, розглянутих у цій статті:
- Режим представляє значення(-я), які найчастіше з’являються в наборі даних.
- Режим повідомляє нам найпоширеніше значення в категоричних даних, коли середнє значення та медіана не можуть бути використані.
- Режим дає нам уявлення про те, де знаходиться «центр» набору даних, але він може ввести в оману в порівнянні із середнім або медіаною.
Додаткові ресурси
У наступних посібниках надається додаткова інформація про середнє значення, медіану та режим у статистиці:
Чому середня величина важлива в статистиці?
Чому медіана важлива в статистиці?
Конкретні приклади: використання середнього значення, медіани та моди
Коли використовувати середнє проти Медіана: з прикладами