Взаємовключні або взаємовиключні події
Дві події є взаємовиключними , якщо вони не можуть відбутися одночасно.
Наприклад, припустимо, що подія A — це подія, коли кубик падає на парне число, а подія B — це подія, коли кубик падає на непарне число.
Ми б визначили вибірковий простір для подій наступним чином:
- A = {2, 4, 6}
- B = {1, 3, 5}
Зверніть увагу, що між двома вибірковими просторами немає перекриття. Таким чином, події A і B є взаємовиключними, оскільки вони не можуть відбутися одночасно. Число, на яке випадає кубик, не може бути одночасно парним і непарним.
І навпаки, дві події є взаємовключними , якщо вони можуть відбутися одночасно.
Наприклад, нехай подія C — це подія, коли кубик падає на парне число, а подія D — подія, коли кубик падає на число більше 3.
Ми б визначили вибірковий простір для подій наступним чином:
- C = {2, 4, 6}
- d = {4, 5, 6}
Зверніть увагу, що між двома вибірковими просторами є перекриття. Таким чином, події C і D є взаємовключними, оскільки вони можуть відбуватися одночасно. Гральний кубик може впасти на парне число більше 3.
Імовірності подій
Якщо дві події виключають одна одну , то ймовірність того, що вони відбудуться, дорівнює нулю.
Наприклад, розглянемо два приклади подій A і B вище:
- A = {2, 4, 6}
- B = {1, 3, 5}
Оскільки в просторах вибірки немає перекриття, ми б сказали, що P(A і B) = 0 .
Але якщо дві події взаємопов’язані , то ймовірність того, що вони відбудуться, буде числом, більшим за нуль.
Наприклад, розглянемо два приклади простору для подій C і D раніше:
- C = {2, 4, 6}
- d = {4, 5, 6}
Оскільки існує 6 можливих чисел, на які може впасти кубик, і два з цих чисел (4 і 6) належать до обох подій C і D, ми б обчислили P(C і D) як 2/6 або 1/3 .
Перегляд взаємовключних і взаємовиключних подій
Ми часто використовуємо діаграми Венна, щоб візуалізувати ймовірності, пов’язані з подіями.
Якщо дві події є взаємовиключними , вони взагалі не перекриватимуться на діаграмі Венна:
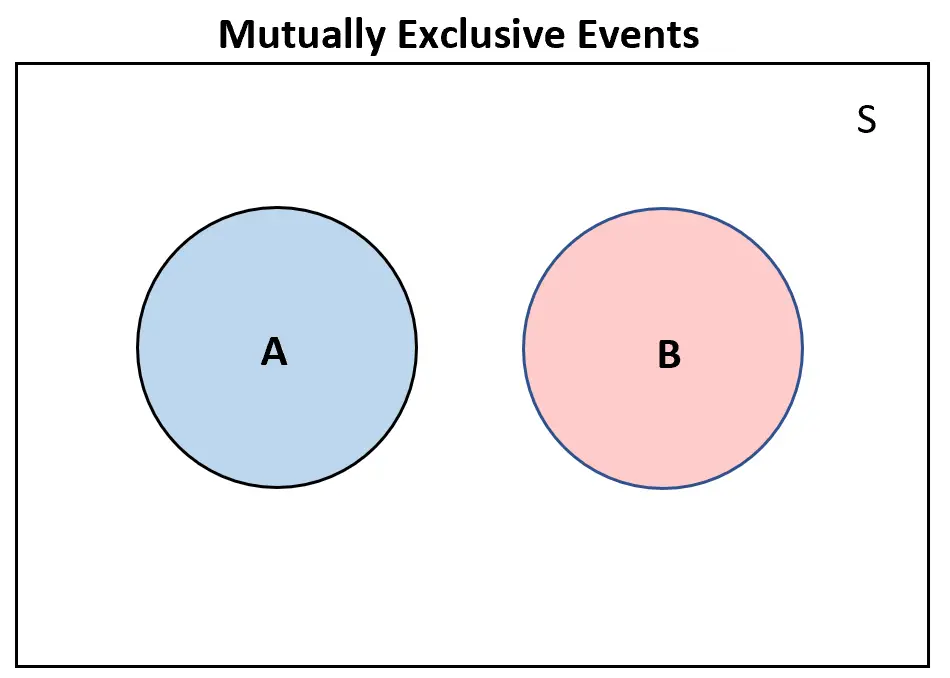
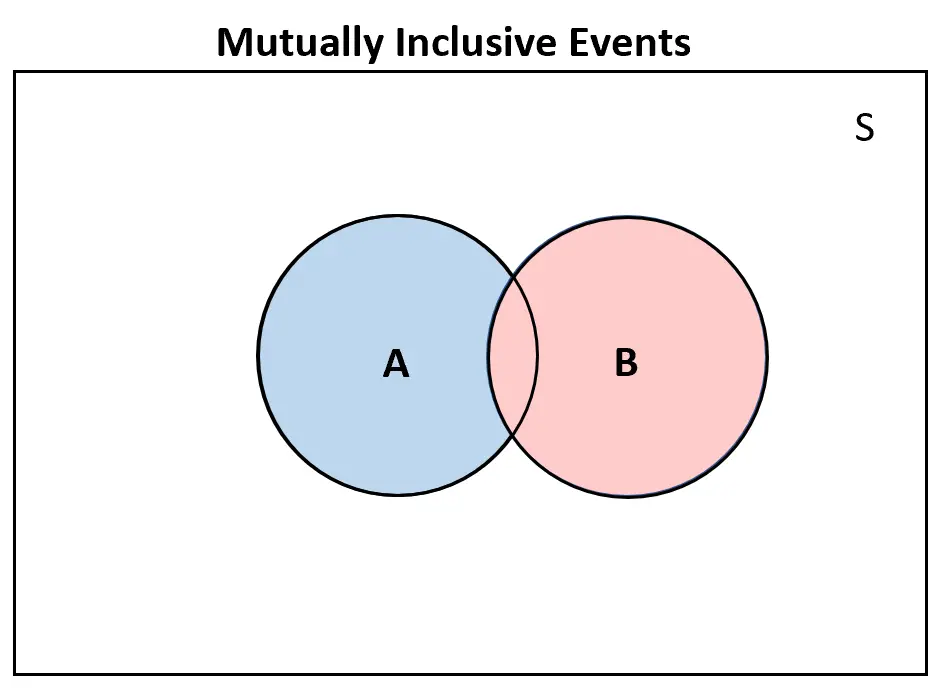
І навпаки, якщо дві події взаємно включаються , на діаграмі Венна буде принаймні деяке перекриття:
Додаткові ресурси
Вступ до теоретичної ймовірності
Загальне правило множення
Що таке непересічні події?