Міри центральної тенденції: визначення та приклади
Міра центральної тенденції – це одне значення, яке представляє центральну точку набору даних. Це значення також можна назвати «центральним розташуванням» набору даних.
У статистиці існує три загальні показники центральної тенденції:
- Середня
- Медіана
- Мода
Кожен із цих заходів визначає центральне розташування набору даних різними методами. Залежно від типу даних, які ви аналізуєте, краще використовувати один із цих трьох показників, а не два інших.
У цій статті ми розглянемо, як обчислити кожен із трьох показників центральної тенденції, а також як визначити, який показник найкраще використовувати на основі ваших даних.
Чому міри центральної тенденції корисні?
Перш ніж ми розглянемо, як обчислити середнє, медіану та моду, корисно зрозуміти , чому ці вимірювання насправді корисні.
Розглянемо такий сценарій:
Молода пара намагається вирішити, де купити свій перший будинок у новому місті, і щонайбільше вони можуть витратити 150 000 доларів. У деяких районах міста є дорогі будинки, в інших – дешеві, а в деяких – будинки середньої ціни. Вони хочуть легко звузити свій пошук до конкретних районів, які відповідають їх бюджету.
Якби подружжя просто подивилося на ціни на односімейні будинки в кожному районі, у них могли б виникнути труднощі з визначенням, які райони найкраще відповідають їхньому бюджету, оскільки вони могли б побачити щось подібне:
Ціни на будинки в районі А : $140 000, $190 000, $265 000, $115 000, $270 000, $240 000, $250 000, $180 000, $160 000, $200 000, $240 000, $280 000,…
Ціни на будинки в районі Б : 140 000, 290 000, 155 000, 165 000, 280 000, 220 000, 155 000, 185 000, 160 000, 200 000, 190 000, 140 000, 145 доларів. 00 0,…
Ціни на будинки в районі C : $140 000, $130 000, $165 000, $115 000, $170 000, $100 000, $150 000, $180 000, $190 000, $120 000, $110 000, $130 000, $120, 00 0,…
Однак, якби вони знали середню ціну (наприклад, показник центральної тенденції) будинків у кожному районі, тоді вони могли б уточнити свій пошук набагато швидше, оскільки вони могли б легше визначити, у якому районі ціни на будинки відповідають їх бюджету:
Середня ціна будинку в районі А: 220 000 доларів
Середня ціна будинку в районі B : 190 000 доларів
Середня ціна будинку в районі C : 140 000 доларів
Знаючи середню ціну на житло в кожному районі, вони можуть швидко побачити, що в мікрорайоні С , ймовірно, буде найбільше доступних будинків у межах їх бюджету.
Це перевага використання вимірювання центральної тенденції: це допомагає вам зрозуміти центральне значення набору даних, яке, як правило, описує, де зазвичай лежать значення даних. У цьому конкретному прикладі це допомагає молодій парі зрозуміти типову ціну будинку в кожному районі.
Висновок: вимірювання центральної тенденції є корисним, оскільки воно дає нам єдине значення, яке описує «центр» набору даних. Це допомагає нам зрозуміти набір даних набагато швидше, ніж просто переглядати всі окремі значення в наборі даних.
Середній
Найбільш часто використовуваним показником центральної тенденції є середнє значення . Щоб обчислити середнє значення набору даних, просто складіть усі окремі значення та розділіть на загальну кількість значень.
Середнє = (сума всіх значень) / (загальна кількість значень)
Наприклад, припустімо, що ми маємо такий набір даних, який показує кількість хоум-ранів, зроблених 10 бейсболістами однієї команди протягом сезону:
| гравець | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #десять |
|---|---|---|---|---|---|---|---|---|---|---|
| Хоум-рани | 8 | 15 | 22 | 21 | 12 | 9 | 11 | 27 | 14 | 13 |
Середню кількість хоум-ранів, виконаних на гравця, можна розрахувати наступним чином:
Середнє = (8+15+22+21+12+9+11+27+14+13) / 10 = 15,2 контурів .
Медіана
Медіана – це середнє значення набору даних. Ви можете знайти медіану, впорядкувавши всі окремі значення в наборі даних від найменшого до найбільшого та знайшовши медіанне значення. Якщо кількість значень непарна, медіана є середнім значенням. Якщо кількість значень парна, медіана є середнім з двох середніх значень.
Наприклад, щоб знайти середню кількість хоум-ранів, виконаних 10 бейсболістами в попередньому прикладі, ми можемо ранжувати гравців у порядку спадання кількості хоум-ранів:
| гравець | #1 | #6 | #7 | #5 | #десять | #9 | #2 | #4 | #3 | #8 |
|---|---|---|---|---|---|---|---|---|---|---|
| Хоум-рани | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 21 | 22 | 27 |
Оскільки ми маємо парну кількість значень, медіана є просто середнім із двох середніх значень: 13,5 .
Натомість подумайте, якби у нас було дев’ять гравців:
| гравець | #1 | #6 | #7 | #5 | #9 | #2 | #4 | #3 | #8 |
|---|---|---|---|---|---|---|---|---|---|
| Хоум-рани | 8 | 9 | 11 | 12 | 14 | 15 | 21 | 22 | 27 |
У цьому випадку, оскільки ми маємо непарну кількість значень, медіана є просто середнім значенням: 14 .
Мода
Режим — це значення, яке найчастіше зустрічається в наборі даних. Набір даних не може мати режимів (якщо значення не повторюються), один режим або кілька режимів.
Наприклад, такий набір даних не має режиму:
| гравець | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #десять |
|---|---|---|---|---|---|---|---|---|---|---|
| Хоум-рани | 8 | 9 | 11 | 12 | 13 | 14 | 15 | 21 | 22 | 27 |
Наступний набір даних має режим: 15 . Це значення, яке з’являється найчастіше.
| гравець | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #десять |
|---|---|---|---|---|---|---|---|---|---|---|
| Хоум-рани | 8 | 9 | 11 | 12 | 13 | 15 | 15 | 21 | 22 | 27 |
Наступний набір даних має три режими: 8, 15, 19 . Це значення, які з’являються найчастіше.
| гравець | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #десять |
|---|---|---|---|---|---|---|---|---|---|---|
| Хоум-рани | 8 | 8 | 11 | 12 | 15 | 15 | 17 | 19 | 19 | 27 |
Режим може бути особливо корисним показником центральної тенденції під час роботи з категоріальними даними, оскільки він повідомляє нам, яка категорія з’являється найчастіше. Наприклад, розглянемо наступну гістограму, яка показує результати опитування про улюблений колір людей:
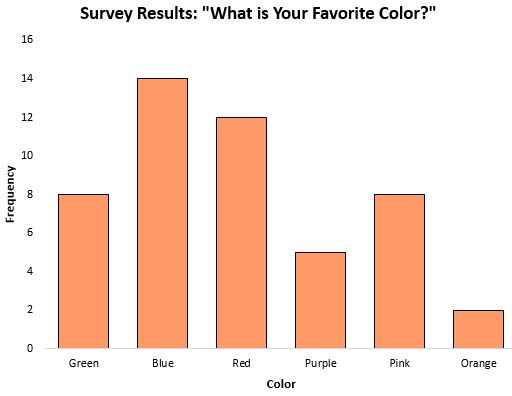
Режим або відповідь, яка траплялася найчастіше, була синього кольору.
У сценаріях, де дані є категоричними (як у наведеному вище), неможливо навіть обчислити медіану чи середнє значення, тому режим є єдиним показником центральної тенденції, який ми можемо використовувати.
Режим також можна використовувати для числових даних, як ми бачили у прикладі вище з бейсбольними гравцями. Однак режим, як правило, менш корисний для відповіді на запитання “Яке типове значення для цього набору даних?” »
Наприклад, припустімо, що ми хочемо знати типову кількість хоум-ранів, зроблених бейсболістом цієї команди:
| гравець | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #десять |
|---|---|---|---|---|---|---|---|---|---|---|
| Хоум-рани | 8 | 8 | 11 | 12 | 15 | 15 | 17 | 19 | 19 | 27 |
Режим для цього набору даних — 8, 15 і 19, оскільки це найчастіші значення. Однак це не дуже допомагає зрозуміти типову кількість хоум-ранів, зроблених гравцем команди. Кращим показником центральної тенденції в цьому випадку буде медіана (15) або середнє (також 15).
Режим також є поганим показником центральної тенденції, коли це число далеке від решти значень. Наприклад, наступний режим набору даних становить 30, але насправді це не є «типовою» кількістю хоумранів на гравця в команді:
| гравець | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #десять |
|---|---|---|---|---|---|---|---|---|---|---|
| Хоум-рани | 5 | 6 | 7 | десять | 11 | 12 | 13 | 15 | 30 | 30 |
Знову ж таки, середнє або медіана краще описуватимуть центральне розташування цього набору даних.
Коли використовувати середнє значення, медіану та режим
Ми бачили, що середнє значення, медіана та мода вимірюють центральне розташування або «типове значення» набору даних дуже різними способами:
Середнє: знаходить середнє значення в наборі даних.
Медіана: знаходить середнє значення в наборі даних.
Режим: знаходить найбільш часте значення в наборі даних.
Ось сценарії, у яких певні показники центральної тенденції краще використовувати, ніж інші:
Коли використовувати середнє значення
Найкраще використовувати середнє значення, коли розподіл даних досить симетричний і немає викидів.
Наприклад, припустімо, що ми маємо такий розподіл, який показує зарплати окремих людей у певному місті:

Оскільки цей розподіл досить симетричний (тобто, якщо ви розділите його навпіл, кожна половина виглядатиме приблизно рівною) і немає викидів (тобто (скажімо, немає надзвичайно високих зарплат), середнє значення буде добре описувати цей набір даних.
Середня сума становить 63 000 доларів США, що знаходиться приблизно в центрі розподілу:

Коли використовувати медіану
Найкраще використовувати медіану, коли розподіл даних спотворений або коли є викиди.
Упереджені дані:
Коли розподіл спотворений, медіані все одно вдається охопити центральне розташування. Для прикладу розглянемо такий розподіл зарплат окремих осіб у певному місті:

Медіана краще відображає «типову» зарплату особи, ніж середня. Це пояснюється тим, що великі значення в хвості розподілу мають тенденцію переміщувати середнє значення від центру до довгого хвоста.
У цьому конкретному прикладі середнє значення говорить нам, що типова людина заробляє приблизно 47 000 доларів США на рік у цьому місті, тоді як медіана говорить нам, що типова особа заробляє лише близько 32 000 доларів США на рік, що є набагато більш репрезентативним для типової особи.
Викиди:
Медіана також допомагає краще охопити центральне розташування розподілу, коли в даних є викиди. Наприклад, розглянемо наступний графік, який показує площу будинків на певній вулиці:

На середнє значення сильно впливають кілька надзвичайно великих будинків, а на медіану – ні. Таким чином, медіана краще фіксує «типову» площу будинку на цій вулиці, ніж середня.
Коли використовувати режим
Цей режим найкраще використовувати, коли ви працюєте з категоріальними даними і хочете знати, яка категорія з’являється найчастіше. Ось кілька прикладів:
- Ви проводите опитування про улюблені кольори людей і хочете знати, який колір найчастіше зустрічається у відповідях.
- Ви проводите опитування щодо вподобань людей серед трьох варіантів дизайну веб-сайту та хочете знати, який дизайн люди віддають перевагу найбільше.
Як згадувалося раніше, якщо ви працюєте з категоріальними даними, неможливо навіть обчислити медіану чи середнє значення, що залишає моду єдиною мірою центральної тенденції.
Загалом, якщо ви працюєте з числовими даними, такими як квадратні метри будинків, кількість хоум-ранів на гравця, зарплата на особу тощо, зазвичай найкраще використовувати медіану або середнє для опису значення «типове» в набір даних.
Примітка. Важливо зауважити, що якщо набір даних повністю розподілено нормально, то середнє значення, медіана та мода мають однакове значення.