Відносна частота

за Редакція 4 Серпня, 2023 Статистика 0 коментарів

У цій статті ви дізнаєтесь, що таке відносна частота в статистиці, як отримати відносну частоту та розв’яжете дві покрокові вправи щодо відносної частоти.

Що таке відносна частота?

У статистиці відносна частота – це міра, яка вказує кількість разів, коли значення з’являється у вибірці даних як пропорція або відсоток. Точніше, відносна частота дорівнює абсолютній частоті, поділеній на загальну кількість даних.

Наприклад, якщо абсолютна частота значення дорівнює 15 і загалом є 100 точок даних, відносна частота цього значення дорівнює 0,15 (15/100=0,15).

Як правило, символ h _i використовується для представлення відносної частоти. Хоча в статистичній спільноті досі немає консенсусу, тому ви можете побачити відносну частоту, представлену іншим символом.

Як розрахувати відносну частоту

Відносна частота дорівнює абсолютній частоті, поділеній на загальну кількість даних. Тому, щоб обчислити відносну частоту, потрібно спочатку знайти абсолютну частоту, а потім розділити її на загальну кількість спостережень.

Отже, формула для відносної частоти така:

$h_i=\cfrac{f_i}{N}$

золото:

$h_i$

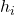
є відносною частотою.
$f_i$

– абсолютна частота.
$N$

це загальна кількість даних.

З іншого боку, щоб обчислити відносну частоту у відсотках , тобто відносну частоту, виражену у відсотках, просто помножте попередню формулу на 100:

$h_i (\%)=\cfrac{f_i}{N}\cdot 100$

Приклади відносної частоти

Ознайомившись із визначенням відносної частоти, нижче наведено два реальні приклади, щоб ви могли побачити, як обчислюється цей тип частоти. У першому прикладі визначається відносна частота дискретної змінної, а в другому – безперервної змінної.

Приклад 1: дискретна змінна

Оцінки, отримані з предмету статистика у класі, який налічує 30 учнів, такі. Яка відносна частота кожної ноти?

$5\ 4\ 7\ 9\ 10\ 6\ 7\ 4\ 8\ 3$

$6\ 9\ 8\ 5\ 6\ 4\ 6\ 2\ 4\ 7$

$8\ 9\ 10\ 5\ 4\ 3\ 6\ 8\ 7\ 5$

Змінна в цій вправі є дискретною, оскільки дані можуть бути лише цілими; отже, немає необхідності групувати дані в інтервали.

Щоб знайти відносну частоту, ми повинні спочатку визначити абсолютну частоту. Тому ми будуємо таблицю частот і обчислюємо абсолютну частоту для кожного окремого значення:

➤ Дивіться: як розрахувати абсолютну частоту

Тепер, коли ми обчислили абсолютну частоту, ми можемо обчислити відносну частоту. Для цього просто розділіть кожну абсолютну частоту на загальну кількість даних (30):

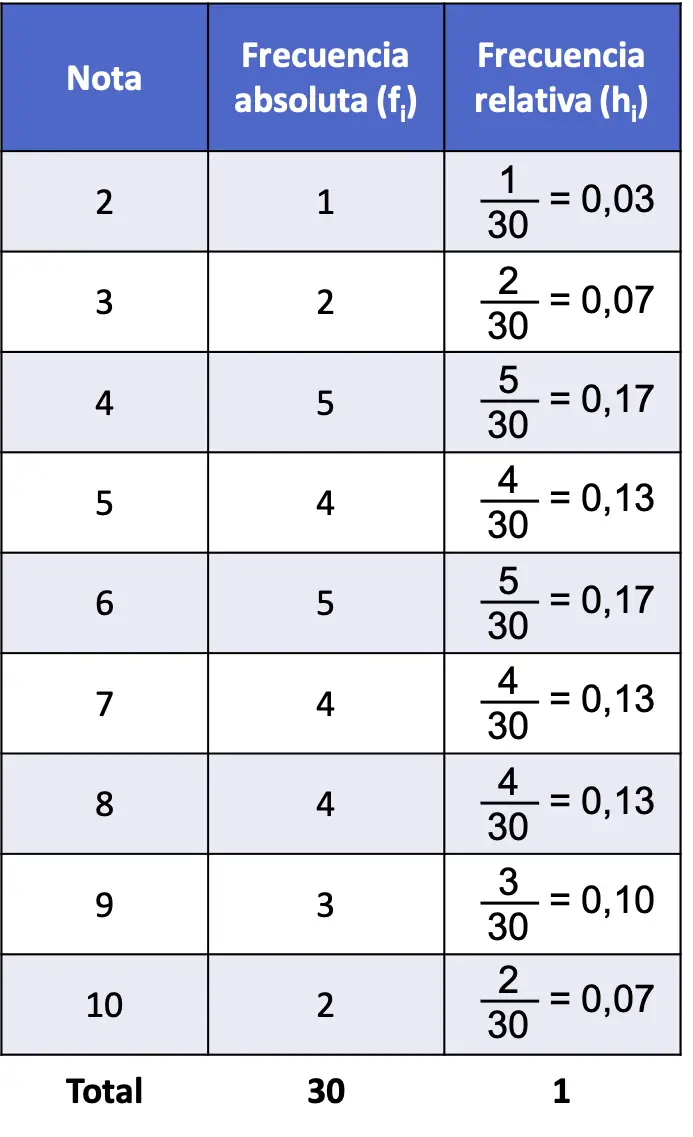
Отже, частотна таблиця проблеми з абсолютною частотою і відносною частотою виглядає наступним чином:

Зверніть увагу, що сума всіх відносних частот завжди дає 1, інакше це означає, що деякі розрахунки неправильні.

Приклад 2: безперервна змінна

Було виміряно зріст 20 людей і отримано результати, зазначені нижче. Розділіть дані на інтервали та знайдіть відносну частоту кожного інтервалу.

$1,84\ 1,71\ 1,75\ 1,92\ 1,57\ 1,67\ 1,94\ 1,83\ 1,79\ 1,68$

$1,54\ 1,61\ 1,78\ 1,62\ 1,89\ 1,80\ 1,99\ 1,77\ 1,70\ 1,63$

Дані в цій статистичній вибірці належать до безперервної змінної, оскільки вони є десятковими і тому змінна може приймати будь-яке значення. Отже, перед тим, як виконувати обчислення частоти, ми спочатку згрупуємо дані в інтервали з амплітудою 10 десятих.

Далі складаємо частотну таблицю з абсолютною частотою кожного інтервалу:

абсолютна частота для даних, згрупованих в інтервали

І як тільки ми знайдемо абсолютну частоту, ми можемо отримати відносну частоту кожного інтервалу, поділивши його абсолютну частоту на загальну кількість даних (20):

відносна частота для даних, згрупованих в інтервали

Кумулятивна відносна частота

Як випливає з назви, кумулятивна відносна частота — це інший тип частоти, який використовується в статистиці та обчислюється на основі відносної частоти.

Точніше, кумулятивна відносна частота значення дорівнює сумі відносної частоти самого значення плюс відносні частоти всіх менших значень.

Щоб ви могли побачити, як отримано кумулятивну відносну частоту, кумулятивну відносну частоту набору даних у першому прикладі було розраховано нижче:

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше