Гетероскедастичність

У цій статті пояснюється, що таке гетероскедастичність у статистиці. Крім того, ви дізнаєтесь, що викликає гетероскедастичність, які її наслідки та як її виправити.

Що таке гетероскедастичність?

У статистиці гетероскедастичність — це характеристика, яка представляє модель регресії, яка означає, що дисперсія помилки не є постійною. Іншими словами, гетероскедастична модель означає, що її помилки мають нерегулярну дисперсію, тоді модель називається гетероскедастичною.

Пам’ятайте, що помилка (або залишок) визначається як різниця між реальним значенням і значенням, оціненим регресійною моделлю.

При побудові регресійної моделі помилка кожного спостереження обчислюється за допомогою попереднього виразу. Таким чином, статистична модель є гетероскедастичною, коли дисперсія обчислених помилок не є постійною протягом спостережень, а змінюється.

Хоча це може здатися дуже простим, важливо, щоб модель регресії не представляла гетероскедастичності, оскільки розрахунок моделі базується на тому факті, що дисперсія залишків є постійною, фактично це одне з попередніх припущень регресійні моделі.

Існують певні статистичні тести, які можуть виявити гетероскедастичність, такі як тест Уайта або тест Голдфельда-Квандта. Однак, як правило, шляхом побудови залишків можна визначити їх гетероскедастичність.

Причини гетероскедастичності

Найпоширенішими причинами гетероскедастичності в моделі є:

• Коли діапазон даних дуже широкий порівняно із середнім. Якщо в одній і тій же статистичній вибірці є дуже великі значення та дуже малі значення, ймовірно, що отримана регресійна модель є гетероскедатичною.
• Виключення змінних у регресійній моделі також призводить до гетероскедастичності. Логічно, що якщо відповідна змінна не включена в модель, її варіація буде включена в залишки, і це не обов’язково буде виправлено.
• Подібним чином зміна структури може призвести до поганої відповідності моделі набору даних, і, отже, дисперсія залишків може бути непостійною.
• Коли деякі змінні мають набагато більші значення, ніж інші пояснювальні змінні, модель може мати гетероскедастичність. У цьому випадку змінні можна релятивізувати, щоб вирішити проблему.

Однак деякі випадки за своєю природою можуть демонструвати гетероскедастичність. Наприклад, якщо ми змоделюємо дохід людини з її витратами на їжу, багатші люди матимуть набагато більшу мінливість у своїх витратах на їжу, ніж бідні люди. Тому що багата людина їсть іноді в дорогих ресторанах, а іноді в дешевих, на відміну від бідної людини, яка завжди їсть в дешевих ресторанах. Таким чином, регресійній моделі легко мати гетероскедастичність.

Наслідки гетероскедастичності

Головним чином, наслідки гетероскедастичності в регресійній моделі такі:

• Ефективність втрачається в оцінці методом найменших квадратів, визначеній як середнє квадратів помилок.
• Виникають помилки при обчисленні коваріаційної матриці оцінок методів найменших квадратів.

Правильна гетероскедастичність

Коли результуюча регресійна модель є гетероскедастичною, ми можемо спробувати такі поправки, щоб отримати гетероскедастичність:

• Обчисліть натуральний логарифм незалежної змінної, це зазвичай корисно, коли дисперсія залишків збільшується на графіку.
• Залежно від залишкового графіка інший тип перетворення незалежної змінної може бути більш практичним. Наприклад, якщо графік має форму параболи, ми можемо обчислити квадрат незалежної змінної та додати цю змінну до моделі.
• Для моделі також можна використовувати інші змінні; шляхом видалення або додавання змінної дисперсія залишків може бути змінена.
• Замість використання критерію найменших квадратів можна використовувати зважений критерій найменших квадратів.

Гетероскедастичність і гомоскедастичність

Нарешті, ми побачимо, які відмінності між гетероскедастичністю та гомоскедастичністю в статистиці, оскільки це дві концепції регресійних моделей, про які ми повинні чітко знати.

Гомоскедастичність регресійної моделі є статистичною характеристикою, яка вказує на постійність дисперсії помилки. Таким чином, гомоскедастична модель означає, що дисперсія її помилок постійна.

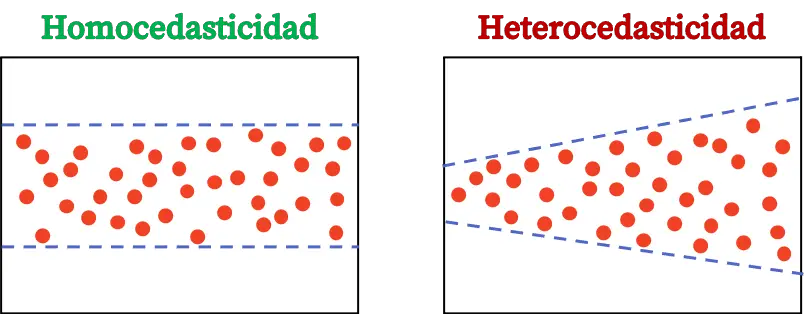
Різниця між гетероскедастичністю та гомоскедастичністю полягає в сталості дисперсії залишків. Якщо дисперсія залишків моделі непостійна, це означає, що модель гетероскедастична. З іншого боку, якщо дисперсія залишків постійна, це означає, що вона гомоскедастична.

Тому нам потрібно переконатися, що регресійна модель, яку ми будуємо, є гомоскедастичною, таким чином буде виконано припущення про те, що дисперсія залишків є постійною.