Повний посібник: як перевірити припущення manova

MANOVA (багатофакторний дисперсійний аналіз) використовується для аналізу того, як одна або більше факторних змінних впливають на множинні змінні відповіді.

Наприклад, ми могли б використати MANOVA, щоб проаналізувати, як рівень освіти (диплом середньої школи, ступінь молодшого спеціаліста, ступінь бакалавра, ступінь магістра) впливає як на річний дохід, так і на загальну заборгованість по студентській позиці.

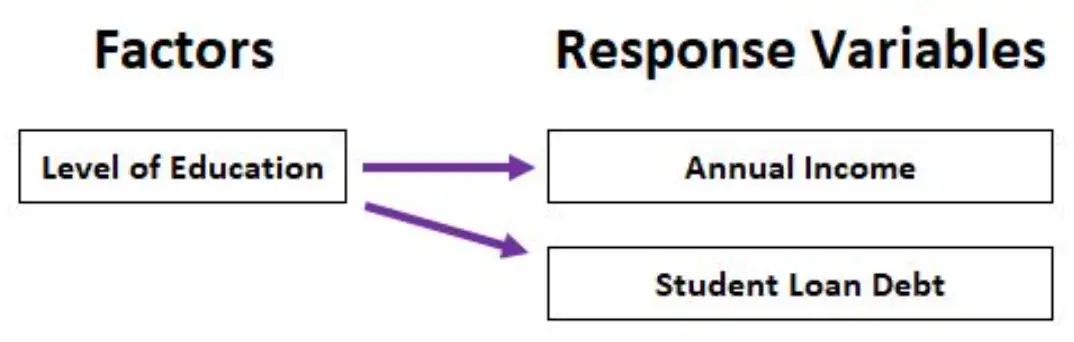
Пов’язане: відмінності між ANOVA, ANCOVA, MANOVA та MANCOVA

Кожного разу, коли ми виконуємо MANOVA, ми повинні перевірити, чи виконуються такі припущення:

1. Багатовимірна нормальність – Змінні відповіді є багатовимірними, нормально розподіленими в кожній групі факторних змінних.

2. Незалежність – кожне спостереження випадково та незалежно відібрано з популяції.

3. Рівна дисперсія – Матриці коваріацій сукупності кожної групи рівні.

4. Немає багатовимірних викидів – немає екстремальних багатовимірних викидів.

У цій статті ми пояснюємо кожне припущення, а також пояснюємо, як визначити, чи виконується це припущення.

Припущення 1: Багатовимірна нормальність

MANOVA припускає, що змінні відповіді є багатовимірними, нормально розподіленими в кожній групі факторної змінної.

Якщо є принаймні 20 спостережень для кожної комбінації факторів * змінних відповіді, тоді можна вважати, що припущення багатофакторної нормальності виконується.

Якщо є менше 20 спостережень для кожної комбінації змінної фактора*відповіді, ми можемо створити матрицю розсіювання, щоб візуалізувати залишки та візуально перевірити, чи виконується це припущення.

На щастя, добре відомо, що MANOVA є стійкою до відхилень від багатофакторної нормальності, тому малі та помірні відхилення, як правило, не є проблемою.

Гіпотеза 2: Незалежність

MANOVA припускає, що кожне спостереження випадково та незалежно відібрано з популяції.

Якщо для збору даних використовується метод ймовірнісної вибірки (кожен член сукупності має однакову ймовірність бути відібраним до вибірки), ми можемо припустити, що кожне спостереження було відібрано випадковим і незалежним способом.

Приклади методів ймовірнісної вибірки включають:

• Проста випадкова вибірка
• Стратифікована випадкова вибірка
• Випадкова кластерна вибірка
• Систематична випадкова вибірка

Припущення 3: однакова дисперсія

MANOVA передбачає, що коваріаційні матриці сукупності кожної групи рівні.

Найпоширенішим способом перевірки цієї гіпотези є використання М-тесту Бокса. Відомо, що цей тест є досить суворим, тому ми зазвичай використовуємо рівень значущості 0,001, щоб визначити, чи рівні коваріаційні матриці сукупності чи ні.

Якщо p-значення тесту М Бокса більше 0,001, ми можемо вважати, що це припущення виконується.

На щастя, навіть якщо p-значення тесту менше 0,001, MANOVA має тенденцію бути стійким до відхилень від цієї гіпотези.

Щоб нерівні коваріаційні матриці були проблемою, відмінності між коваріаційними матрицями мають бути досить екстремальними.

Гіпотеза 4: відсутність багатовимірних викидів

MANOVA припускає, що в даних немає екстремальних багатофакторних викидів, які могли б суттєво вплинути на результати.

Найпоширенішим способом перевірки цього припущення є обчислення відстані Махаланобіса для кожного спостереження, яке представляє відстань між двома точками в багатовимірному просторі.

Якщо відповідне значення p для відстані Махаланобіса спостереження менше 0,001, ми зазвичай оголошуємо це спостереження екстремальним викидом.

Зверніться до наступних посібників, щоб дізнатися, як обчислити відстань Махаланобіса в різних статистичних програмах:

• Як розрахувати відстань Махаланобіса в R
• Як обчислити відстань Махаланобіса в SPSS
• Як обчислити відстань Махаланобіса в Python

Додаткові ресурси

У наступних посібниках пояснюється, як виконати MANOVA в різних статистичних програмах:

Як виконати MANOVA в R
Як виконати MANOVA у SPSS
Як виконати MANOVA в Stata