Як аналізувати залишки в моделі anova
ANOVA («дисперсійний аналіз») — це тип моделі, який використовується для визначення того, чи існує значна різниця між середніми значеннями трьох або більше незалежних груп.
ми підбираємо дисперсійний аналіз Кожного разу, коли модель до набору даних, завжди будуть залишки – вони представляють різницю між кожним окремим спостереженням і груповим середнім значенням, з якого отримано спостереження.
У наступному прикладі показано, як на практиці обчислити залишки для моделі ANOVA.
Приклад: обчислення залишків у ANOVA
Припустімо, ми набираємо 90 людей для участі в експерименті зі схуднення, у якому ми випадковим чином призначаємо 30 осіб для виконання Програми A, Програми B або Програми C протягом місяця.
Ми можемо виконати односторонній дисперсійний аналіз, щоб визначити, чи є статистично значуща різниця між втратою ваги в результаті трьох програм.
Припустімо, ми обчислюємо середню втрату ваги осіб, які беруть участь у кожній програмі, таким чином:
- Програма А : 1,58 фунта
- Програма B : 2,56 фунта
- Програма C : 4,13 фунта
Залишки моделі ANOVA будуть різницею між втратою ваги кожної особи та середньою втратою ваги за програмою.
Наприклад, у наведеній нижче таблиці показано, як обчислити залишки для 10 різних осіб у дослідженні:
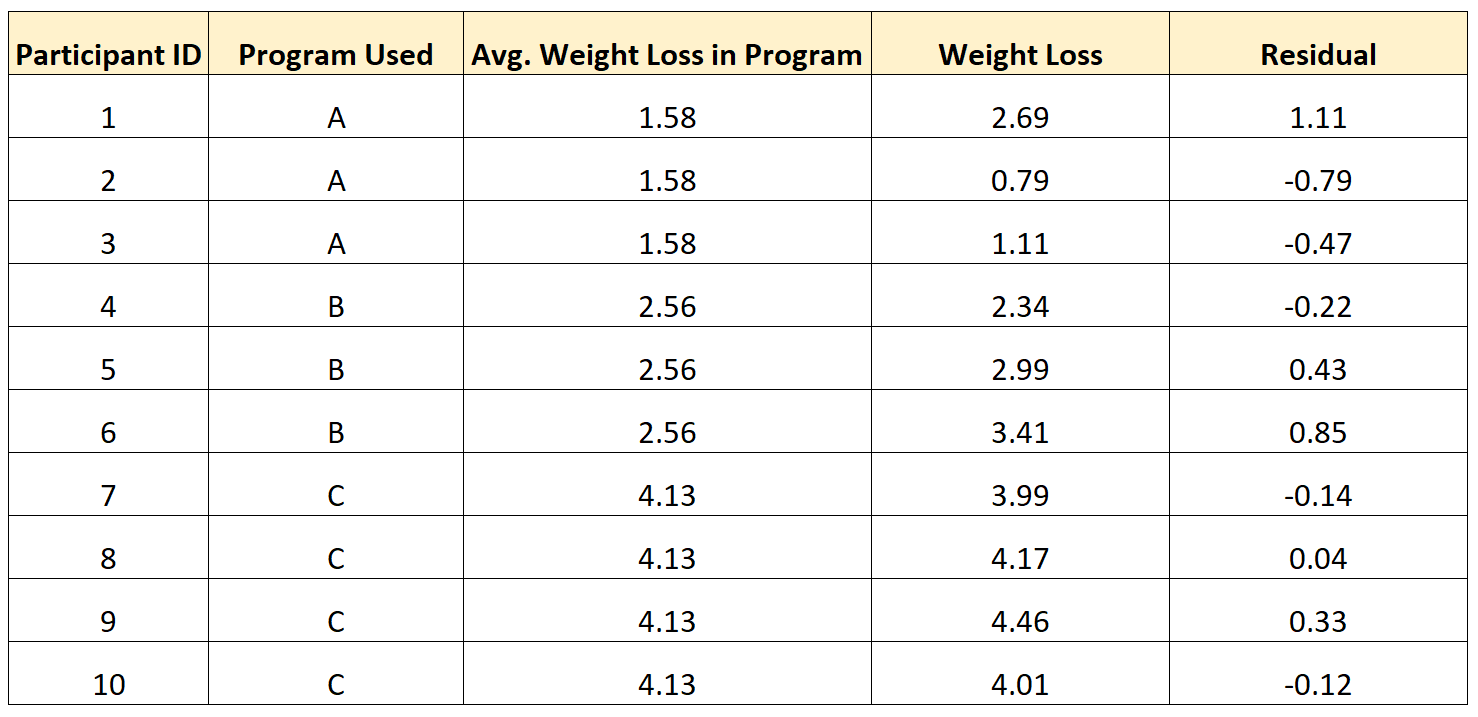
Зверніть увагу на такий шаблон:
- Особи, які мали значення вище середнього по групі, мали позитивний залишок .
- Особи, які мали значення, нижче за середнє для своєї групи, мали від’ємний залишок .
На практиці ми б обчислили залишки для всіх 90 осіб.
Як використовувати залишки для перевірки нормальності
Одним із припущень ANOVA є те, що залишки розподілені нормально.
Найпоширенішим способом перевірки цього припущення є створення графіка QQ .
Якщо залишки розподілені нормально, то точки на графіку QQ лежатимуть на прямій діагональній лінії.
Ось як виглядав би графік QQ для нашого попереднього прикладу:
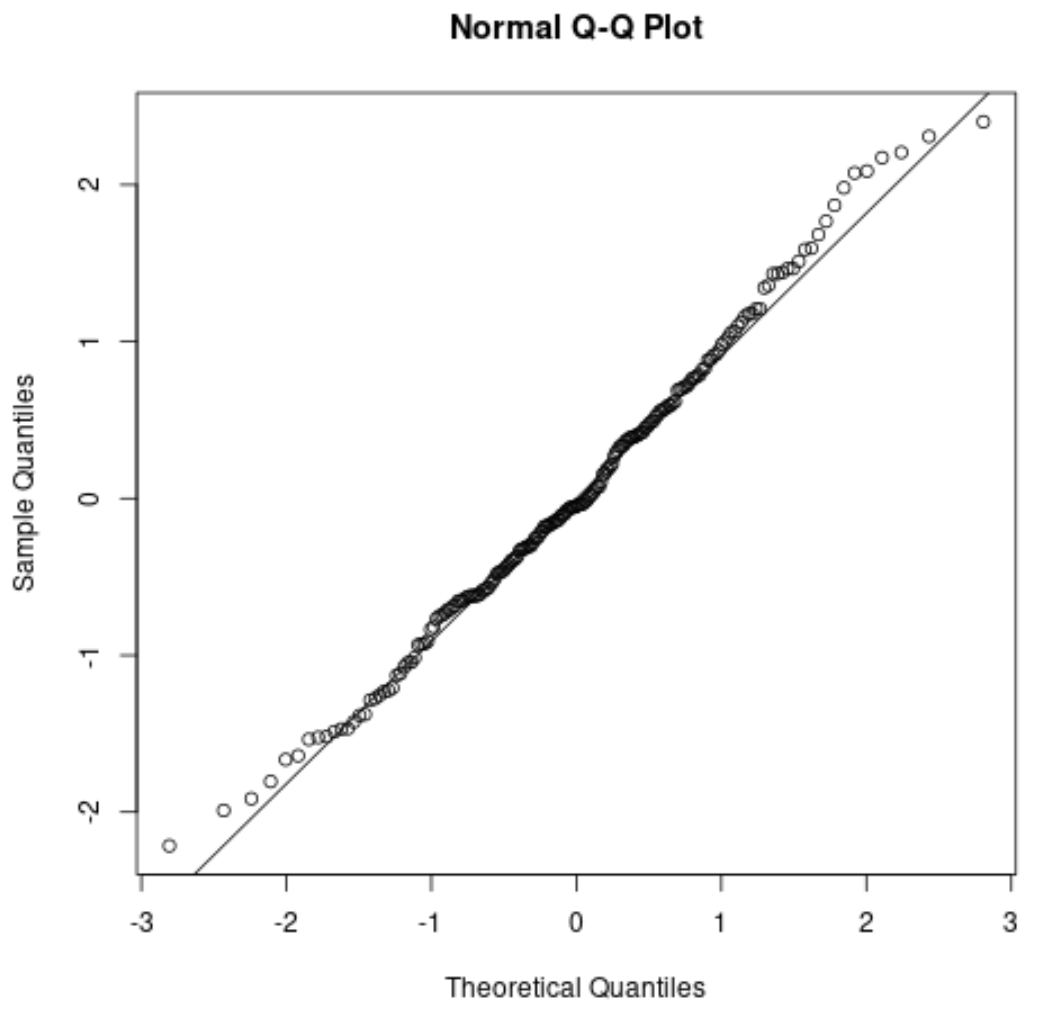
Кінчики трохи відхиляються від прямої діагональної лінії на кінцях хвоста, але в цілому спад кінчиків досить добре повторює діагональ. Це говорить нам про те, що припущення про нормальність, ймовірно, виконується.
Для довідки, ось як може виглядати графік QQ для ненормально розподілених залишків:
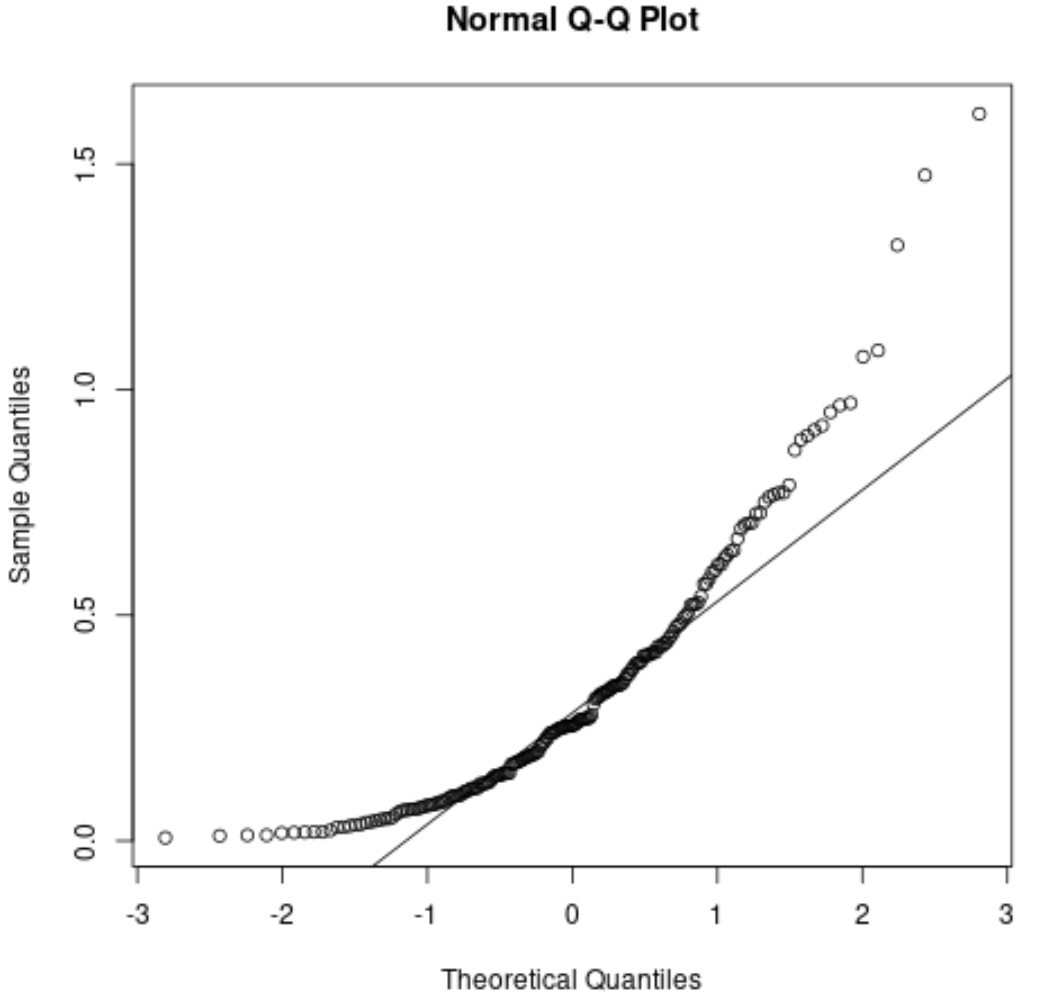
Точки сильно відхиляються від прямої діагональної лінії, що вказує на те, що залишки не розподілені нормально.
Зверніться до наступних посібників, щоб дізнатися, як створювати діаграми QQ у різному програмному забезпеченні:
Додаткові ресурси
У наступних статтях надається додаткова інформація про моделі ANOVA:
Вступ до одностороннього дисперсійного аналізу
Як перевірити припущення ANOVA
4 приклади використання ANOVA в реальному житті
Про автора
Редакція
Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше