Як виконати двовибірковий t-тест у stata
Двовибірковий t-критерій використовується, щоб перевірити, чи рівні середні дві сукупності чи ні.
У цьому підручнику пояснюється, як виконати двовибірковий t-тест у Stata.
Приклад: двовибірковий t-тест у Stata
Дослідники хочуть знати, чи нова обробка палива спричиняє зміну середньої витрати миль на галон певного автомобіля. Щоб перевірити це, вони проводять експеримент, у якому 12 автомобілів отримують нове паливо, а 12 – ні.
Виконайте наступні кроки, щоб виконати t-тест із двома зразками, щоб визначити, чи є різниця в середньому милі на галон між цими двома групами.
Крок 1. Завантажте дані.
Спочатку завантажте дані, ввівши use https://www.stata-press.com/data/r13/fuel3 у полі команди та натиснувши Enter.
Крок 2. Перегляньте необроблені дані.
Перш ніж виконувати двовибірковий t-тест, давайте спочатку подивимося на вихідні дані. У верхній панелі меню перейдіть до Дані > Редактор даних > Редактор даних (Огляд) . Перший стовпець, mpg , відображає милі на галон для даного автомобіля. Другий стовпець, підданий обробці , вказує на те, чи оброблено автомобіль паливом (0 = ні, 1 = так).
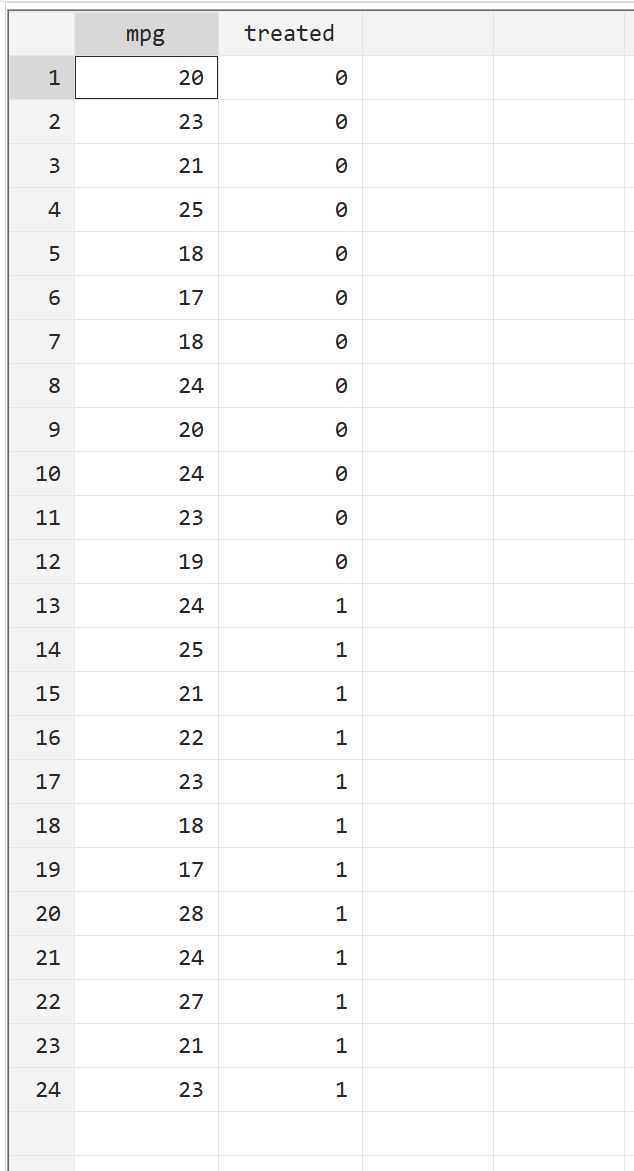
Крок 3: Візуалізуйте дані.
Далі візуалізуємо дані. Ми створимо коробкові діаграми для відображення розподілу значень миль на галон для кожної групи.
У верхній панелі меню перейдіть до Діаграми > Коробчатий графік . У змінних виберіть mpg :
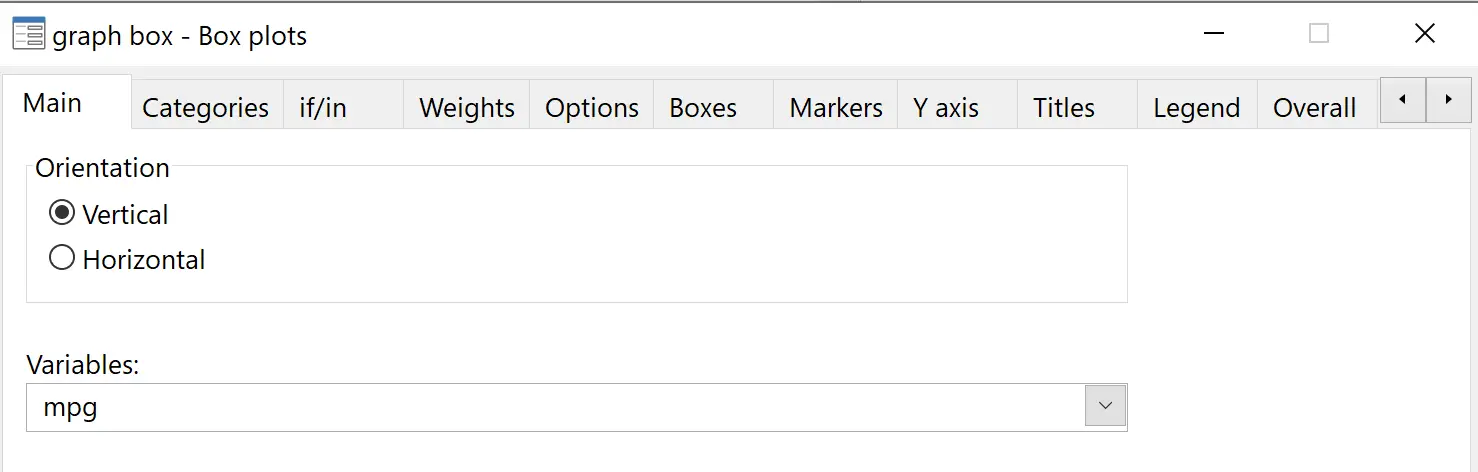
Потім у підзаголовку «Категорії» в розділі «Змінна групування» виберіть «Оброблено» :
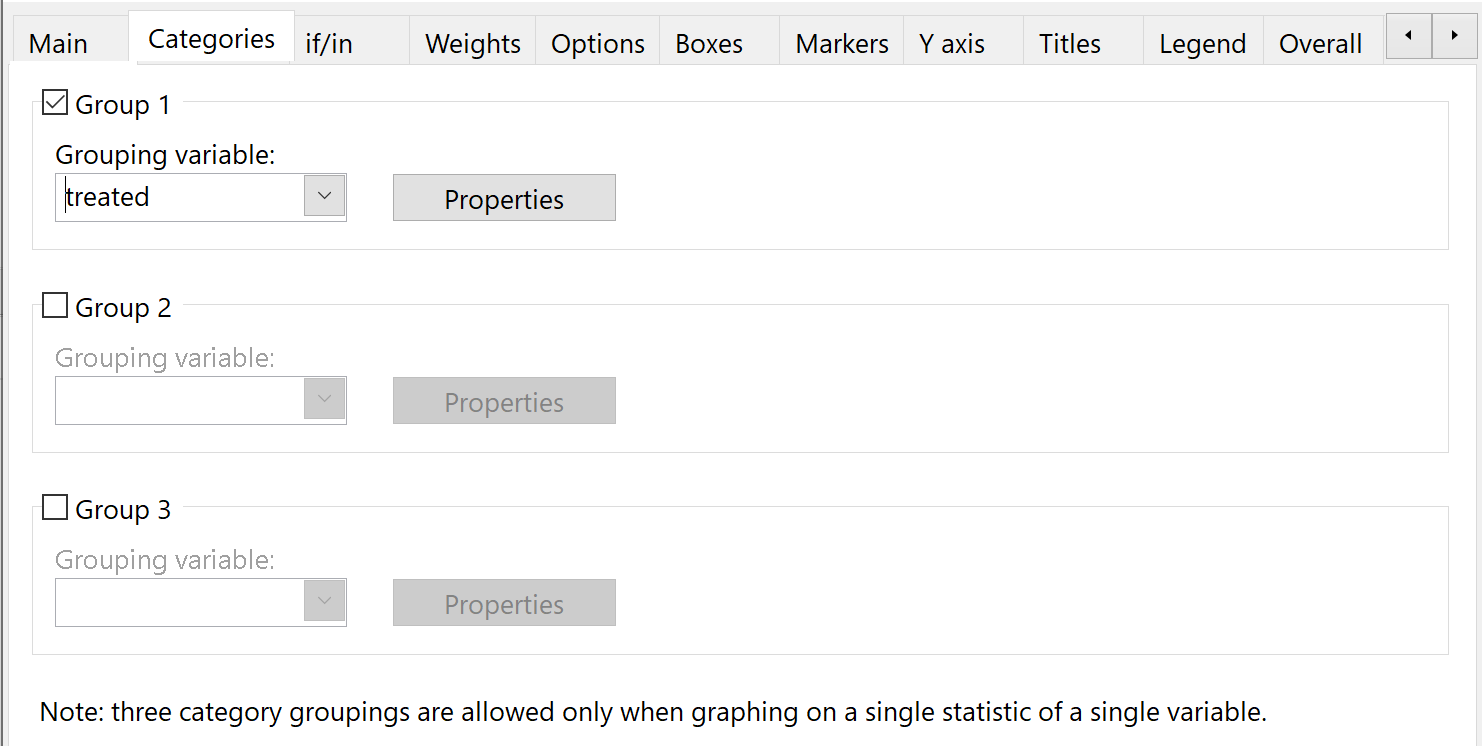
Натисніть OK . Автоматично відобразиться діаграма з двома коробковими графіками:
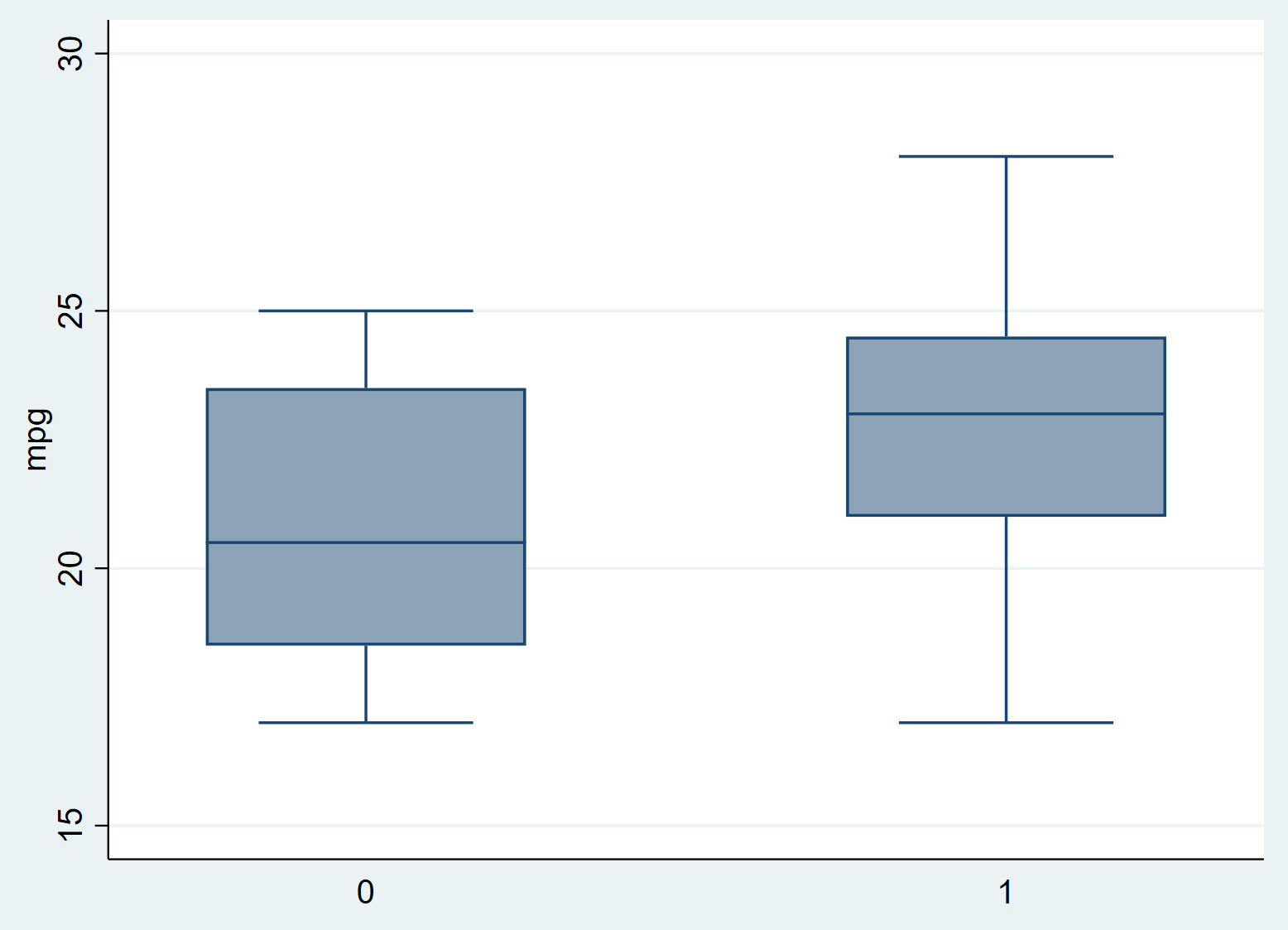
Ми відразу бачимо, що миль на галон виявляється вищим для групи, яка отримувала лікування (1), порівняно з групою, яка не отримувала лікування (0), але нам потрібно виконати t-тест із двома вибірками, щоб побачити, чи є ці відмінності статистично значущими. .
Крок 4: Виконайте двовибірковий t-тест.
У верхній панелі меню перейдіть до Статистика > Підсумки, таблиці та тести > Класичні перевірки гіпотез > t-тест (порівняння середнього рівня) .
Виберіть два зразки за допомогою груп . Для імені змінної виберіть mpg . Для назви змінної групи виберіть Оброблено . Для рівня надійності виберіть потрібний рівень. Значення 95 відповідає рівню значущості 0,05. Ми залишимо це значення 95. Нарешті натисніть OK .
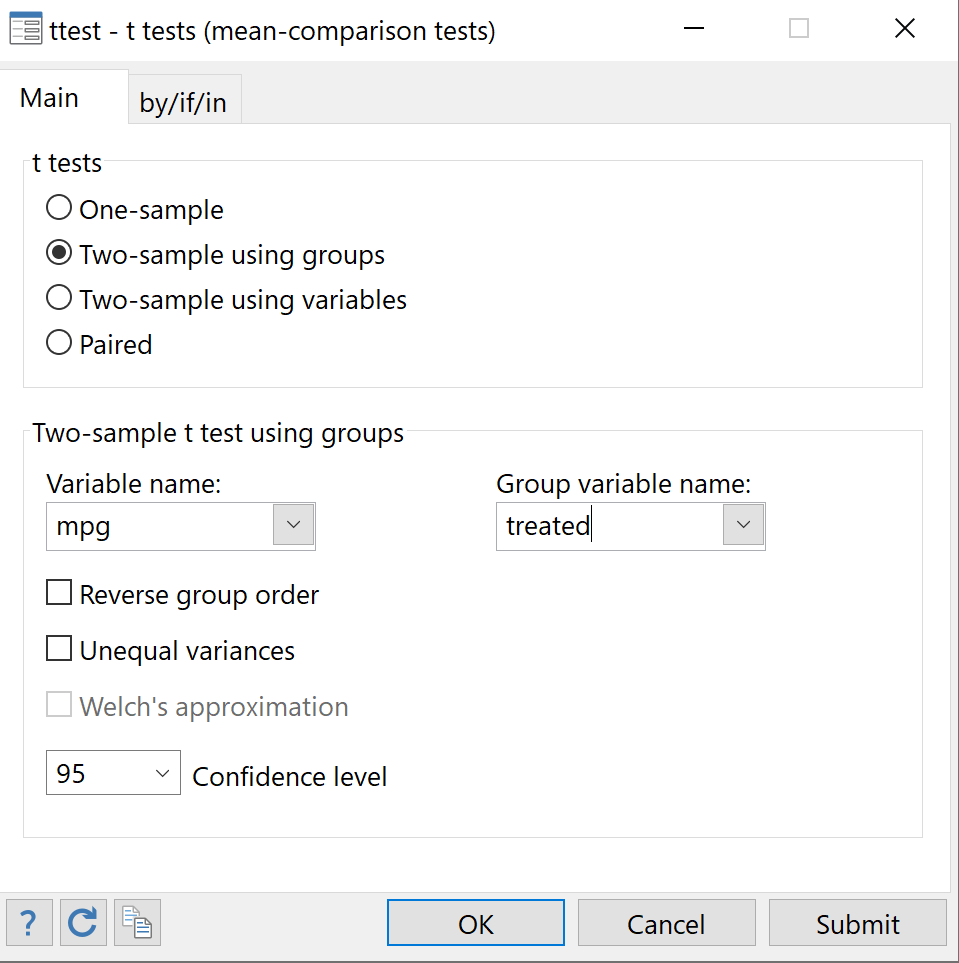
Буде відображено результати двох вибіркових t-тестів:
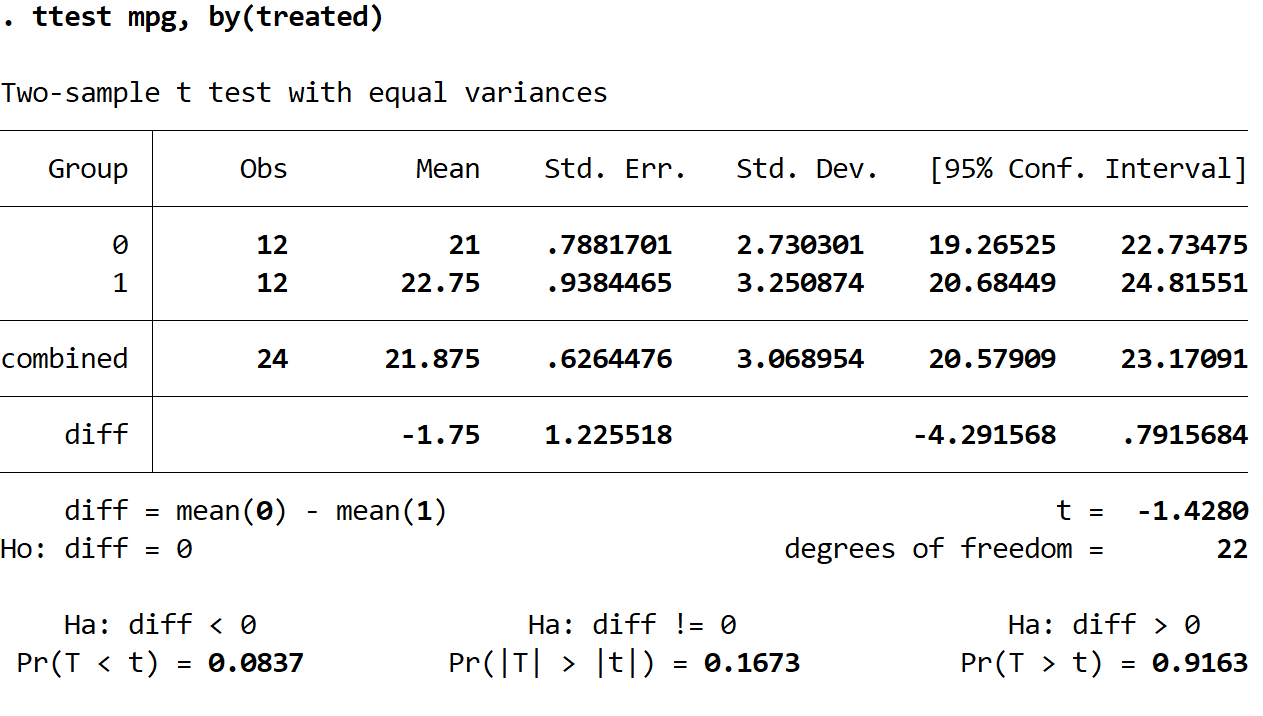
По кожній групі ми отримуємо наступну інформацію:
Obs: кількість спостережень. У кожній групі по 12 спостережень.
Середнє: середнє миль на галлон. У групі 0 середній показник 21. У групі 1 середній показник 22,75.
Стандартний. Err: стандартна помилка, обчислена як σ / √ n
Стандартний. Dev: стандартне відхилення mpg.
95% конф. Діапазон: 95% довірчий інтервал для справжньої середньої кількості населення в милях на галон.
t: тестова статистика двовибіркового t-критерію.
ступені свободи: Ступені свободи для використання для тесту, розраховані як n-2 = 24-2 = 22.
P-значення для трьох різних t-тестів для двох вибірок показано внизу результатів. Оскільки ми хочемо зрозуміти, чи відрізняється середня миля на галон у двох групах, ми розглянемо результати проміжного тесту (в якому альтернативна гіпотеза Ha:diff !=0), який має значення p 0,1673. .
Оскільки це значення не нижче нашого рівня значущості 0,05, ми не можемо відхилити нульову гіпотезу. Ми не маємо достатньо доказів, щоб стверджувати, що справжня середня кількість миль на галон відрізняється між двома групами.
Крок 5: Повідомте про результати.
Нарешті, ми повідомимо результати наших двох вибіркових t-тестів. Ось приклад того, як це зробити:
На 24 автомобілях було проведено T-тест із двома зразками, щоб визначити, чи спричинила нова обробка палива різницю в середніх милях на галон. Кожна група складалася з 12 автомобілів.
Результати показали, що середнє миль на галон не відрізнялося між двома групами (t = -1,428 з df=22, p = 0,1673) на рівні значущості 0,05.
95% довірчий інтервал для справжньої різниці середніх популяцій дав інтервал (-4,29, 0,79).