Як виконати двовибірковий t-тест у excel
Двовибірковий t-критерій використовується, щоб перевірити, чи рівні середні дві сукупності чи ні.
У цьому посібнику пояснюється, як виконати двовибірковий t-тест у Excel.
Як виконати двовибірковий t-тест у Excel
Припустимо, дослідники хочуть знати, чи мають два різні види рослин у певній країні однакову середню висоту. Оскільки вимірювання кожної рослини займе надто багато часу, вони вирішили взяти зразок із 20 рослин кожного виду.
На наступному зображенні показано висоту (у дюймах) кожної рослини в кожному зразку:
Ми можемо виконати двовибірковий t-тест, щоб визначити, чи мають два види однакову середню висоту, виконавши такі дії:
Крок 1: Визначте, чи рівні дисперсії сукупності .
Коли ми виконуємо двовибірковий t-тест, ми повинні спочатку вирішити, чи будемо ми припускати, що дві сукупності мають рівні чи нерівні дисперсії. Загалом можна припустити, що сукупності мають однакові дисперсії, якщо відношення найбільшої дисперсії вибірки до найменшої дисперсії вибірки менше ніж 4:1.
Ми можемо знайти дисперсію для кожного зразка за допомогою функції Excel =VAR.S(Cell range) , як показано на наступному зображенні:
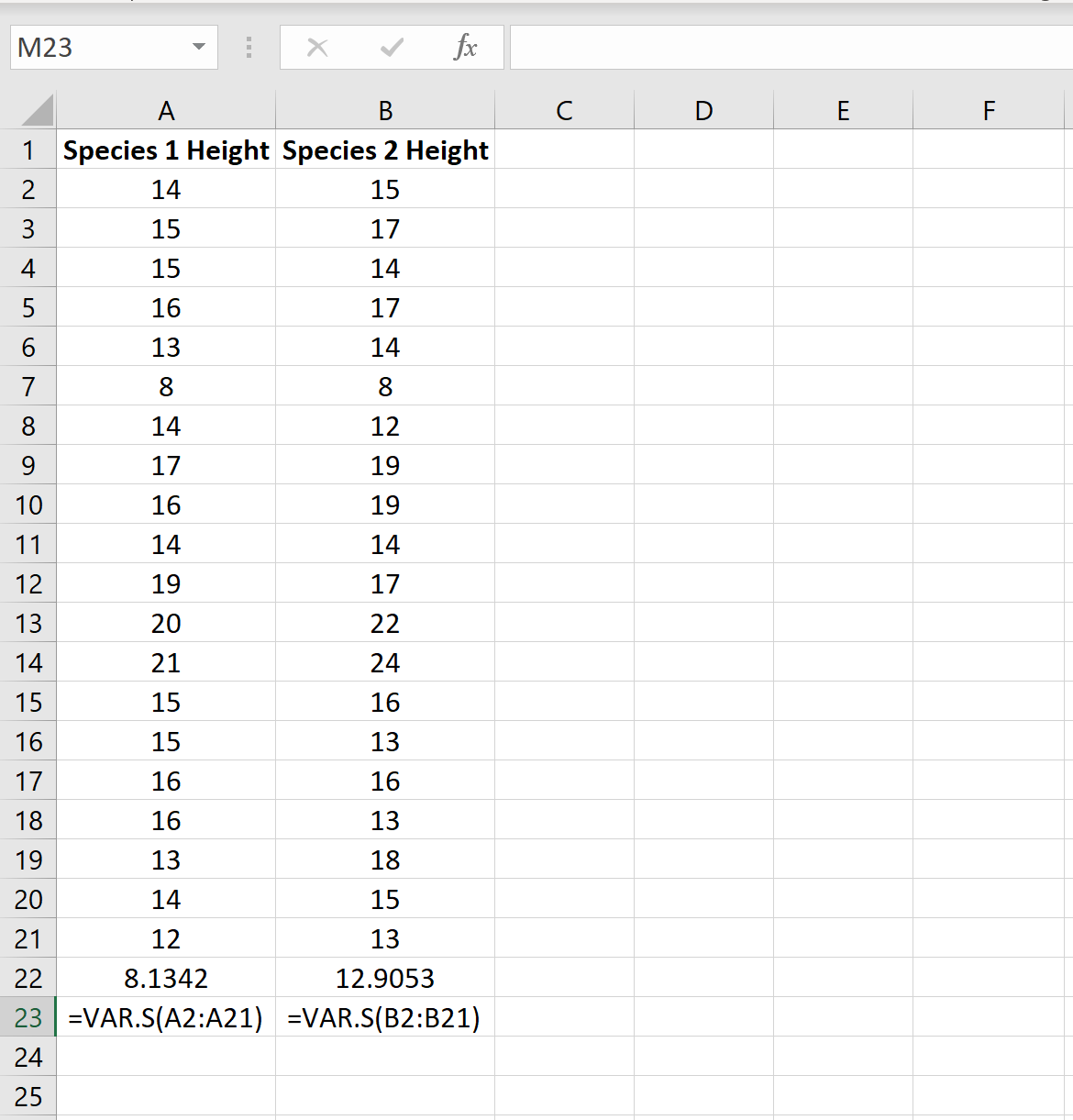
Відношення найбільшої дисперсії вибірки до найменшої дисперсії вибірки становить 12,9053/8,1342 = 1,586 , що менше 4. Це означає, що ми можемо припустити, що дисперсії сукупності рівні.
Крок 2. Відкрийте Analysis ToolPak .
На вкладці «Дані» верхньої стрічки натисніть «Аналіз даних».
Якщо ви не бачите цю опцію, спершу потрібно завантажити Analysis ToolPak , який є абсолютно безкоштовним.
Крок 3: Виберіть відповідний тест для використання.
Виберіть опцію t-критерію: дві вибірки за рівних дисперсій , а потім натисніть OK.
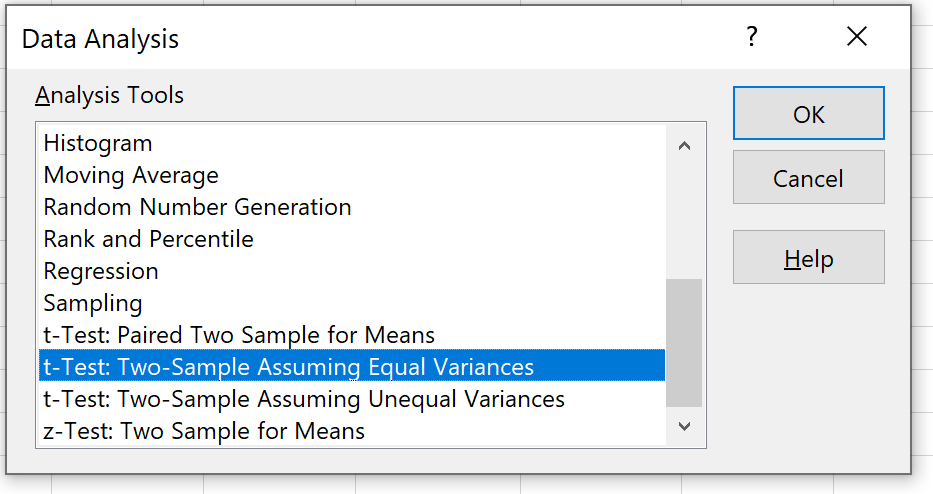
Крок 4: Введіть необхідну інформацію .
Введіть діапазон значень для змінної 1 (наш перший зразок), змінної 2 (наш другий зразок), гіпотетичної середньої різниці (у цьому випадку ми ставимо «0», тому що ми хочемо знати, чи справжня різниця середніх по сукупності дорівнює 0) і вихідний діапазон, у якому ми хотіли б бачити результати t-критерію. Потім натисніть OK.
Крок 5: Інтерпретуйте результати .
Після того, як ви натиснете OK на попередньому кроці, відобразяться результати t-критерію.
Ось як інтерпретувати результати:
Середнє: це середнє значення кожного зразка. Зразок 1 має середню висоту 15,15 , а зразок 2 має середню висоту 15,8 .
Дисперсія: це дисперсія для кожного зразка. Зразок 1 має дисперсію 8,13 , а зразок 2 має дисперсію 12,90 .
Спостереження: це кількість спостережень у кожному зразку. Обидва зразки містять 20 спостережень (наприклад, 20 окремих рослин у кожному зразку).
Об’єднана дисперсія: число, обчислене шляхом «об’єднання» дисперсій кожної вибірки за формулою s 2 p = [ (n 1 -1)s 2 1 + (n 2 -1)s 2 2 ] / (n 1 +n 2 – 2), що виявляється 10,51974 . Потім це число використовується під час обчислення статистики t -критерію.
Гіпотетична різниця середніх: число, про яке ми «висловлюємо гіпотезу», є різницею між середніми двома сукупностями. У цьому випадку ми вибрали 0 , оскільки ми хочемо перевірити, чи дорівнює різниця між середніми двома сукупностями, наприклад, якщо різниці немає.
df: Ступені свободи для t-критерію, розраховані як n 1 + n 2 -2 = 20 + 20 – 2 = 38 .
t Stat: тестова статистика t , обчислена як t = [ x 1 – x 2 ] / √ [s 2 p (1/n 1 + 1/n 2 )]
У цьому випадку t = [15,15-15,8] / √ [10,51974(1/20+1/20)] = -0,63374 .
Двосторонній P(T<=t): p-значення для двобічного t-тесту. У цьому випадку p = 0,530047 . Це набагато більше, ніж альфа = 0,05, тому ми не можемо відхилити нульову гіпотезу. У нас немає достатніх доказів, щоб стверджувати, що засоби двох груп населення різні.
t Двосторонній критичний: це критичне значення тесту, знайдене шляхом ідентифікації значення в таблиці t-розподілу, що відповідає двосторонньому тесту з альфа = 0,05 і df = 38. Це виявляється рівним 2, 024394 . Оскільки наша статистика t- критерію менша за це значення, ми не можемо відхилити нульову гіпотезу. У нас немає достатніх доказів, щоб стверджувати, що засоби двох груп населення різні.
Зауважте, що як підхід p-значення, так і підхід критичного значення приведуть до одного висновку.
Додаткові ресурси
У наступних посібниках пояснюється, як виконувати інші типи t-тестів у Excel:
Як виконати t-критерій однієї вибірки в Excel
Як виконати t-тест парних зразків у Excel
Про автора
Редакція
Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше