Деревоподібна діаграма

У цій статті пояснюється, що таке деревоподібна діаграма та як її створюють. Таким чином, ви знайдете приклади деревоподібних структур, переваги цього типу діаграм і, крім того, крок за кроком розв’язану вправу.

Що таке дерево?

Деревоподібна діаграма , яку також називають деревом ймовірностей , — це графічне представлення всіх можливих результатів експерименту разом із їхніми ймовірностями.

Таким чином, деревоподібна діаграма використовується для побудови всіх можливих результатів у просторі вибірки та обчислення їх ймовірностей.

Деревоподібна діаграма складається таким чином, що кожен результат ( вузол ) розгалужується на нові можливі результати ( гілки ), поки не буде досягнуто кінцевих результатів.

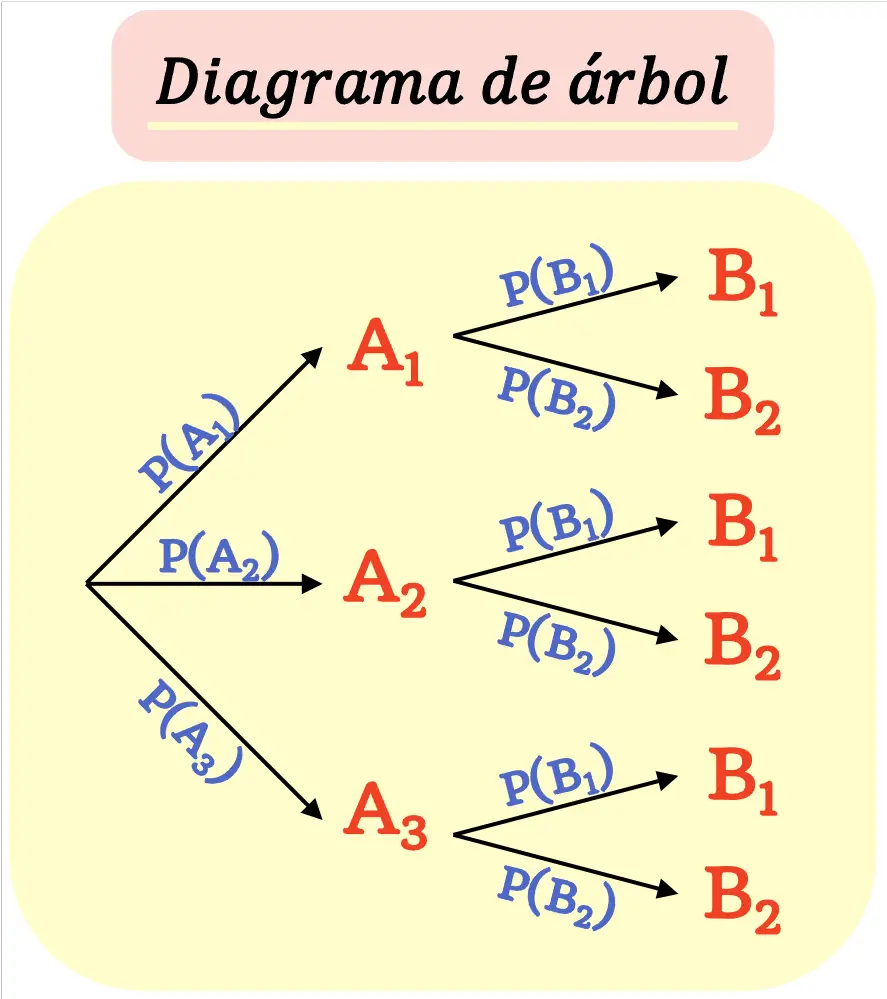
Слід мати на увазі, що сума ймовірностей усіх гілок, що виходять з вузла, повинна дорівнювати 1.

Як зробити схему дерева

Щоб створити дерево, необхідно виконати наступні дії:

1. Першим кроком у створенні деревоподібної діаграми є малювання гілки для кожного можливого результату. Це будуть гілки першого покоління.
2. Потім ймовірність, пов’язана з кожною подією, додається до її відповідної гілки.
3. Кінець кожної гілки першого покоління є вузлом, з якого повинні бути представлені гілки наступних можливих подій.
4. Як і в перших гілках, ми повинні додати ймовірності представлених подій.
5. Повторюйте кроки 3 і 4, доки не досягнете кінцевих вузлів, тобто можливих кінців експерименту.

Зауважте, що кількість гілок на одному рівні не обов’язково має дорівнювати кількості гілок на іншому рівні. Подібним чином кількість розгалужень, які є результатом можливого результату, може змінюватися навіть у межах одного рівня.

Приклад дерева

Тепер, коли ми знаємо визначення та теорію створення деревоподібної діаграми, давайте крок за кроком розглянемо реальний приклад, щоб краще зрозуміти концепцію.

• Побудуйте дерево ймовірностей підкидання трьох незалежних монет. Потім визначте ймовірність отримання голів у всіх трьох підкиданнях.

При жеребкуванні можливі лише два результати, ми можемо отримати орла або решку. Таким чином, ймовірність отримання орла або решки під час підкидання монети становить:

Коли ми знаємо ймовірності можливих результатів, ми переходимо до представлення деревоподібної діаграми.

Оскільки підкидання монет є незалежними, ймовірність отримання орла або решки завжди буде однаковою для кожного підкидання. Тому, щоб побудувати дерево, дві гілки (голова і решка) повинні бути представлені з однаковою ймовірністю для кожного зробленого кидка.

І коли ми зробили дерево, все, що нам потрібно зробити, це визначити ймовірність підкидання трьох монет.

Тому в цьому випадку ми повинні перемножити всі ймовірності отримання голів, тому що це ймовірності шляху, який веде нас до бажаного результату.

Таким чином, ймовірність отримання голів при трьох підкиданнях монети розраховується наступним чином:

Коротше кажучи, ймовірність отримати голови три рази поспіль становить 12,5%.

Розв’язане дерево вправи

У селі є лише 3 ясла: 60% дітей ходять до ясел А, 30% – до ясел Б і 10% – до ясел В. Крім того, у трьох яслах 55% дівчаток. Побудуйте дерево та обчисліть такі ймовірності:

• Імовірність того, що дитина, обрана випадковим чином, буде дівчинкою з дитячого садка B.
• Імовірність того, що дитина випадковим чином буде вибрана з будь-якого дитячого садка, це буде хлопчик.

Зауважте, що якщо частка дівчаток у всіх дитячих садках становить 55%, то відсоток хлопчиків обчислюється простим відніманням 1 мінус 0,55:

Тепер, коли ми знаємо всі ймовірності, ми можемо створити дерево ймовірностей з усіма можливостями:

Таким чином, ймовірність випадкового вибору дівчинки з дитячого садка B обчислюється таким чином:

З іншого боку, щоб визначити ймовірність вибору хлопчика в будь-якому дитячому садку, ми повинні спочатку знайти ймовірність вибору хлопчика для кожного дитячого садка, а потім скласти їх разом:

Переваги деревовидної структури

Завдяки характеристикам деревовидної структури переваги цього типу статистичного графіка такі:

• Деревоподібні діаграми дуже корисні для прийняття рішень.
• Зв’язок між усіма можливими результатами можна зобразити графічно.
• Дуже зручно знайти першопричину проблеми.
• Полегшує розв’язування ймовірнісних і статистичних задач.
• Деревоподібна діаграма допомагає систематизувати ідеї та проаналізувати ситуацію.