Довірчий інтервал для різниці середніх
У цій статті пояснюється, що таке довірчий інтервал для різниці середніх у статистиці та для чого він використовується. Отже, ви дізнаєтесь, як обчислити довірчий інтервал для різниці двох середніх значень, і вправу розв’яжете крок за кроком.
Який довірчий інтервал для різниці середніх?
Довірчий інтервал для різниці середніх – це інтервал, який забезпечує максимальне значення та мінімальне значення, між якими значення різниці середніх двох сукупностей лежить з певним рівнем довіри.
Наприклад, якщо довірчий інтервал для різниці середніх двох генеральних сукупностей з 95% рівнем довіри становить (3,5), це означає, що різниця між середніми двома генеральними сукупностями буде між 3 і 5 з імовірністю 95 %.
Тому в статистиці довірчий інтервал для різниці середніх значень використовується для оцінки двох значень, між якими лежить різниця між двома середніми сукупностями. Таким чином, використовуючи дані з двох вибірок, можна приблизно визначити різницю між середніми сукупностями.
Формула довірчого інтервалу для різниці середніх
Формула для довірчого інтервалу для різниці середніх залежить від того, чи відомі дисперсії генеральної сукупності, і, якщо ні, чи можна вважати дисперсії генеральної сукупності рівними. . Потім ми побачимо, як обчислюється довірчий інтервал для різниці середніх у кожному випадку.
відомі відхилення
Формула для розрахунку довірчого інтервалу для різниці середніх, коли дисперсії двох генеральних сукупностей відомі з рівнем довіри 1-α, виглядає наступним чином:
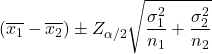
золото:
-

є середнім значенням вибірки i.
-

є стандартним відхиленням сукупності i.
-

– значення стандартного нормального розподілу з імовірністю α/2.
-

це розмір вибірки i.
Цей випадок є найменш поширеним, оскільки значення дисперсій сукупності, як правило, невідоме.
невідомі та рівні дисперсії
Коли дисперсії двох сукупностей невідомі, але їх можна оцінити як рівні, формула для розрахунку довірчого інтервалу для різниці середніх з рівнем довіри 1-α виглядає наступним чином:
![]()
золото:
-

є середнім значенням вибірки i.
-

є зведеним стандартним відхиленням.
-

є значенням t-розподілу Стьюдента n 1 + n 2 -2 ступенів свободи з імовірністю α/2.
-

це розмір вибірки i.
Оскільки в цьому випадку передбачається, що дисперсії генеральної сукупності еквівалентні, комбіноване стандартне відхилення використовується для розрахунку довірчого інтервалу, який обчислюється за такою формулою:

золото
![]()
є стандартним відхиленням вибірки i.
Невідомі та різні варіації
Коли дисперсії двох сукупностей невідомі та не можуть вважатися рівними, формула для розрахунку довірчого інтервалу для різниці середніх з рівнем довіри 1-α виглядає наступним чином:
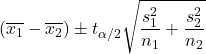
золото:
-

є середнім значенням вибірки i.
-
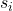
є стандартним відхиленням вибірки i.
-

– значення t-розподілу Стьюдента з імовірністю α/2.
-

це розмір вибірки i.
У цьому випадку ступені вільності t-розподілу Стьюдента розраховуються за такою формулою:

золото
![]()
є стандартним відхиленням вибірки i.
Конкретний приклад довірчого інтервалу для різниці середніх
Ознайомившись із визначенням довірчого інтервалу для різниці середніх і якими є різні формули, тепер ми побачимо конкретний приклад, щоб закінчити засвоєння того, як обчислюється довірчий інтервал для різниці двох середніх.
- Ми хочемо вивчити вплив тютюну на вагу дітей при народженні. Для цього порівнюють дві вибірки: першу складають діти, матері яких не курили, а другу – діти, матері яких курять (параметри вибірки вказані нижче). Обчисліть довірчий інтервал для різниці середніх з довірчим рівнем 95%.
- Матері, які не курять:
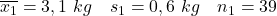
- Матері, що палять:
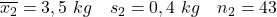
- Матері, які не курять:
У цьому випадку ми не знаємо значень дисперсій сукупності, однак ми можемо припустити, що дисперсії сукупності еквівалентні, оскільки ми маємо справу з двома сукупностями з дуже подібними характеристиками. Отже, формула довірчого інтервалу для різниці середніх, яку ми повинні використовувати, така:
![]()
Таким чином, ми обчислюємо комбіноване стандартне відхилення від стандартних відхилень двох зразків:
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle s_p&=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\\[2ex]\displaystyle s_p&=\sqrt{\frac{(39-1)\cdot 0,6^2+(43-1)\cdot 0,4^2}{39+43-2}}\\[2ex]\displaystyle s_p&=0,50\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-688958252e9838e7fddc2ddcb9061b01_l3.png)
Так само ми повинні знайти значення t-розподілу Стьюдента 80 ступенів свободи з імовірністю 2,5% у таблиці розподілу ймовірностей t-розподілу Стьюдента :
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}t_{\alpha/2| n_1+n_2-2}= \ \color{orange}\bm{?}\\[4ex]t_{0,025|80}=1,990\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-5e4ea90fdc33c9a3d3dab0f1d9d29af0_l3.png)
Нарешті, ми підставляємо дані у формулу довірчого інтервалу для різниці середніх і виконуємо обчислення:
![]()
![]()
![]()
Отже, довірчий інтервал для різниці середніх значень проблеми такий:
![]()