Як створити довірчий інтервал за допомогою f-розподілу

Щоб визначити, чи рівні дисперсії двох сукупностей, ми можемо обчислити відношення дисперсій σ ² ₁ / σ ² ₂ , де σ ² ₁ – це дисперсія сукупності 1, а σ ² ₂ – це дисперсія сукупності 2.

Щоб оцінити справжній коефіцієнт дисперсії генеральної сукупності, ми, як правило, беремо просту випадкову вибірку з кожної генеральної сукупності та обчислюємо співвідношення вибіркової дисперсії, s ₁ ² / s ₂ ² , де s ₁ ² і s ₂ ² є вибірковими дисперсіями для вибірки 1 і вибірки . 2 відповідно.

Цей тест передбачає, що s ₁ ² і s ₂ ² обчислюються з незалежних вибірок розміром n ₁ і n ₂ , обидві з нормально розподілених популяцій.

Чим далі це співвідношення від одиниці, тим сильніші докази нерівних дисперсій у сукупності.

(1-α)100% довірчий інтервал для σ ² ₁ / σ ² ₂ визначається як:

(s ₁ ² / s ₂ ² ) * F _{n 1 -1, n 2 -1, α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (s ₁ ² / s ₂ ² ) * F _{n 2 -1, n 1 -1, α/2}

де F _{n 2 -1, n 1 -1, α/2} і F _{n 1 -1, n 2 -1, α/2}   – критичні значення розподілу F для вибраного рівня значущості α.

Наступні приклади ілюструють, як створити довірчий інтервал для σ ² ₁ / σ ² ₂ за допомогою трьох різних методів:

• За руку
• Використовуйте Microsoft Excel
• Використання статистичного програмного забезпечення R

Для кожного з наступних прикладів ми будемо використовувати таку інформацію:

• α = 0,05
• n ₁ = 16
• _n2 = 11
• s ₁ ² =28,2
• s ₂ ² = 19,3

Створення довірчого інтервалу вручну

Щоб вручну обчислити довірчий інтервал для σ ² ₁ / σ ² ₂ , ми просто підставимо отримані числа у формулу довірчого інтервалу:

(s ₁ ² / s ₂ ² ) * F _{n1-1, n2-1,α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (s ₁ ² / s ₂ ² ) * F _{n2-1, n1-1, α/2}

Єдині цифри, яких нам не вистачає, це критичні значення. На щастя, ми можемо знайти ці критичні значення в таблиці розподілу F :

F _{n2-1, n1-1, α/2} = F _{10, 15, 0,025} = 3,0602

F _{n1-1, n2-1, α/2} = 1/ F _{15, 10, 0,025} = 1 / 3,5217 = 0,2839

(Натисніть, щоб збільшити таблицю)

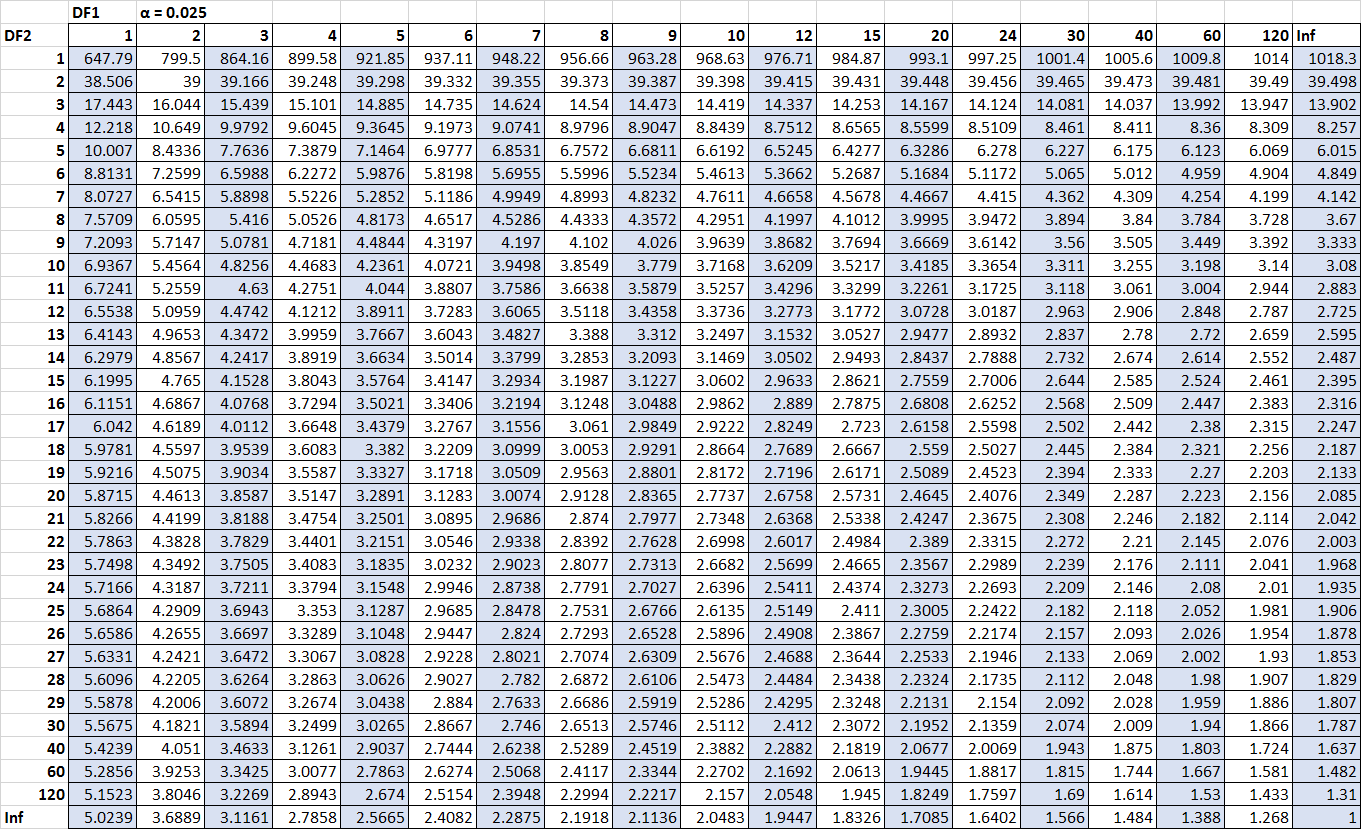
Тепер ми можемо підставити всі числа до інтервалу формули довіри:

(s ₁ ² / s ₂ ² ) * F _{n1-1, n2-1,α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (s ₁ ² / s ₂ ² ) * F _{n2-1, n1-1, α/2}

(28,2 / 19,3) * (0,2839) ≤ σ ² ₁ / σ ² ₂ ≤ (28,2 / 19,3) * (3,0602)

0,4148 ≤ σ ² ₁ / σ ² ₂ ≤ 4,4714

Таким чином, 95% довірчий інтервал для співвідношення дисперсій сукупності становить (0,4148, 4,4714) .

Створення довірчого інтервалу за допомогою Excel

На наступному зображенні показано, як обчислити 95% довірчий інтервал для коефіцієнта дисперсії сукупності в Excel. Нижня та верхня межі довірчого інтервалу показані в стовпці E, а формула, яка використовується для визначення нижньої та верхньої меж, показана в стовпці F:

Таким чином, 95% довірчий інтервал для співвідношення дисперсій сукупності становить (0,4148, 4,4714) . Це відповідає тому, що ми отримали, коли вручну обчислили довірчий інтервал.

Створення довірчого інтервалу за допомогою R

Наступний код ілюструє, як обчислити 95% довірчий інтервал для співвідношення дисперсій сукупності в R:

 #define significance level, sample sizes, and sample variances
alpha <- .05
n1 <- 16
n2 <- 11
var1 <- 28.2
var2 <- 19.3

#define F critical values
upper_crit <- 1/qf(alpha/2, n1-1, n2-1)
lower_crit <- qf(alpha/2, n2-1, n1-1)

#find confidence interval
lower_bound <- (var1/var2) * lower_crit
upper_bound <- (var1/var2) * upper_crit

#output confidence interval
paste0("(", lower_bound, ", ", upper_bound, " )")

#[1] "(0.414899337980266, 4.47137571035219 )"

Таким чином, 95% довірчий інтервал для співвідношення дисперсій сукупності становить (0,4148, 4,4714) . Це відповідає тому, що ми отримали, коли вручну обчислили довірчий інтервал.

Додаткові ресурси

Як читати F розподільний щит
Як знайти критичне значення F в Excel