Експериментальна ймовірність

Тут ви знайдете значення експериментальної ймовірності та спосіб обчислення експериментальної ймовірності. Крім того, ви зможете побачити покроковий приклад розрахунку експериментальної ймовірності.

Що таке експериментальна ймовірність?

Експериментальна ймовірність — це статистичний показник, заснований на результатах експерименту або емпіричних фактах і вказує на ймовірність настання події.

Крім того, чим частіше експеримент повторюється, тим точнішою буде отримана експериментальна ймовірність. З цієї причини комп’ютерні програми, здатні швидко симулювати тисячі експериментів, як правило, використовуються для визначення експериментальної ймовірності, отже отримуючи кращу точність.

Експериментальна ймовірність також відома як емпірична ймовірність або частотна ймовірність .

Експериментальна ймовірність — це число від 0 до 1. Логічно, чим більше значення експериментальної ймовірності події, тим більша ймовірність її настання, і навпаки, чим менше значення, тим менша ймовірність її настання. може статися. або відбувається подія. Але значення експериментальної ймовірності завжди буде між нулем і одиницею.

Формула експериментальної ймовірності

Формула експериментальної ймовірності — це кількість разів, коли подія сталася під час експерименту, поділена на загальну кількість разів, коли експеримент проводився.

Наприклад, якщо людина кидає десять дротиків у мішень і встигає влучити в 6 дротиків у центрі, ймовірність того, що ця людина влучить у мішень у центрі, обчислюється наступним чином:

Приклад експериментальної ймовірності

Коли ми побачимо математичне визначення експериментальної ймовірності, ми розв’яжемо покрокову вправу на цей тип ймовірності. Мета полягає в тому, щоб ви дізналися, як розраховується експериментальна ймовірність події, тому, якщо у вас є запитання, ви можете писати їх у коментарях.

• Обчисліть експериментальну ймовірність елементарних подій, які складають випадковий експеримент підкидання кубика.

Перш ніж знайти експериментальну ймовірність, ми розрахуємо теоретичну ймовірність, щоб порівняти отримані експериментальні результати з теоретичними. Як ви добре знаєте, під час кидання кубика існує шість можливих результатів (1, 2, 3, 4, 5 і 6), тому теоретична ймовірність кожної елементарної події дорівнює:

Щоб розв’язати цю вправу, ми повинні імітувати кидання кубика кілька разів і записати результати в таблицю непередбачуваності. У цьому випадку ми будемо виконувати моделювання за допомогою програми Excel, але ви, очевидно, можете використовувати програму на свій вибір.

Спочатку ми змоделюємо десять кидків, потім сто кидків і, нарешті, тисячу кидків. Таким чином ми зможемо проаналізувати результати та побачити, як вони змінюються залежно від розміру вибірки експерименту. Результати, отримані після випадкового моделювання 10 кидків кубиків, такі:

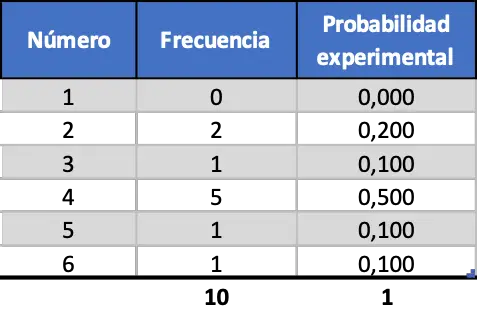
Як бачите, отримані експериментальні ймовірності наразі сильно відрізняються від теоретичних ймовірностей, розрахованих раніше (0,167).

Але в міру того, як ми збільшуємо кількість тестів, ці два показники стають більш схожими, подивіться на симуляцію 100 запусків:

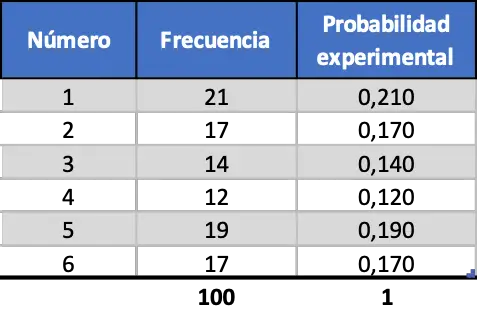
Тепер експериментальна ймовірність виглядає більше як теоретичне значення ймовірності, однак ми все ще отримуємо далекі значення.

Нарешті, ми виконуємо ту саму процедуру, але симулюємо 1000 запусків:

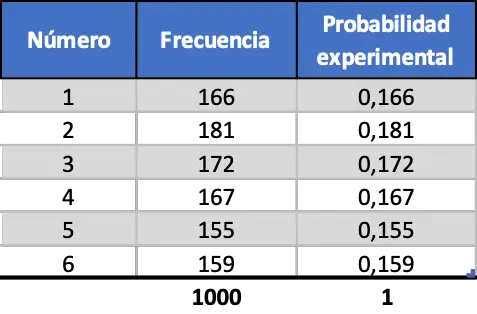
Як ви можете бачити в останній таблиці непередбачуваності, тепер значення експериментальних ймовірностей дуже схожі на теоретичні ймовірності.

Таким чином, чим більша кількість проведених експериментів, тим ближче значення експериментальної ймовірності події буде до її теоретичної ймовірності . Це правило визначається як закон великих чисел , який стверджує, що чим більше даних, тим ближчими експериментальні значення будуть до теоретичних.

Подібним чином, якщо ви порівняєте три частотні таблиці, ви побачите, що експериментальна ймовірність не є остаточною, але що вона змінюється залежно від кількості проведених експериментів. Це означає, що ви повинні знати, як інтерпретувати отримані значення.

Експериментальна ймовірність і теоретична ймовірність

Різниця між експериментальною ймовірністю та теоретичною ймовірністю (або класичною ймовірністю) полягає в тому, що експериментальна ймовірність обчислюється на основі даних, зібраних під час реального експерименту, тоді як теоретична ймовірність обчислюється без необхідності проведення будь-якого експерименту.

Як ми бачили, ми повинні змоделювати велику кількість експериментів, щоб визначити експериментальну ймовірність події. Однак обчислення теоретичної ймовірності пов’язане з теорією та логікою. Ви можете побачити, як це робиться тут: