Вступ до експоненціального розподілу

Експоненціальний розподіл — це розподіл ймовірностей, який використовується для моделювання часу, який ми маємо чекати, поки не станеться певна подія.

Цей розподіл можна використовувати для відповіді на такі питання, як:

• Як довго роздрібний продавець повинен чекати, поки клієнт увійде до його магазину?
• Як довго ноутбук працюватиме, перш ніж він зламається?
• Як довго автомобільний акумулятор працюватиме, перш ніж розрядиться?
• Як довго нам чекати наступного виверження вулкана в певному регіоні?

У кожному сценарії ми хочемо підрахувати, скільки часу нам доведеться чекати, поки відбудеться певна подія. Таким чином, кожен сценарій може бути змодельований за допомогою експоненціального розподілу.

Експоненціальний розподіл: PDF і CDF

Якщо випадкова величина X має експоненціальний розподіл, то функцію щільності ймовірності X можна записати:

f (x; λ) = λe ^-λx

золото:

• λ: параметр швидкості (розраховується як λ = 1/μ)
• e: константа, яка приблизно дорівнює 2,718

Кумулятивна функція розподілу

F (x; λ) = 1 – e ^-λx

На практиці CDF найчастіше використовується для обчислення ймовірностей, пов’язаних з експоненціальним розподілом.

Наприклад, припустимо, що середня кількість хвилин між виверженнями певного гейзера становить 40 хвилин. Наскільки ймовірно, що виверження доведеться чекати менше 50 хвилин?

Щоб вирішити цю задачу, нам спочатку потрібно обчислити параметр швидкості:

• λ = 1/мк
• λ = 1/40
• λ = 0,025

Ми можемо підставити λ = 0,025 і x = 50 у формулу CDF:

• P(X ≤ x) = 1 – e ^-λx
• P(X ≤ 50) = 1 – e ^-0,025(50)
• P(X ≤ 50) = 0,7135

Імовірність того, що наступного виверження доведеться чекати менше 50 хвилин, становить 0,7135 .

Візуалізуйте експоненціальний розподіл

На наступному графіку показано функцію щільності ймовірності випадкової величини

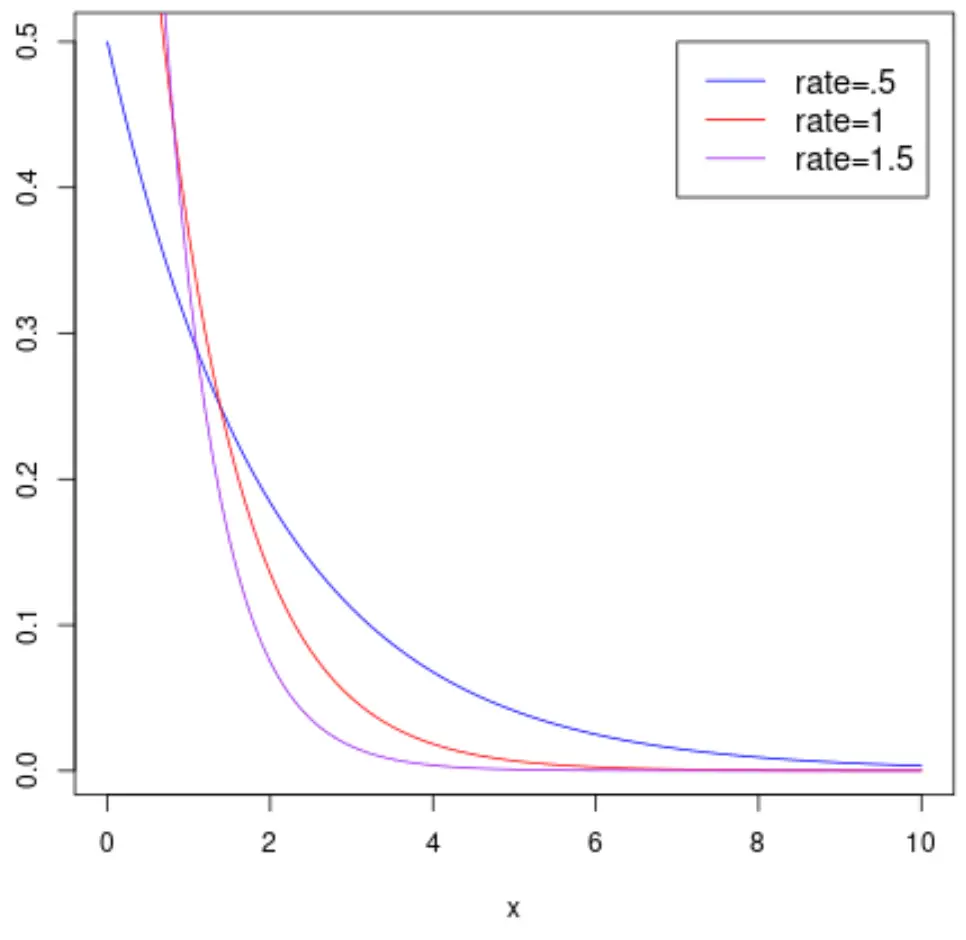
На наступному графіку показано кумулятивну функцію розподілу випадкової величини X , яка відповідає експоненціальному розподілу з різними параметрами швидкості:

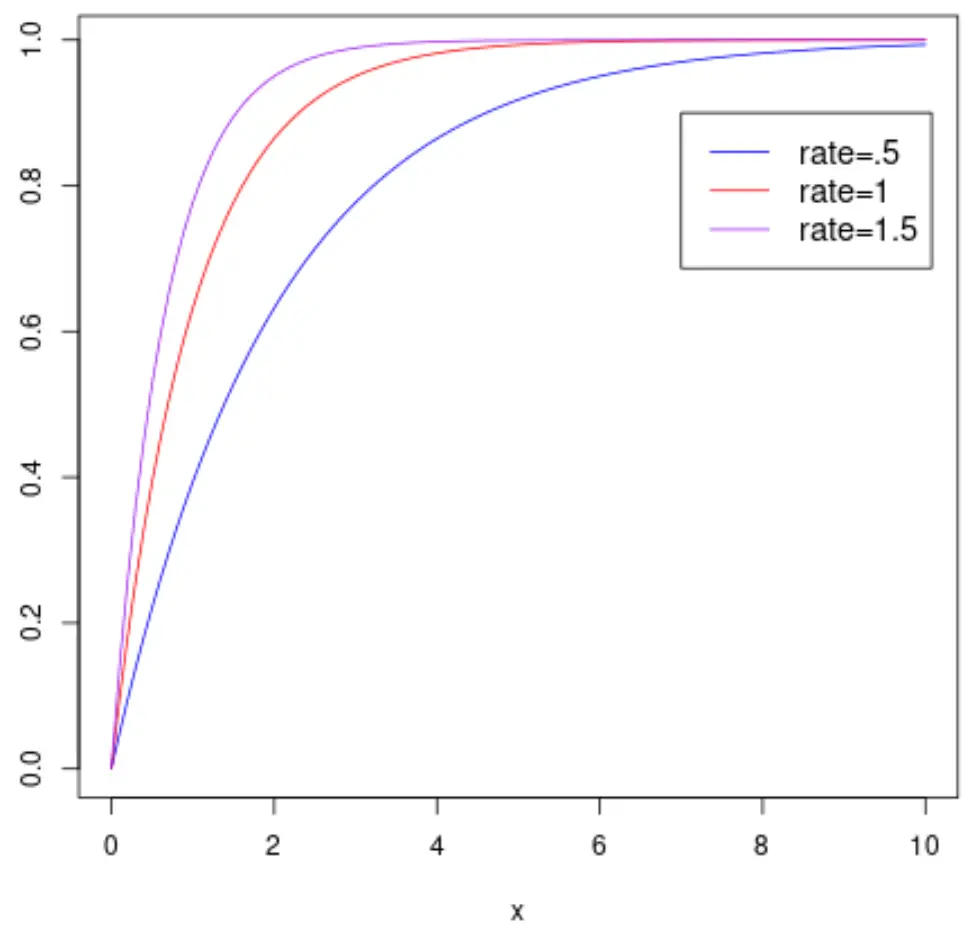
Примітка. Перегляньте цей підручник , щоб дізнатися, як побудувати графік експоненціального розподілу в R.

Властивості експоненціального розподілу

Експоненціальний розподіл має такі властивості:

• Середнє: 1 / λ
• Різниця: 1 / λ ²

Наприклад, припустимо, що середня кількість хвилин між виверженнями певного гейзера становить 40 хвилин. Ми розрахуємо швидкість як λ = 1/μ = 1/40 = 0,025.

Тоді ми могли б обчислити такі властивості для цього розподілу:

• Середній час очікування наступного виверження: 1/λ = 1 /,025 = 40
• Різниця в часі очікування наступного виверження: 1/λ ² = 1 /,025 ² = 1600

Примітка. Експоненціальний розподіл також має властивість безпам’яті , що означає, що на ймовірність майбутньої події не впливає настання минулих подій.

Практичні задачі експоненціального розподілу

Використовуйте наведені нижче практичні завдання, щоб перевірити свої знання про експоненціальний розподіл.

Питання 1: Новий клієнт заходить до магазину в середньому кожні дві хвилини. Після прибуття клієнта визначте ймовірність того, що новий клієнт прийде менш ніж за хвилину.

Рішення 1. Середній час між клієнтами становить дві хвилини. Таким чином, ставку можна розрахувати наступним чином:

• λ = 1/мк
• λ = 1/2
• λ = 0,5

Ми можемо підставити λ = 0,5 і x = 1 у формулу CDF:

• P(X ≤ x) = 1 – e ^-λx
• P(X ≤ 1) = 1 – e ^-0,5(1)
• P(X ≤ 1) = 0,3935

Імовірність того, що нам доведеться чекати менше хвилини на прибуття наступного клієнта, становить 0,3935 .

Запитання 2: Землетрус відбувається в середньому кожні 400 днів у певному регіоні. Після землетрусу визначте ймовірність того, що до наступного землетрусу пройде понад 500 днів.

Рішення 2: Середній час між землетрусами становить 400 днів. Таким чином, ставку можна розрахувати наступним чином:

• λ = 1/мк
• λ = 1/400
• λ = 0,0025

Ми можемо підключити λ = 0,0025 і x = 500 до формули CDF:

• P(X ≤ x) = 1 – e ^-λx
• P(X ≤ 1) = 1 – e ^-0,0025(500)
• P(X ≤ 1) = 0,7135

Імовірність того, що наступного землетрусу доведеться чекати менше 500 днів, становить 0,7135. Таким чином, ймовірність того, що наступного землетрусу нам доведеться чекати понад 500 днів, становить 1 – 0,7135 = 0,2865 .

Запитання 3: Кол-центр отримує новий дзвінок в середньому кожні 10 хвилин. Після дзвінка клієнта визначте ймовірність того, що новий клієнт подзвонить протягом 10-15 хвилин.

Рішення 3: середній час між дзвінками становить 10 хвилин. Таким чином, ставку можна розрахувати наступним чином:

• λ = 1/мк
• λ = 1/10
• λ = 0,1

Для розрахунку ймовірності того, що новий клієнт зателефонує протягом 10-15 хвилин, ми можемо використовувати таку формулу:

• P(10 < X ≤ 15) = (1 – e ^-0,1(15) ) – (1 – e ^-0,1(10) )
• P(10 < X ≤ 15) = 0,7769 – 0,6321
• P(10 < X ≤ 15) = 0,1448

Імовірність того, що новий клієнт подзвонить протягом 10-15 хвилин. дорівнює 0,1448 .

Додаткові ресурси

Наступні навчальні посібники містять вступ до інших поширених розподілів ймовірностей.

Введення в нормальний розподіл
Введення в біноміальний розподіл
Введення в розподіл Пуассона
Вступ до рівномірного розподілу