Експоненціальний розподіл

за Редакція 3 Серпня, 2023 Ймовірність 0 коментарів

У цій статті пояснюється, що таке експоненціальний розподіл у статистиці та для чого він використовується. Так само ви знайдете властивості експоненціального розподілу, а також його формули, графік і розв’язану вправу. Крім того, ви зможете розрахувати будь-яку ймовірність за допомогою онлайн-калькулятора експоненціального розподілу.

Що таке експоненціальний розподіл?

Експоненціальний розподіл — це безперервний розподіл ймовірностей, який використовується для моделювання часу очікування виникнення випадкового явища.

Точніше, експоненціальний розподіл дозволяє нам описати час очікування між двома подіями, який відповідає розподілу Пуассона. Тому експоненціальний розподіл тісно пов’язаний з розподілом Пуассона.

➤ Дивіться: Що таке розподіл Пуассона?

Експоненціальний розподіл має характерний параметр, представлений грецькою літерою λ, і вказує кількість разів, коли досліджувана подія має відбутися протягом певного періоду часу.

$X\sim \text{Exp}(\lambda)$

Подібним чином, експоненціальний розподіл також використовується для моделювання часу до появи збою. Отже, експоненціальний розподіл має декілька застосувань у теорії надійності та виживання.

Приклади експоненціальних розподілів

Тепер, коли ми знаємо визначення експоненціального розподілу, давайте розглянемо кілька прикладів цього типу розподілу, щоб краще зрозуміти концепцію.

Приклади експоненціального розподілу:

Час, що минув між двома дзвінками в кол-центрі.
Час, який людина повинна чекати, поки по конкретній вулиці проїде вільне таксі.
Час очікування до входу нового клієнта в магазин.
Час, який проходить між двома різними користувачами, які заходять на веб-сторінку.
Час, що минув в аеропорту між зльотом одного літака та вильотом іншого.

Формула експоненціального розподілу

Формула функції щільності, яка визначає обчислення ймовірності експоненціального розподілу, дорівнює λ, помноженому на число e у степені від’ємного λ, помноженого на x.

Іншими словами, формула для обчислення ймовірності експоненціального розподілу виглядає наступним чином:

👉 Ви можете скористатися наведеним нижче калькулятором, щоб обчислити ймовірність змінної, яка відповідає експоненціальному розподілу.

З іншого боку, формула для обчислення кумулятивної ймовірності експоненціального розподілу така:

$P[X\leq x]=1-e^{-\lambda x}$

Графік експоненціального розподілу

У цьому розділі ви можете побачити графічне представлення функції густини та функції розподілу експоненціального розподілу.

Нижче можна побачити, як змінюється графік функції щільності експоненціального розподілу в залежності від значення параметра λ.

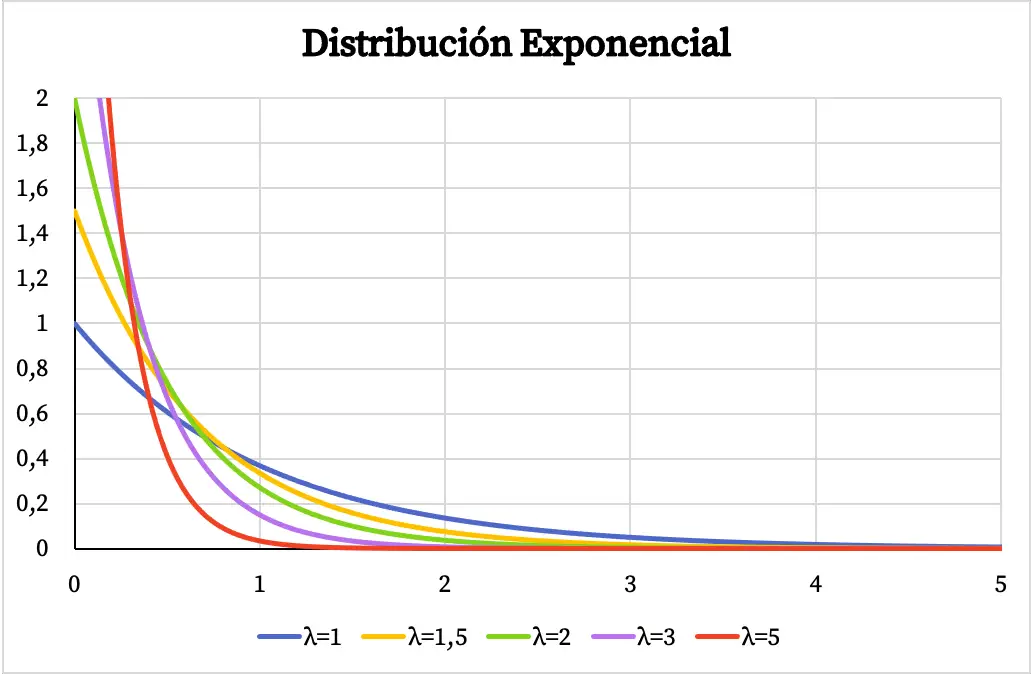
Подібним чином кумулятивна функція ймовірності експоненціального розподілу також залежить від значення параметра λ, як ви можете бачити на наступному графіку:

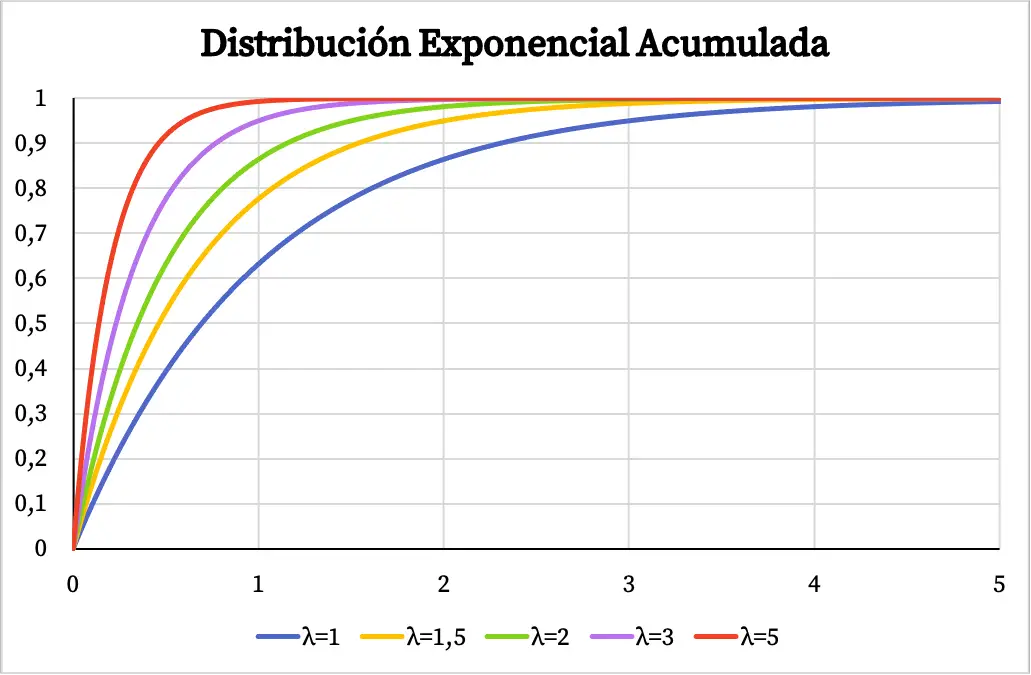
графік імовірності експоненціального кумулятивного розподілу

Розв’язана вправа на експоненціальний розподіл

У середньому λ=1 користувач/хв отримує доступ до певної веб-сторінки. Яка ймовірність того, що час між входом двох користувачів становить 3 хвилини? А ймовірність того, що він дорівнює або менше 2 хвилин?

Розподіл, який визначає випадкову величину цієї задачі, є експоненціальним розподілом, оскільки ми вивчаємо час, який проходить від моменту події (входу користувача на веб-сторінку) до повторного повторення цієї самої події.

$X\sim \text{Exp}(1)$

Тому, щоб обчислити ймовірність того, що час, що минув між входом двох різних користувачів, становить три хвилини, нам потрібно застосувати формулу функції щільності (див. вище):

$\begin{aligned}P[X=x]&=\lambda e^{-\lambda x}\\[2ex]P[X=3]&=1\cdot e^{-1\cdot 3}\\[2ex]P[X=3]&=0,05\end{aligned}$

З іншого боку, щоб визначити кумулятивну ймовірність, ми повинні використовувати формулу функції розподілу експоненціального розподілу:

$\begin{aligned}P[X\leq x]&=1- e^{-\lambda x}\\[2ex]P[X\leq 2]&=1-e^{-1\cdot 2}\\[2ex]P[X\leq 2]&=0,86\end{aligned}$

Характеристики експоненціального розподілу

Експоненціальний розподіл має такі характеристики:

Експоненціальний розподіл має характерний параметр λ, який вказує кількість разів, коли досліджуване явище має виникнути протягом певного періоду часу.

$X\sim \text{Exp}(\lambda)$

Експоненціальний розподіл не може мати від’ємного значення, тому область експоненціального розподілу складається з усіх дійсних чисел, більших або рівних нулю.

$x\in [0,+\infty)$

Середнє значення експоненціального розподілу дорівнює одиниці, поділеній на характерний параметр λ.

$E[X]=\cfrac{1}{\lambda}$

Дисперсія експоненціального розподілу є квадратом його середнього, тому дисперсія експоненціального розподілу еквівалентна одиниці за квадратом коефіцієнта λ.

$Var(X)=\cfrac{1}{\lambda^2 }$

Яким би не було значення λ, коефіцієнт асиметрії експоненціального розподілу завжди дорівнює 2.

$A=2$

Подібним чином, коефіцієнт ексцесу будь-якого експоненціального розподілу завжди дорівнює 9.

$C=9$

Формула для функції щільності експоненціального розподілу:

$P[X=x]=\lambda e^{-\lambda x}$

Тоді як формула для кумулятивної функції ймовірності експоненціального розподілу виглядає наступним чином:

$P[X\leq x]=1-e^{-\lambda x}$

Експоненціальний розподіл є одним із небагатьох розподілів ймовірностей із властивістю браку пам’яті. Ця властивість означає, що поява попередньої події не впливає на ймовірність того, що ця подія відбудеться в майбутньому. Наприклад, у експоненціальному розподілі ймовірність того, що новий користувач отримає доступ до веб-сторінки менш ніж за хвилину, не залежить від того, чи користувач щойно увійшов, чи ніхто з тих пір не входив. більше десяти хвилин.

$P[X>x+y|X>y]=P[X>x]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”254″ style=”vertical-align: -5px;”></p> </p> <h2 class=$ Калькулятор експоненціального розподілу

Введіть значення параметра λ і значення x у наступний калькулятор, щоб обчислити ймовірність. Вам потрібно вибрати ймовірність, яку ви хочете обчислити, і введіть числа, використовуючи крапку як десятковий роздільник, наприклад 0,50.

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше