Емпірична ймовірність
У цій статті ми пояснюємо, як обчислити емпіричну ймовірність. Ви дізнаєтеся, що таке емпірична ймовірність, яка її формула, приклад і чим емпірична ймовірність відрізняється від теоретичної.
Що таке емпірична ймовірність?
Емпірична ймовірність — це статистичний показник, заснований на емпіричних експериментах або фактах, який вказує на ймовірність події.
Іншими словами, емпірична ймовірність розраховується за результатами експерименту та повідомляє нам, наскільки ймовірна подія.
Чим частіше експеримент повторюється, тим точнішою буде отримана емпірична ймовірність. Ось чому цей тип ймовірності зазвичай визначається за допомогою комп’ютерних програм, які моделюють тисячі ітерацій і здатні аналізувати їх за дуже короткий час.
Емпірична ймовірність — це число від 0 до 1. Чим більша ймовірність події, тим вища емпірична ймовірність, і навпаки, чим менша ймовірність події, тим менша її емпірична ймовірність.
Формула емпіричної ймовірності
Формула емпіричної ймовірності — це кількість разів, коли подія сталася під час експерименту, поділена на загальну кількість разів, коли експеримент проводився.
![]()
Наприклад, якщо ми дивимося на дерево десять разів і ми бачили птаха на дереві сім разів, емпірична ймовірність побачити птаха, дивлячись на дерево, буде:
![]()
Приклад емпіричної ймовірності
Розглядаючи визначення емпіричної ймовірності, розв’яжемо покрокову вправу на цей тип ймовірності. Таким чином ви можете побачити, як розраховується емпірична ймовірність.
- Обчислює емпіричну ймовірність елементарних подій, які складають випадковий експеримент із киданням кубика.
Спочатку розрахуємо теоретичну ймовірність порівняння отриманих експериментальних результатів з теоретичними. Існує шість можливих результатів під час кидання кубика (1, 2, 3, 4, 5 і 6), тому теоретична ймовірність кожної елементарної події дорівнює:
![]()
Щоб розв’язати цю вправу, ми повинні імітувати кидання кубика кілька разів і записати результати в таблицю непередбачуваності. Для цього ми можемо використати, наприклад, програму Excel.
Щоб ви могли зрозуміти важливість кількості проведених експериментів, ми спочатку змоделюємо десять запусків, потім сто і, нарешті, тисячу. Таким чином, результати, отримані в результаті моделювання перших 10 випадкових кидків кубика, такі:
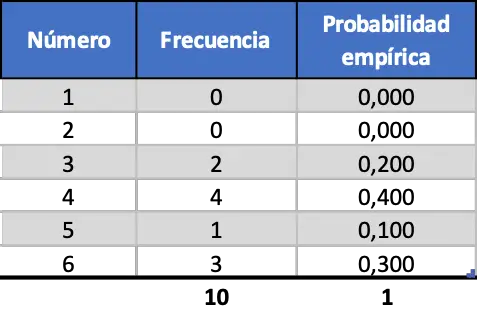
Як бачимо, емпіричні ймовірності, отримані шляхом моделювання лише десяти кидків, не близькі до теоретичних ймовірностей (0,167).
Але коли ми збільшуємо кількість експериментів, ці два показники стають більш схожими, подивіться на симуляцію 100 запусків:
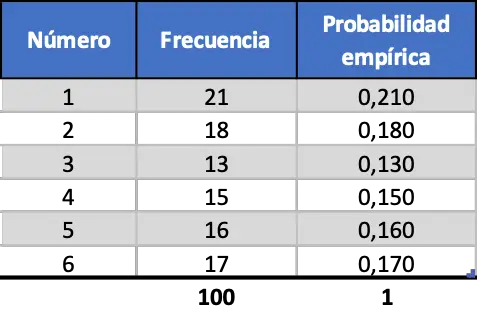
Тепер емпірична ймовірність, розрахована для кожного числа на кубику, більше схожа на теоретичну ймовірність, однак ми все ще отримуємо дуже різні значення.
Нарешті, ми виконуємо ту саму процедуру, але симулюємо 1000 запусків:
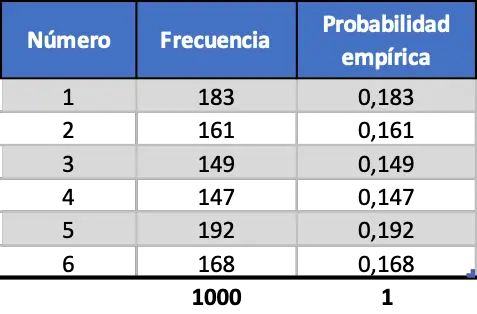
Як ми бачимо в останній таблиці непередбачуваності, тепер значення емпіричних ймовірностей дуже близькі до теоретичних.
Підводячи підсумок, чим більше ми збільшуємо кількість проведених експериментів, тим ближчим буде значення емпіричної ймовірності події до її теоретичної ймовірності виникнення . Це правило визначається як закон великих чисел , який стверджує, що чим більше даних, тим ближчими експериментальні значення будуть до теоретичних.
Крім того, якщо порівняти три частотні таблиці, ми побачимо, що емпірична ймовірність не є остаточною, але вона змінюється залежно від кількості проведених експериментів. Це означає, що ви повинні знати, як інтерпретувати отримані значення.
Емпірична ймовірність і теоретична ймовірність
Нарешті, ми проаналізуємо поняття емпіричної ймовірності та поняття теоретичної ймовірності, тому що, хоча це два типи ймовірностей, вони мають абсолютно різне значення.
Різниця між емпіричною ймовірністю та теоретичною ймовірністю (або класичною ймовірністю) полягає в тому, що емпірична ймовірність обчислюється на основі даних, зібраних із реального досвіду, тоді як теоретична ймовірність обчислюється з урахуванням ідеальних обставин без проведення будь-яких експериментів.
Тобто, щоб знайти емпіричну ймовірність, необхідно змоделювати експеримент і провести розрахунок на основі отриманих результатів. Але щоб дізнатися теоретичну ймовірність, не потрібно проводити експеримент, а лише теоретичний розрахунок.
Крім того, рівень зміщення визначається як різниця між емпіричною ймовірністю та теоретичною ймовірністю. Зміщення може бути позитивним або негативним, але дуже важко дорівнювати йому нулю, оскільки це означало б, що випадковий експеримент просто досягає теоретичної ймовірності, що дуже малоймовірно.