Як виконати одновибірковий t-тест на калькуляторі ti-84

Одновибірковий t-критерій використовується, щоб перевірити, чи дорівнює середнє значення сукупності певному значенню.

У цьому підручнику пояснюється, як виконати одновибірковий t-тест на калькуляторі TI-84.

Приклад: зразок t тесту на калькуляторі TI-84

Дослідники хочуть знати, чи може певний тип автомобіля розвивати швидкість 20 миль на галон. Вони отримують випадкову вибірку з 74 автомобілів і виявляють, що середній показник становить 21,29 милі на галон, тоді як стандартне відхилення становить 5,78 милі на галон. Використовуйте ці дані, щоб виконати одновибірковий t-тест, щоб визначити, чи справжня витрата миль на галон для цього типу автомобіля дорівнює 20 милям на галон.

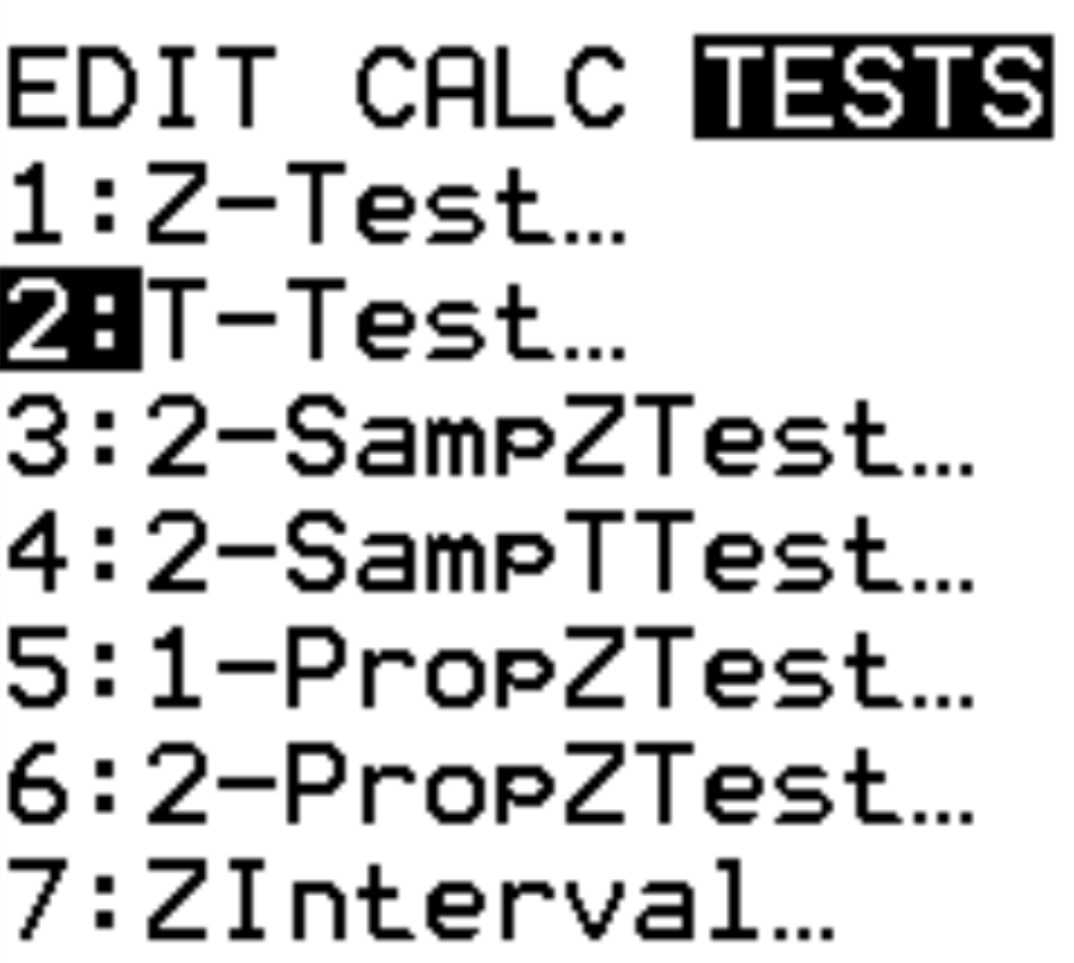
Крок 1: Виберіть T Test.

Торкніться Статистика . Прокрутіть униз до ТЕСТІВ. Перейдіть до T-Test і натисніть ENTER .

Крок 2: Заповніть необхідну інформацію.

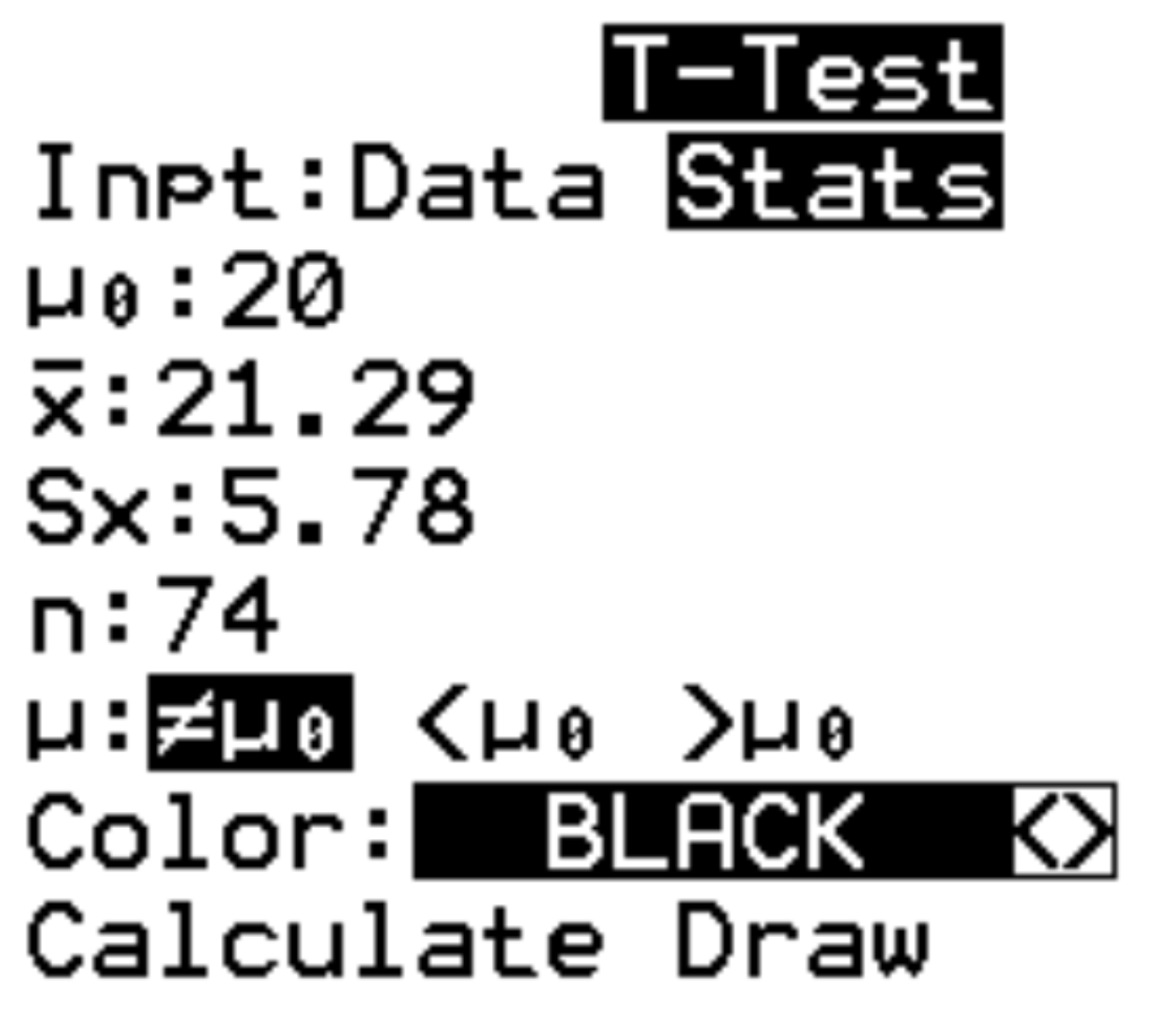
Калькулятор запитає таку інформацію:

• Введення: виберіть, чи працюєте ви з необробленими даними (Data) чи підсумковою статистикою (Stats). У цьому випадку ми виділимо Статистика та натиснемо ENTER .
• μ ₀ : середнє значення для використання в нульовій гіпотезі. Введемо 20 і натиснемо ENTER .
• x : вибірка означає. Ми введемо 21.29 і натиснемо ENTER .
• s _x : стандартне відхилення вибірки. Ми введемо 5.78 і натиснемо ENTER .
• n : розмір вибірки. Ми введемо 74 і натиснемо ENTER .
• μ : альтернативна гіпотеза для використання. Оскільки ми виконуємо двобічний тест, ми виділимо ≠ μ ₀ і натиснемо ENTER . Це означає, що наша альтернативна гіпотеза μ≠20. Інші два варіанти використовуватимуться для лівих тестів (<μ ₀ ) і правих тестів (>μ ₀ ) .

Нарешті виділіть Calculate і натисніть ENTER .

Крок 3: Інтерпретація результатів.

Наш калькулятор автоматично видасть результати одновибіркового t-критерію:

Ось як інтерпретувати результати:

• μ≠20 : це альтернативна гіпотеза тесту.
• t=1,919896124 : це t-критерій статистики.
• p=0,0587785895 : це p-значення, яке відповідає тестовій статистиці.
• х =21,59 . Це середній зразок, який ми зібрали.
• _sx =5,78 . Це стандартне відхилення зразка, яке ми ввели.
• n=74 : це розмір вибірки, який ми ввели.

Оскільки p-значення тесту (0,0587785895) не менше 0,05, ми не можемо відхилити нульову гіпотезу. Це означає, що ми не маємо достатньо доказів, щоб стверджувати, що середня витрата миль на галон для цього типу автомобіля є чимось іншим, ніж 20 миль на галон.