Імовірність перетину подій

за Редакція 1 Серпня, 2023 Ймовірність 0 коментарів

У цій статті пояснюється, як обчислити ймовірність перетину подій. Так ви дізнаєтесь, що таке формула ймовірності перетину подій і, крім того, вправи, розв’язані покроково.

Що таке перетин подій?

У теорії ймовірностей перетин подій — це операція подій, результат якої складається з елементарних подій, спільних для всіх подій операції. Тобто перетин подій А і В утворено всіма подіями, які належать А і В одночасно.

Перетин двох подій позначається символом ⋂. Отже, перетин подій A і B записується A⋂B.

Наприклад, у випадковому експерименті з киданням кубика, якщо однією подією є викидання парного числа A={2, 4, 6}, а іншою подією є викидання числа, більшого за три, B={4, 5, 6 }, то перетин двох подій є A⋂B={4, 6}.

Формула ймовірності перетину подій

Імовірність перетину двох подій дорівнює ймовірності настання однієї події, помноженій на умовну ймовірність настання іншої події з урахуванням першої події.

Отже, формула ймовірності перетину двох подій має вигляд P(A⋂B)=P(A) P(B|A)=P(B) P(A|B).

$P(A\cap B)=P(A)\cdot P(B|A)=P(B)\cdot P(A|B)$

золото:

$A$

І

$B$

Це дві залежні події.
$P(A\cap B)$

це ймовірність перетину подій A і B.
$P(A)$

це ймовірність того, що подія А відбудеться.
$P(B|A)$

це умовна ймовірність події B, що відбудеться за даної події A.
$P(B)$

це ймовірність того, що подія B відбудеться.
$P(A|B)$

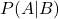
є умовною ймовірністю події A, якщо дана подія B.

➤ Див.: Умовна ймовірність (або умовна ймовірність)

Однак, якщо дві події незалежні, це означає, що ймовірність настання однієї події не залежить від того, чи відбудеться інша подія. Отже, формула ймовірності перетину двох незалежних подій має такий вигляд:

$P(A\cap B)=P(A)\cdot P(B)$

золото:

$A$

І

$B$

Це дві незалежні події.
$P(A\cap B)$

це ймовірність перетину подій A і B.
$P(A)$

це ймовірність того, що подія А відбудеться.
$P(B)$

це ймовірність того, що подія B відбудеться.

➤ Див.: Незалежні події

Реальні приклади ймовірності перетину подій

Далі ми залишаємо вам два приклади, розв’язані крок за кроком, щоб ви могли побачити, як обчислюється ймовірність перетину двох подій. Спочатку ми побачимо приклад перетину двох незалежних подій, а потім двох залежних подій, щоб ви могли бачити обидва випадки.

Імовірність перетину двох незалежних подій

Розіграш запускається три рази поспіль. Знайти ймовірність отримання голів за всі три підкидання.

У цьому випадку події, для яких ми хочемо обчислити спільну ймовірність, незалежні, оскільки результат жеребкування не залежить від результату, отриманого в попередньому жеребкуванні. Тому, щоб визначити ймовірність отримання трьох послідовних голів, ми повинні використовувати формулу ймовірності перетину для незалежних подій:

$P(A\cap B)=P(A)\cdot P(B)$

При жеребкуванні можливі лише два результати, ми можемо отримати орла або решку. Таким чином, ймовірність отримання орла або решки під час підкидання монети становить:

$P(\text{cara})=\cfrac{1}{2}=0,5$

Отже, щоб знайти ймовірність отримання голів при всіх трьох підкиданнях монети, нам потрібно помножити ймовірність отримання голів на три:

$\begin{aligned}P(\text{cara}\cap \text{cara}\cap \text{cara})&=P(\text{cara})\cdot P(\text{cara})\cdot P(\text{cara})\\[2ex]&=0,5\cdot 0,5\cdot 0,5\\[2ex]&=0,125\end{aligned}$

Коротше кажучи, ймовірність отримати голови три рази поспіль становить 12,5%.

Імовірність перетину двох залежних подій

У порожню коробку кладемо 8 синіх куль, 4 помаранчевих і 2 зелених кульки. Якщо ми спочатку витягнемо одну кулю, а потім іншу, не кладучи першу витягнуту назад у коробку, яка ймовірність того, що перша куля буде синьою, а друга помаранчевою?

У цьому випадку події є залежними, тому що ймовірність підібрати помаранчеву кульку в другому розіграші залежить від кольору кулі, витягнутої в першому розіграші. Тому, щоб обчислити ймовірність, яку нам задає задача, ми повинні використовувати формулу ймовірності перетину для залежних подій:

$P(A\cap B)=P(A)\cdot P(B|A)$

Імовірність отримати синю кульку в першому розіграші легко визначити, просто розділіть кількість синіх кульок на загальну кількість кульок:

$P(\text{bola azul})=\cfrac{8}{8+4+2}=\cfrac{8}{14}=0,57$

З іншого боку, ймовірність витягнути помаранчеву кулю після взяття синьої обчислюється по-іншому, оскільки кількість помаранчевих куль інша, і, крім того, тепер на одну кулю менше в коробці:

$P(\text{bola naranja}|\text{bola azul})=\cfrac{4}{7+4+2}=\cfrac{4}{13}=0,31$

Таким чином, ймовірність того, що спочатку буде витягнута синя кулька, а потім помаранчева, обчислюється шляхом множення двох знайдених вище ймовірностей:

$\begin{array}{l}P(\text{bola azul}\cap\text{bola naranja})=\\[2ex]=P(\text{bola azul})\cdot P(\text{bola naranja}|\text{bola azul})=\\[2ex]=0,57\cdot 0,31= \\[2ex]=0,18\end{array}$

➤ Див.: Ймовірність об’єднання подій

Властивості перетину подій

У теорії ймовірностей перетин подій має такі властивості:

Комутативна властивість: порядок подій перетину не змінює результат операції.

$A\cap B=B\cap A$

Асоціативна властивість: перетин трьох подій можна обчислити в будь-якому порядку, оскільки результат однаковий.

$(A\cap B)\cap C=A\cap (B\cap C)$

Властивість розподілу: перетин подій задовольняє властивість розподілу в об’єднанні подій.

$A\cap (B\cup C)=(A\cap B)\cup (A\cap C)$

➤ Див.: Операції з подіями

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше