Як розрахувати коефіцієнт кореляції на калькуляторі ti-84
Коефіцієнт кореляції є мірою лінійного зв’язку між двома змінними. Він може приймати значення від -1 до 1, де:
- -1 вказує на абсолютно негативну лінійну кореляцію між двома змінними
- 0 означає відсутність лінійної кореляції між двома змінними
- 1 вказує на абсолютно позитивну лінійну кореляцію між двома змінними
Щоб обчислити коефіцієнт кореляції між двома змінними на калькуляторі TI-84, можна виконати наступні кроки:
Крок 1. Увімкніть діагностику.
По-перше, нам потрібно включити діагностику. Щоб зробити це, натисніть 2nd , а потім натисніть цифру 0. Це переведе нас на екран КАТАЛОГУ.

Прокрутіть до DiagnosticOn і натисніть ENTER .
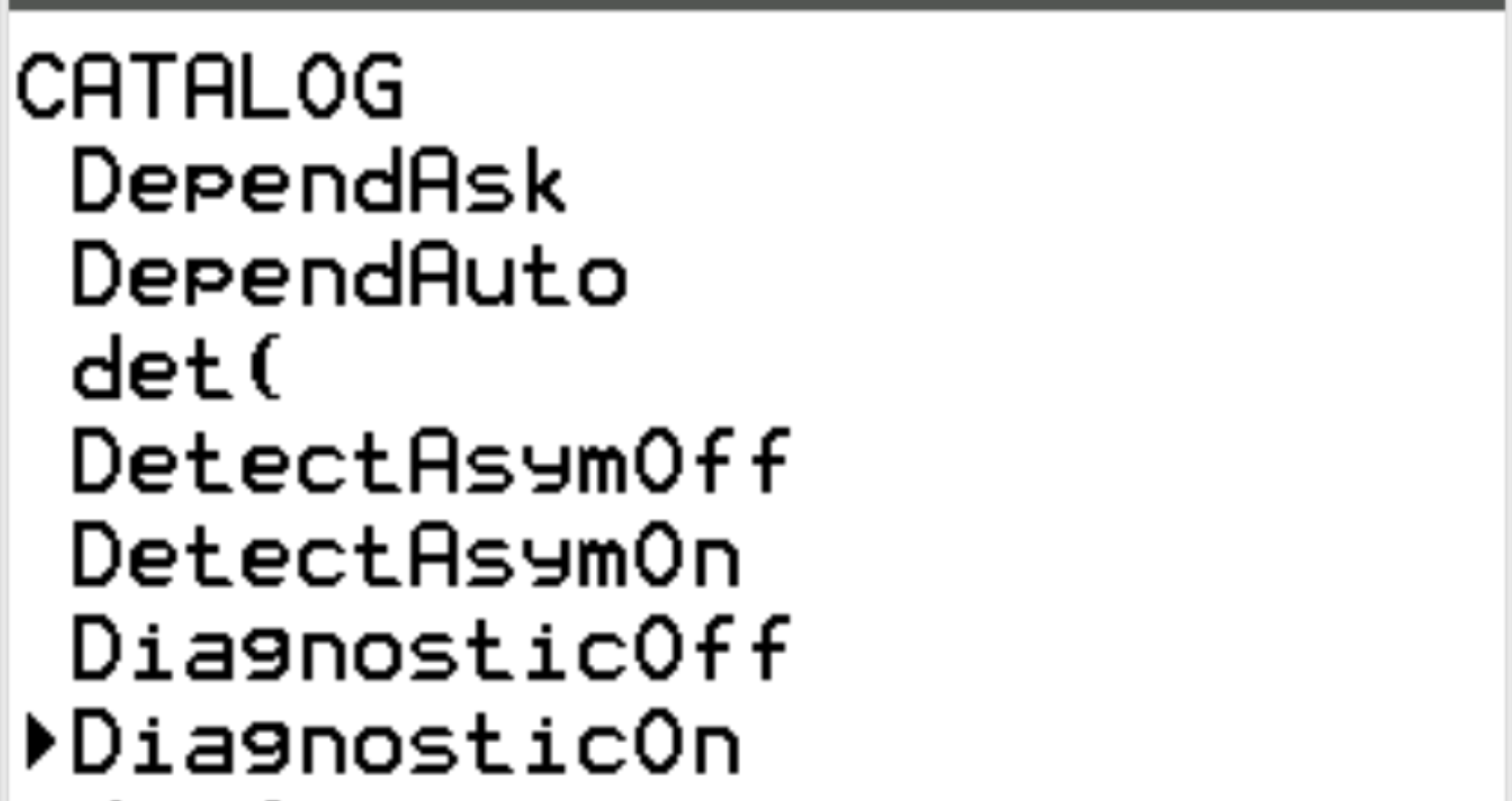
Потім знову натисніть ENTER .
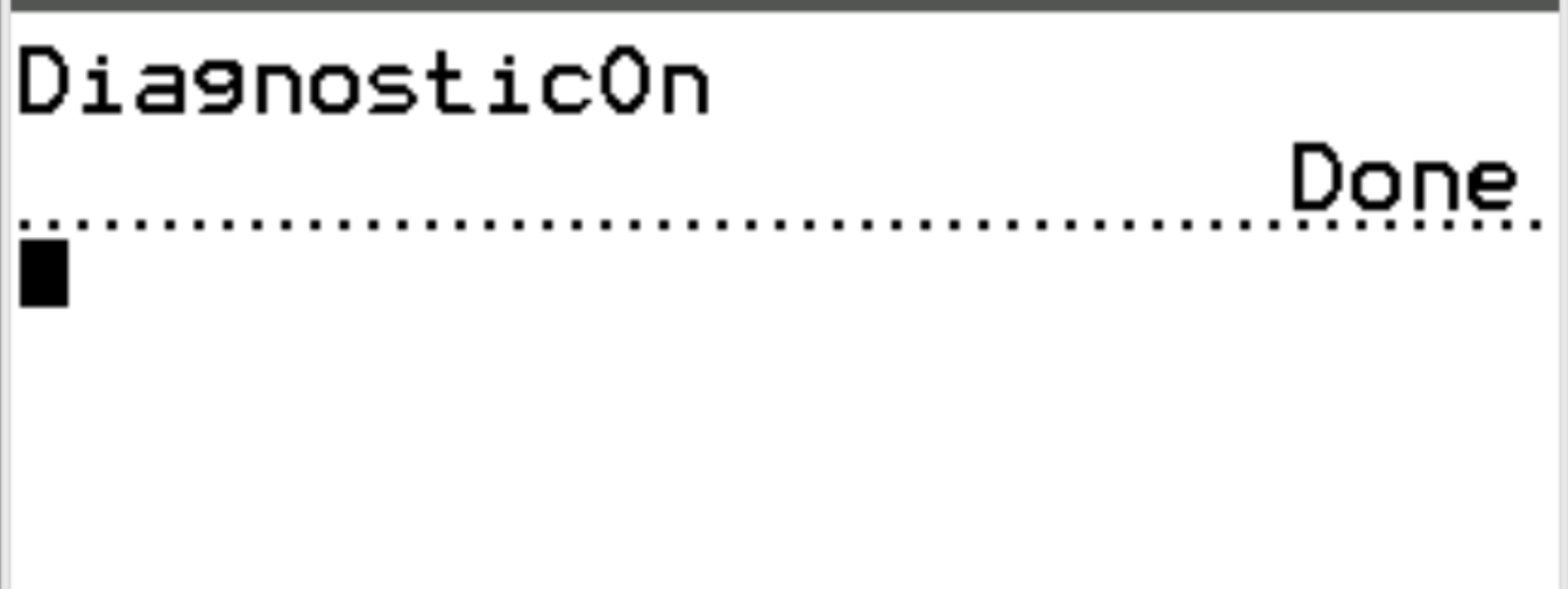
Тепер увімкнено діагностику, тому ми можемо обчислити коефіцієнт кореляції між двома змінними.
Крок 2: Введіть дані.
Далі нам потрібно ввести значення даних для наших двох змінних. Натисніть Stat, потім натисніть EDIT . Введіть значення першої змінної в стовпець L1 і значення другої змінної в стовпець L2:
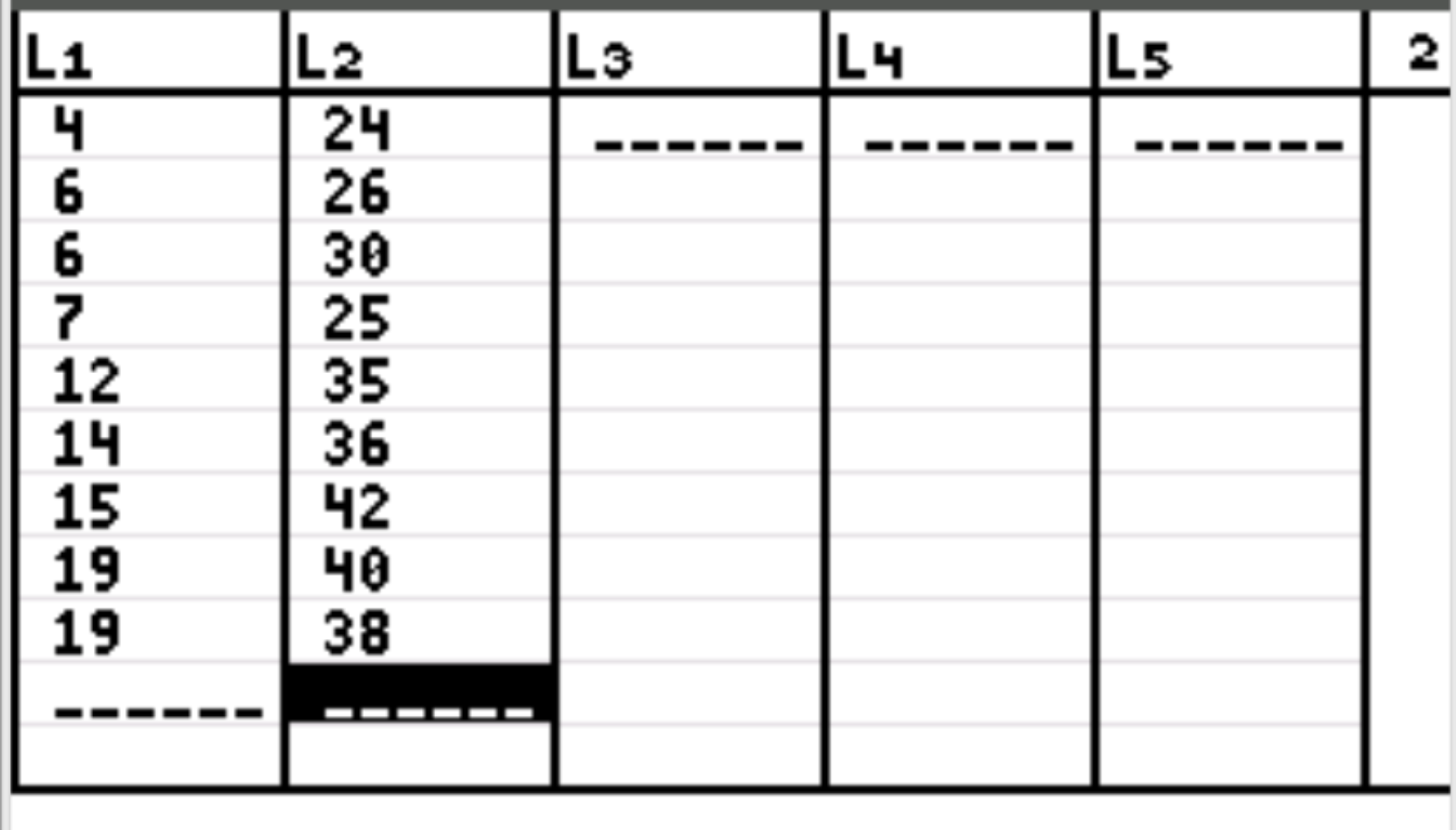
Крок 3: Знайдіть коефіцієнт кореляції.
Далі ми розрахуємо коефіцієнт кореляції між двома змінними. Натисніть Stat, а потім перейдіть до CALC . Потім прокрутіть до 8: Linreg(a+bx) і натисніть Enter .
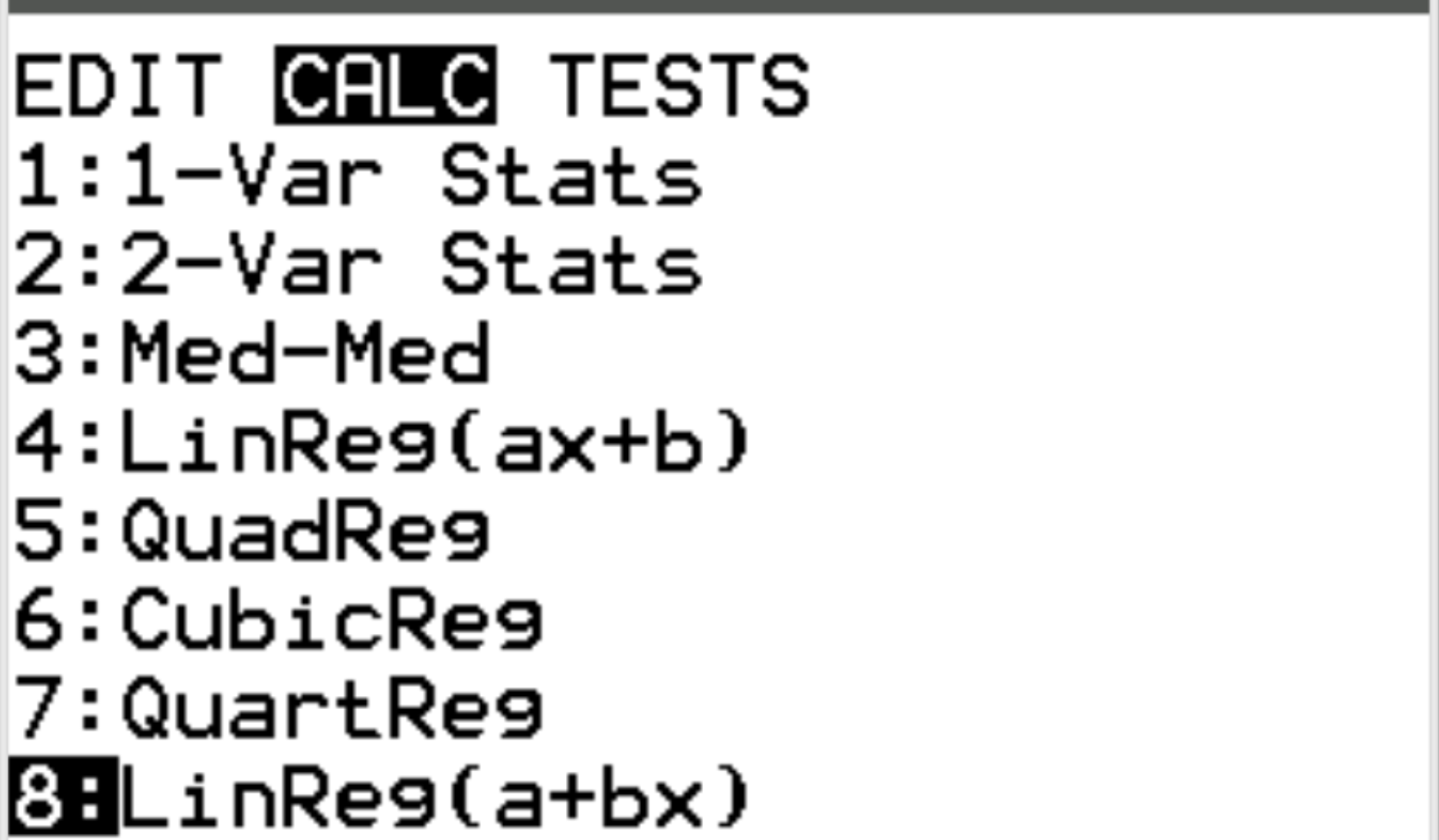
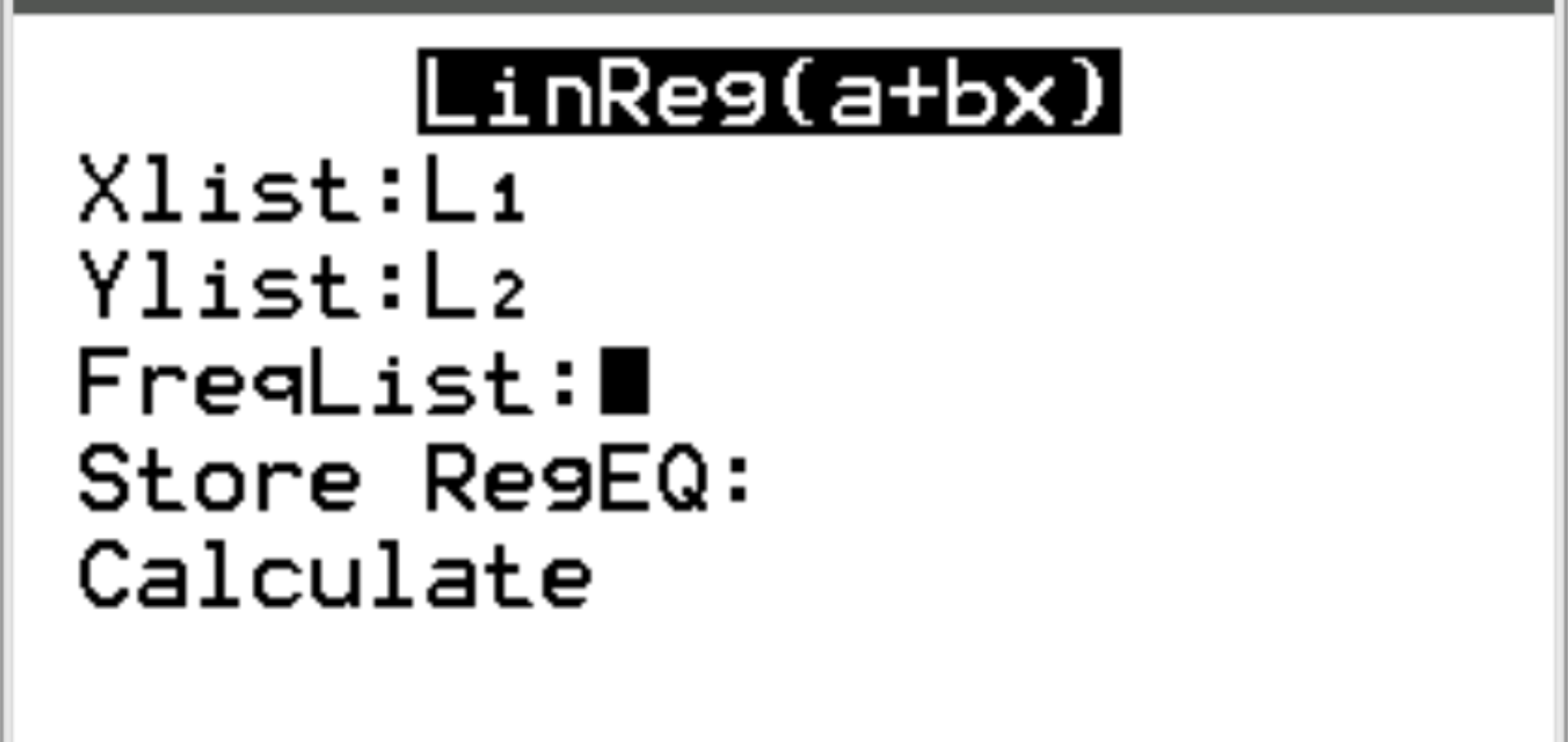
Для Xlist і Ylist переконайтеся, що вибрано L1 і L2, оскільки це стовпці, які ми використовували для введення наших даних. Залиште FreqList порожнім. Прокрутіть униз до пункту «Обчислити» та натисніть «Enter» .
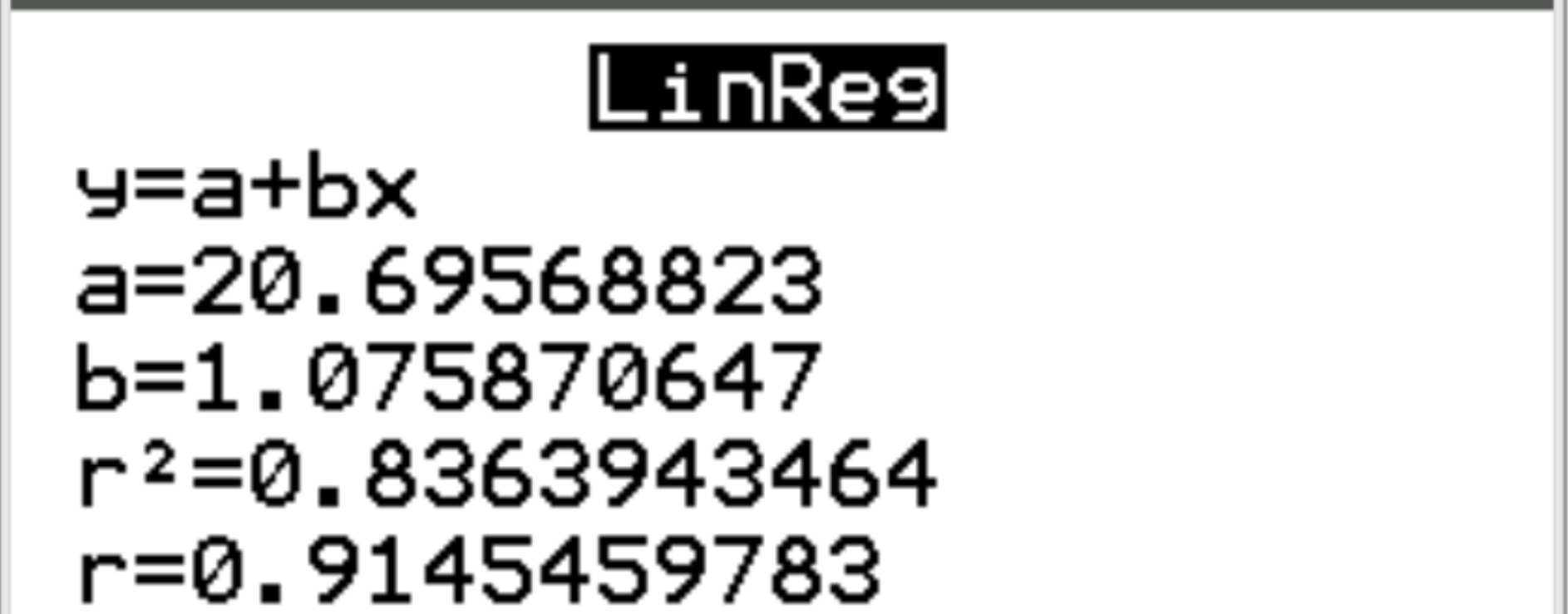
На новому екрані ми бачимо, що коефіцієнт кореляції (r) між двома змінними становить 0,9145 .
Як інтерпретувати коефіцієнт кореляції
У наведеній нижче таблиці показано емпіричне правило для інтерпретації сили зв’язку між двома змінними на основі значення r :
| Абсолютне значення r | Міцність відносин |
|---|---|
| r < 0,25 | Жодних стосунків |
| 0,25 < r < 0,5 | Слабкі стосунки |
| 0,5 < r < 0,75 | Помірні стосунки |
| r > 0,75 | Міцні відносини |
У нашому прикладі коефіцієнт кореляції 0,9145 вказує на сильний позитивний зв’язок між двома змінними.