Квазістандартне відхилення

за Редакція 3 Серпня, 2023 Статистика 0 коментарів

У цій статті пояснюється, що таке квазістандартне відхилення в статистиці та як воно обчислюється. Тож ви знайдете формулу квазістандартного відхилення, розв’язану вправу та, крім того, онлайн-калькулятор для розрахунку квазістандартного відхилення будь-якого набору даних.

Що таке квазістандартне відхилення?

У статистиці квазістандартне відхилення є мірою дисперсії, яка вказує на мінливість вибірки. Зокрема, квазістандартне відхилення дорівнює квадратному кореню із суми квадратів відхилень, поділеної на загальну кількість точок даних мінус один.

Символом квазістандартного відхилення є σ _n-1 os _n-1 .

Квазістандартне відхилення також може називатися квазістандартним відхиленням , а також іноді називається стандартним відхиленням вибірки, оскільки воно зазвичай обчислюється з використанням значень із статистичної вибірки. Нижче ми детально розглянемо різницю між квазістандартним відхиленням і стандартним відхиленням.

Формула квазістандартного відхилення

Квазістандартне відхилення дорівнює кореню квадратному із суми квадратів відхилень ряду даних, поділеного на загальну кількість спостережень мінус один. Таким чином, формула для розрахунку квазістандартного відхилення є:

золото:

$\sigma_{n-1}$

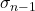
Це квазістандартне відхилення.
$x_i$

це значення даних

$i$

.
$n$

це загальна кількість даних.
$\overline{x}$

є середнім значенням набору даних.

👉 Ви можете скористатися калькулятором нижче, щоб обчислити квазістандартне відхилення для будь-якого набору даних.

Приклад розрахунку квазістандартного відхилення

Розглядаючи визначення квазістандартного відхилення, нижче ви можете побачити простий приклад того, як обчислити квазістандартне відхилення набору даних.

Бюджет компанії для відділу досліджень і розробок є дуже мінливим, оскільки він залежить від економічного прибутку, який компанія отримала в попередньому році. Таким чином, бюджет цього розділу за останні п’ять років склав: 3, 6, 2, 9, 4 мільйони євро. Обчисліть квазістандартне відхилення цього ряду даних.

Перше, що нам потрібно зробити, щоб визначити квазістандартне відхилення, це обчислити середнє арифметичне вибірки. Для цього ми складаємо всі дані і ділимо на загальну кількість спостережень, тобто п’ять:

$\overline{x}=\cfrac{3+6+2+9+4}{5}=4,8$

Далі ми застосовуємо формулу квазістандартного відхилення:

$\displaystyle\sigma_{n-1}=\sqrt{\frac{\displaystyle\sum_{i=1}^n(x_i-\overline{x})^2}{n-1}}$

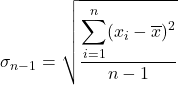
Підставляємо дані у формулу:

$\displaystyle \sigma_{n-1}=\sqrt{\frac{(3-4,8)^2+(6-4,8)^2+(2-4,8)^2+(9-4,8)^2+(4-4,8)^2}{5-1}}$

І, нарешті, обчислюємо квазістандартне відхилення:

$\begin{aligned}\displaystyle\sigma_{n-1} & = \sqrt{\frac{(-1,8)^2+1,2^2+(-2,8)^2+4,2^2+(-0,8)^2}{5-1}}\\[2ex]&=\sqrt{\frac{3,24+1,44+7,84+17,64+0,64}{4}}\\[2ex]&= \sqrt{\frac{30,8}{4}}=\sqrt{7,7}=2,77 \end{aligned}$

Коротше кажучи, квазістандартне відхилення вибірки даних становить 2,77 мільйона.

➤ Див.: Квазіваріантність

Калькулятор квазістандартного відхилення

Підключіть набір статистичних даних до онлайн-калькулятора нижче, щоб обчислити його квазістандартне відхилення. Дані повинні бути розділені пробілом і введені крапкою як десятковим роздільником.

Квазістандартне відхилення та стандартне відхилення

Нарешті, ми побачимо, у чому різниця між квазістандартним відхиленням і стандартним відхиленням, оскільки це два різні статистичні показники, які мають дуже схожу назву та обчислюються дуже схожим способом.

Різниця між квазістандартним відхиленням і стандартним відхиленням є знаменником формули. Щоб обчислити квазістандартне відхилення, розділіть на n-1, але стандартне відхилення обчислюється шляхом ділення на n.

Отже, квазістандартне відхилення та стандартне відхилення математично пов’язані, оскільки квазістандартне відхилення еквівалентно стандартному відхиленню, помноженому на квадратний корінь із n (загальна кількість точок даних) на n-1.

$\displaystyle\sigma_{n-1}=\sqrt{\frac{n}{n-1}}\cdot \sigma$

З попереднього рівняння можна зробити висновок, що для того самого набору даних значення квазістандартного відхилення завжди буде більшим за значення стандартного відхилення.

Крім того, формула квазістандартного відхилення часто використовується для розрахунку стандартного відхилення вибірки, оскільки вона усуває зміщення. Тому квазістандартне відхилення є хорошим показником стандартного відхилення сукупності. Ось чому, роблячи статистичні висновки на основі вибірки, досить часто кажуть, що обчислюється стандартне відхилення, тоді як насправді обчислюється квазістандартне відхилення.

➤ Див.: Властивості стандартного відхилення

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше