Квазіваріантність

за Редакція 3 Серпня, 2023 Статистика 0 коментарів

У цій статті пояснюється, що таке квазіваріація в статистиці. Таким чином, ви дізнаєтесь, як розрахувати квазіваріацію, розв’язану вправу та які відмінності між квазіваріацією та дисперсією. Крім того, ви можете розрахувати квазіваріацію будь-якого набору даних за допомогою онлайн-калькулятора.

Що таке квазіваріація?

У статистиці квазіваріація — це міра дисперсії, яка вказує на мінливість вибірки. Точніше, квазіваріація дорівнює сумі квадратів відхилень, поділених на загальну кількість спостережень мінус один.

Символом квазіваріації є

$\sigma_{n-1}^2$

або

$s_{n-1}^2$

. іноді використовується також символ

$\widehat{s}^2$

для представлення квазіваріації.

Квазіваріація використовується для визначення дисперсії вибірки, уникаючи зміщення, тому її часто називають незміщеною дисперсією. Отже, квазіваріація є хорошим показником дисперсії генеральної сукупності. Фактично, під час обчислення дисперсії вибірки замість формули дисперсії часто використовується формула квазідисперсії. Нижче ми детально розглянемо різницю між цими двома статистичними показниками.

Квазіваріаційна формула

Щоб обчислити квазіваріацію, потрібно знайти суму квадратів різниць між значеннями та середнім значенням набору даних, а потім розділити її на загальну кількість даних мінус одиницю.

Отже, формула для розрахунку квазіваріації виглядає наступним чином:

золото:

$\sigma_{n-1}^2$

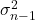
є квазіваріація.
$x_i$

це значення даних

$i$

.
$n$

це загальна кількість даних.
$\overline{X}$

є середнім значенням набору даних.

👉 Ви можете використовувати калькулятор нижче, щоб обчислити квазіваріацію будь-якого набору даних.

Вам може бути цікаво, чому воно ділиться на n-1, а не на n? Ну, мова йде про усунення зміщення, таким чином ми отримуємо неупереджену оцінку. Саме тому квазіваріантність є гарною оцінкою дисперсії сукупності.

Приклад квазіваріаційного розрахунку

Тепер, коли ми знаємо визначення квазіваріації, ми розв’яжемо простий приклад, щоб ви могли побачити, як обчислюється квазіваріація ряду даних.

Від транснаціональної компанії ми знаємо економічний результат, який вона мала за останні п’ять років, здебільшого вона отримала прибуток, але одного року вона представила значні збитки: 11,5, 2, -9, 7 мільйонів євро. Обчисліть квазіваріацію цього набору даних.

Перше, що нам потрібно зробити, щоб отримати квазіваріацію набору даних, це обчислити його середнє арифметичне:

$\overline{X}=\cfrac{11+5+2+(-9)+7}{5}=3,2$

І коли ми знаємо середнє значення даних, ми застосовуємо формулу квазіваріації:

$\sigma_{n-1}^2=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n-1}$

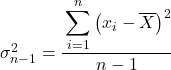
Отже, підставляємо дані, надані інструкцією до вправи, у формулу:

$\sigma_{n-1}^2=\cfrac{\displaystyle (11-3,2)^2+(5-3,2)^2+(2-3,2)^2+(-9-3,2)^2+(7-3,2)^2}{5-1}$

Нарешті, для обчислення квазіваріації достатньо вирішити операції:

$\begin{aligned}\sigma_{n-1}^2&=\cfrac{7,8^2+1,8^2+(-1,2)^2+(-12,2)^2+3,8^2}{5}\\[2ex]&=\cfrac{60,84+3,24+1,44+148,84+14,44}{5-1}\\[2ex]&= \cfrac{228,8}{4} \\[2ex]&=57,2 \ \text{millones de euros}^2\end{aligned}$

Зауважте, що одиниці квазіваріації є тими самими одиницями, що й одиниці статистичних даних, але в квадраті, тому квазіваріація цього набору даних становить 57,2 мільйона ² .

➤ Див.: Квазістандартне відхилення

Квазіваріаційний калькулятор

Введіть набір статистичних даних у наступний калькулятор, щоб обчислити його квазіваріацію. Дані повинні бути розділені пробілом і введені крапкою як десятковим роздільником.

Дисперсія та квазіваріантність

Нарешті, ми побачимо різницю між квазіваріацією та дисперсією, тому що, незважаючи на схожість назви, вони також обчислюються дуже подібно.

Різниця між квазіваріацією та дисперсією є знаменником формули. Щоб обчислити квазіваріацію, ви повинні поділити на n-1, однак дисперсія обчислюється шляхом ділення на n.

Таким чином, квазіваріація та дисперсія математично пов’язані, оскільки квазіваріація еквівалентна дисперсії, помноженій на n (загальна кількість точок даних) і поділеній на n-1.

$\sigma_{n-1}^2=\cfrac{n}{n-1}\cdot \sigma^2$

Тому для того самого набору даних значення квазіваріації завжди буде більшим за значення дисперсії.

➤ Див.: Властивості відхилень

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше