Коваріація

за Редакція 5 Серпня, 2023 Статистика 0 коментарів

У цій статті пояснюється, що таке коваріація та як вона обчислюється. Ви знайдете формулу коваріації, а також приклад обчислення коваріації набору даних. Крім того, ви можете розрахувати коваріацію будь-якого ряду даних за допомогою онлайн-калькулятора в кінці.

Що таке коваріація?

У статистиці коваріація — це значення, яке вказує на ступінь спільної варіації двох випадкових величин. Іншими словами, коваріація використовується для аналізу залежності між двома змінними.

Коваріація дорівнює сумі добутків різниць між даними двох змінних та їхніх відповідних середніх, поділених на загальну кількість даних.

👉 Ви можете скористатися калькулятором нижче, щоб обчислити коваріацію будь-якого набору даних.

Інтерпретація значення коваріації дуже проста:

Якщо коваріація додатна , це означає, що існує залежність між двома змінними. Отже, коли значення однієї змінної збільшується, інша змінна також зростає, і навпаки.
Якщо коваріація від’ємна , це означає, що зв’язок між двома змінними від’ємний. Отже, коли значення однієї змінної збільшується, інша змінна зменшується, і навпаки.
Якщо коваріація дорівнює нулю (або її значення близьке до нуля), це означає, що між двома змінними немає зв’язку. Іншими словами, дві випадкові величини незалежні.

Як розрахувати коваріацію

Щоб обчислити коваріацію ряду даних, потрібно виконати наступні кроки:

Обчисліть середнє значення кожної змінної окремо.
Для кожної змінної знайдіть різницю між кожним її значенням і середнім значенням змінної.
Помножте різниці, обчислені на попередньому кроці, для кожної точки даних.
Складіть усі результати, отримані на попередньому кроці.
Розділіть на загальну кількість даних. Отримане значення є коваріацією ряду даних.

Підсумовуючи, формула для обчислення коваріації між двома змінними виглядає наступним чином:

$Cov(X,Y)=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}$

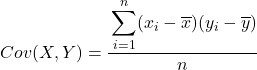
Настійно рекомендований метод вилучення коваріації між двома змінними — створити таблицю з усіма парами даних і додати стовпець для кожного кроку, описаного вище. Таким чином ваші розрахунки будуть набагато краще організовані, і ви краще розумітимете, що робите.

Приклад розрахунку коваріації

Розглядаючи визначення коваріації, нижче наведено покроковий приклад обчислення цього типу статистичного показника. Мета полягає в тому, щоб ви краще зрозуміли концепцію коваріації та те, як аналізувати кореляцію між двома змінними.

Обчисліть коваріацію наступного набору статистичних даних:

Спочатку нам потрібно обчислити середнє арифметичне кожної змінної. Для цього ми ділимо суму значень кожної змінної на загальну кількість даних.

$\overline{x}=\cfrac{58}{10}=5,8$

$\overline{y}=\cfrac{51}{10}=5,1$

➤ Див.: середнє арифметичне формула

Визначивши середнє значення кожної випадкової величини, ми можемо додати наступні стовпці до таблиці даних, щоб отримати коваріацію:

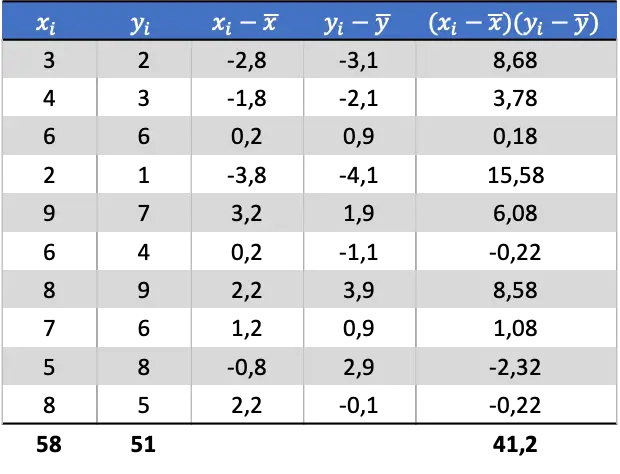
Отже, щоб визначити коваріацію двох змінних, ви повинні розділити суму останнього стовпця на кількість пар даних:

$\begin{aligned}Cov(X,Y)&=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}\\[2ex] Cov(X,Y)&= \cfrac{41,2}{10} \\[2ex]Cov(X,Y)&= 4,12\end{aligned}$

У цьому випадку значення коваріації додатне, що означає, що існує пряма залежність між двома досліджуваними випадковими змінними. Однак, якби значення коваріації було від’ємним, це означало б, що залежність між двома змінними є зворотною. І, нарешті, якщо значення коваріації дорівнює нулю або дуже близько до нуля, це означає, що між двома змінними немає лінійного зв’язку.

Як ви бачите, розв’язуючи цей приклад, дуже корисно використовувати комп’ютерну програму, наприклад Excel, щоб додати стовпці до таблиці та швидко виконати обчислення. Інакше, обчислюючи операції вручну, пошук коваріації займе набагато більше часу.

Калькулятор коваріації

Введіть набір статистичних даних у наступний калькулятор, щоб обчислити коваріацію між двома змінними. Потрібно розділити пари даних так, щоб у першому полі були лише значення однієї змінної, а в другому – лише значення другої змінної.

Дані повинні бути розділені пробілом і введені крапкою як десятковим роздільником.

Коваріаційні властивості

Коваріація має такі властивості:

Коваріація між випадковою величиною та константою дорівнює нулю.

$Cov(X,a)=0$

Коваріація змінної та сама по собі еквівалентна дисперсії цієї змінної.

$Cov(X,X)=Var(X)$

➤ Дивіться: що таке дисперсія?

Коваріація задовольняє властивість симетрії, тому коваріація змінних X і Y дорівнює коваріації змінних Y і X. Порядок змінних не впливає на результат коваріації.

$Cov(X,Y)=Cov(Y,X)$

Якщо змінні помножити на константи, ви можете спочатку обчислити коваріацію, а потім помножити результат на константи.

$Cov(a\cdot X,b\cdot Y)=a\cdot b\cdot Cov(X,Y)$

Додавання членів до змінних не впливає на результат коваріації.

$Cov(a+X,b+Y)=Cov(X+Y)$

Коваріація між двома випадковими величинами пов’язана з їхніми математичними очікуваннями. Коваріація між змінними X і Y дорівнює математичного сподівання добутку X і Y мінус добуток математичного сподівання кожної змінної.

$Cov(X,Y)=E[X\cdot Y]-E[X]\cdot E[Y]$

При роботі зі змінними наступний алгебраїчний вираз заповнюється відносно коваріації:

$\begin{aligned}\displaystyle Cov(aX+bY,cW+dV)= \ & \displaystyle acCov(X,W)+adCov(X,V)+\\[2ex]& +bcCov(Y,W)+bdCov(Y,V)\end{aligned}$

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше