Коефіцієнт кореляції пірсона

Коефіцієнт кореляції Пірсона (також відомий як «коефіцієнт кореляції продукт-момент») є мірою лінійного зв’язку між двома змінними X і Y. Він має значення від -1 до 1, де:

• -1 вказує на абсолютно негативну лінійну кореляцію між двома змінними
• 0 означає відсутність лінійної кореляції між двома змінними
• 1 вказує на абсолютно позитивну лінійну кореляцію між двома змінними

Формула для знаходження коефіцієнта кореляції Пірсона

Формула для визначення коефіцієнта кореляції Пірсона, позначеного як r , для вибірки даних ( через Вікіпедію ):

Ймовірно, вам ніколи не доведеться обчислювати цю формулу вручну, оскільки ви можете скористатися програмним забезпеченням, яке зробить це за вас, але корисно зрозуміти, що саме робить ця формула, пройшовши приклад.

Припустимо, що ми маємо наступний набір даних:

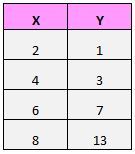
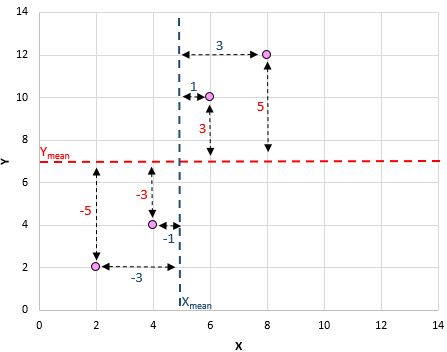
Якщо ми нанесемо ці пари (X, Y) на діаграму розсіювання, це виглядатиме так:

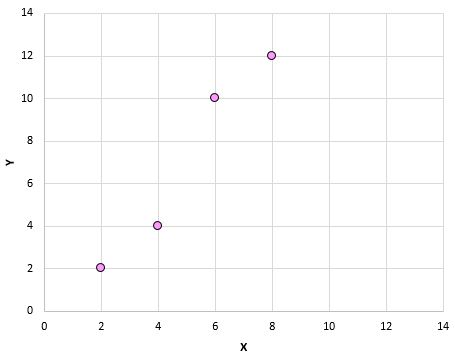
Просто подивившись на цю діаграму розсіювання, ми можемо побачити, що існує позитивний зв’язок між змінними X і Y: коли X зростає, Y також має тенденцію до зростання. Але щоб кількісно визначити, наскільки позитивно пов’язані ці дві змінні, нам потрібно знайти коефіцієнт кореляції Пірсона.

Зупинимося лише на чисельнику формули:

Для кожної пари (X, Y) у нашому наборі даних нам потрібно знайти різницю між значенням x і середнім значенням x, різницю між значенням y і середнім значенням y, а потім помножити ці два числа разом.

Наприклад, наша перша пара (X, Y) – це (2, 2). Середнє значення x у цьому наборі даних дорівнює 5, а середнє значення y у цьому наборі даних дорівнює 7. Отже, різниця між значенням x цієї пари та середнім значенням x становить 2–5 = -3. Різниця між значенням y цієї пари та середнім значенням y становить 2 – 7 = -5. Тоді, коли ми перемножимо ці два числа, ми отримаємо -3 * -5 = 15.

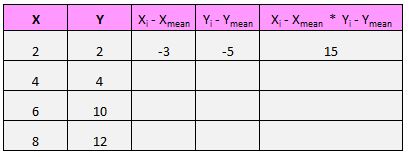
Ось візуальний огляд того, що ми щойно зробили:

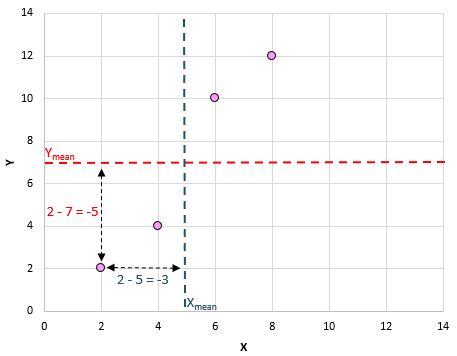
Потім просто зробіть це для кожної пари:

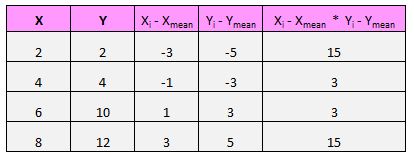
Останнім кроком для отримання чисельника формули є просто складання всіх цих значень разом:

15 + 3 +3 + 15 = 36

Тоді знаменник формули скаже нам знайти суму всіх квадратів різниць для x і y, потім помножити ці два числа разом, а потім витягти квадратний корінь:

Отже, спочатку ми знайдемо суму квадратів різниць для x і y:

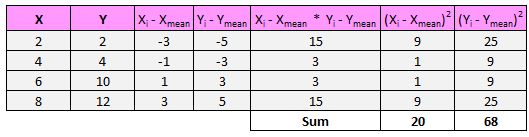
Далі ми помножимо ці два числа: 20 * 68 = 1360.

Нарешті, витягнемо квадратний корінь: √ 1360 = 36,88

Отже, ми знайшли, що чисельник формули дорівнює 36, а знаменник — 36,88. Це означає, що наш коефіцієнт кореляції Пірсона r = 36 / 36,88 = 0,976

Це число близьке до 1, що вказує на те, що між нашими змінними X і Y існує сильний позитивний лінійний зв’язок. Це підтверджує зв’язок, який ми спостерігали на діаграмі розсіювання.

Переглянути кореляції

Пам’ятайте, що коефіцієнт кореляції Пірсона вказує нам тип лінійного зв’язку (позитивний, негативний, відсутній) між двома змінними, а також силу цього зв’язку (слабкий, помірний, сильний).

Коли ми створюємо діаграму розсіювання двох змінних, ми можемо побачити реальний зв’язок між двома змінними. Ось багато типів лінійних залежностей, які ми можемо спостерігати:

Сильний позитивний зв’язок: зі збільшенням змінної на осі абсцис змінна на осі у також збільшується. Точки тісно згруповані, що вказує на міцний зв’язок.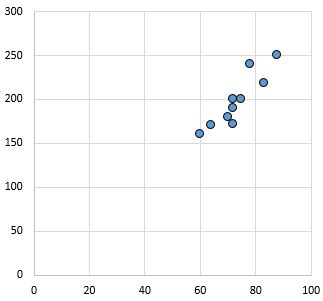

Коефіцієнт кореляції Пірсона: 0,94

Слабкий і позитивний зв’язок: зі збільшенням змінної на осі абсцис змінна на осі у також збільшується. Точки досить розкидані, що вказує на слабкий зв’язок.

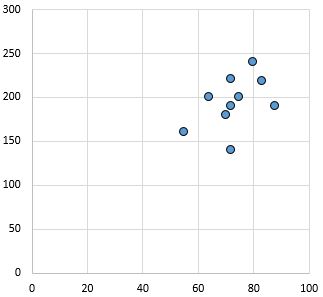
Коефіцієнт кореляції Пірсона: 0,44

Немає зв’язку: немає чіткого зв’язку (позитивного чи негативного) між змінними.

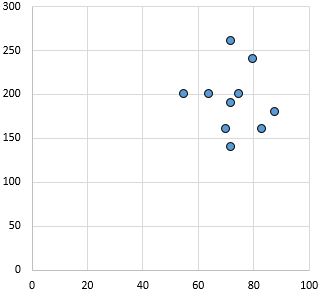
Коефіцієнт кореляції Пірсона: 0,03

Сильний, негативний зв’язок: коли змінна на осі x збільшується, змінна на осі y зменшується. Точки щільно розташовані разом, що вказує на міцні стосунки.

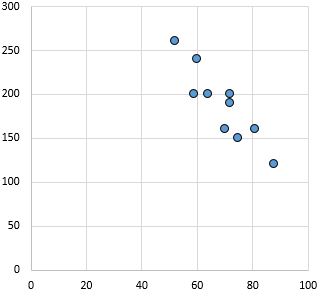
Коефіцієнт кореляції Пірсона: -0,87

Слабкий і негативний зв’язок: коли змінна на осі x збільшується, змінна на осі y зменшується. Точки досить розкидані, що вказує на слабкий зв’язок.

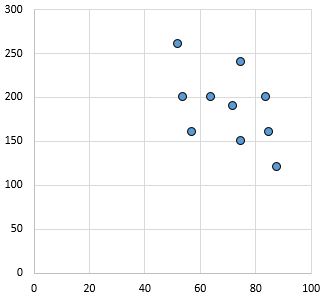
Коефіцієнт кореляції Пірсона: – 0,46

Перевірка значущості коефіцієнта кореляції Пірсона

Коли ми знаходимо коефіцієнт кореляції Пірсона для набору даних, ми часто працюємо з вибіркою даних із більшої сукупності . Це означає, що можна знайти відмінну від нуля кореляцію для двох змінних, навіть якщо вони насправді не корельовані в загальній сукупності.

Наприклад, припустімо, що ми створюємо діаграму розсіювання для змінних X і Y для кожної точки даних у всій сукупності, і вона виглядає так:

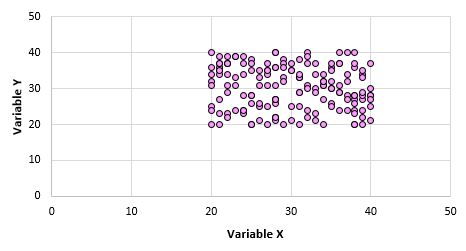
Очевидно, що ці дві змінні не корельовані. Однак можливо, коли ми беремо вибірку з 10 балів із генеральної сукупності, ми вибираємо такі точки:

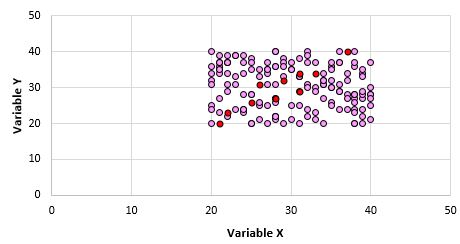
Ми бачимо, що коефіцієнт кореляції Пірсона для цієї вибірки балів становить 0,93, що вказує на сильну позитивну кореляцію, навіть якщо кореляція сукупності дорівнює нулю.

Щоб перевірити, чи кореляція між двома змінними є статистично значущою чи ні, ми можемо знайти таку тестову статистику:

Тестова статистика T = r * √ (n-2) / (1-r ² )

де n – кількість пар у нашій вибірці, r – коефіцієнт кореляції Пірсона, а статистика тесту T відповідає розподілу з n-2 ступенями свободи.

Давайте розглянемо приклад того, як перевірити значущість коефіцієнта кореляції Пірсона.

приклад

Наступний набір даних показує зріст і вагу 12 осіб:

Діаграма розсіювання нижче показує значення цих двох змінних:

Коефіцієнт кореляції Пірсона для цих двох змінних становить r = 0,836.

Статистика тесту T = 0,836 * √ (12 -2) / (1-0,836 ² ) = 4,804.

Згідно з нашим калькулятором t-розподілу , показник 4,804 з 10 ступенями свободи має p-значення 0,0007. Оскільки 0,0007 < 0,05, можна зробити висновок, що кореляція між вагою та зростом у цьому прикладі є статистично значущою при альфа = 0,05.

Запобіжні заходи

Хоча коефіцієнт кореляції Пірсона може бути корисним для визначення того, чи мають дві змінні лінійний зв’язок, ми повинні мати на увазі три речі, інтерпретуючи коефіцієнт кореляції Пірсона:

1. Кореляція не передбачає причинно-наслідкового зв’язку. Не тому, що дві змінні корельовані, одна обов’язково спричиняє більш чи менш часту появу іншої. Класичним прикладом цього є позитивна кореляція між продажем морозива та нападами акул. Коли продажі морозива збільшуються в певну пору року, напади акул також мають тенденцію до збільшення.

Чи означає це, що вживання морозива викликає напади акул? Звичайно, ні! Це просто означає, що влітку споживання льоду та напади акул, як правило, збільшуються, оскільки лід більш популярний влітку, і влітку більше людей вирушає в океан.

2. Кореляції чутливі до викидів. Екстремальний викид може значно змінити коефіцієнт кореляції Пірсона. Розглянемо приклад нижче:

Змінні X і Y мають коефіцієнт кореляції Пірсона 0,00 . Але уявіть, що в наборі даних є викид:

Однак коефіцієнт кореляції Пірсона для цих двох змінних становить 0,878 . Цей один викид змінює все. Ось чому під час обчислення кореляції для двох змінних доцільно візуалізувати змінні за допомогою діаграми розсіювання, щоб перевірити наявність викидів.

3. Коефіцієнт кореляції Пірсона не фіксує нелінійні зв’язки між двома змінними. Давайте уявімо, що ми маємо дві змінні з таким співвідношенням:

Коефіцієнт кореляції Пірсона для цих двох змінних дорівнює 0,00, оскільки вони не мають лінійного зв’язку. Однак ці дві змінні мають нелінійну залежність: значення y є просто значеннями x у квадраті.

Використовуючи коефіцієнт кореляції Пірсона, майте на увазі, що ви просто перевіряєте, чи дві змінні лінійно пов’язані. Навіть якщо коефіцієнт кореляції Пірсона говорить нам, що дві змінні не корельовані, вони все одно можуть мати певний тип нелінійного зв’язку. Це ще одна причина, чому корисно створювати діаграму розсіювання під час аналізу зв’язку між двома змінними: це може допомогти вам виявити нелінійний зв’язок.