Коефіцієнт кореляції пірсона
У цій статті пояснюється, що таке коефіцієнт кореляції Пірсона (або лінійний коефіцієнт кореляції) і для чого він використовується. Ви дізнаєтесь, як розрахувати коефіцієнт кореляції Пірсона разом із покроковою вправою. Крім того, ви можете знайти значення коефіцієнта кореляції Пірсона будь-якого набору даних за допомогою онлайн-калькулятора в кінці.
Що таке коефіцієнт кореляції Пірсона?
Коефіцієнт кореляції Пірсона , також званий лінійним коефіцієнтом кореляції або просто коефіцієнтом кореляції , є статистичним показником, який вказує на зв’язок між двома змінними.
Щоб обчислити коефіцієнт кореляції Пірсона між двома змінними, ви повинні розділити коваріацію зазначених змінних на квадратний корінь із добутку їх дисперсій.
Таким чином, коефіцієнт кореляції Пірсона намагається кількісно визначити лінійну залежність між двома кількісними випадковими величинами. Апріорі чисельно оцінити кореляцію між змінними складно, оскільки важко визначити, що пара змінних більш корельована між собою, якщо, як у pues, об’єктом коефіцієнта кореляції Пірсона є оцінка зв’язку між змінними, щоб мати можливість порівняти між собою.
Значення індексу кореляції Пірсона знаходиться в межах від -1 до +1 включно. Нижче ми побачимо, як інтерпретується значення коефіцієнта кореляції Пірсона.
Формула коефіцієнта кореляції Пірсона
Коефіцієнт кореляції Пірсона двох статистичних змінних дорівнює частці між коваріацією змінних і квадратним коренем із добутку дисперсії кожної змінної.
Отже, формула для розрахунку коефіцієнта кореляції Пірсона має такий вигляд:
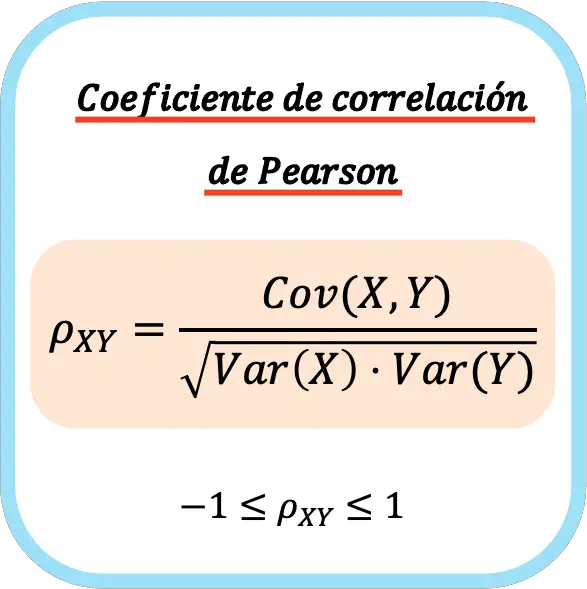
👉 Ви можете скористатися калькулятором нижче, щоб обчислити коефіцієнт кореляції Пірсона для будь-якого набору даних.
Коли коефіцієнт кореляції Пірсона обчислюється для генеральної сукупності, він зазвичай виражається грецькою літерою ρ. Але коли коефіцієнт обчислюється відносно вибірки, як символ зазвичай використовується буква r.
Майте на увазі, що для визначення коефіцієнта кореляції Пірсона важливо знати, як обчислити коваріацію між двома змінними та дисперсію змінної. Крім того, вам потрібно зрозуміти, що означають ці статистичні заходи. Тому, перш ніж продовжити пояснення, рекомендується прочитати наступні дві статті:
Приклад розрахунку коефіцієнта кореляції Пірсона
Розглядаючи визначення коефіцієнта кореляції Пірсона та його формулу, нижче наведено покроковий приклад, щоб ви могли побачити, як він обчислюється.
- Обчисліть коефіцієнт кореляції Пірсона між такими двома неперервними змінними:

Перш ніж обчислити коефіцієнт кореляції Пірсона, ми представимо набір даних у вигляді діаграми розсіювання, щоб проаналізувати зв’язок між двома змінними:
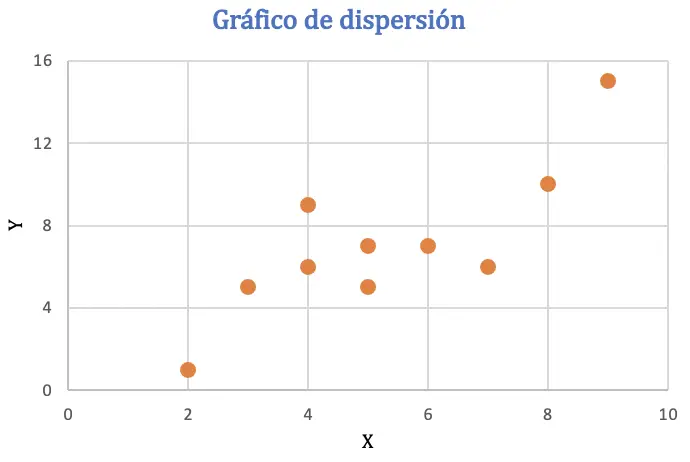
З діаграми розсіювання можна зробити висновок, що дані можуть мати позитивну тенденцію, або, іншими словами, коли значення однієї змінної збільшується, інша змінна також зростає. Щоб перевірити кореляцію, знайдемо коефіцієнт Пірсона.
Перше, що потрібно зробити, це знайти середнє арифметичне кожної змінної окремо, яке еквівалентно загальній сумі даних, поділеній на кількість спостережень.
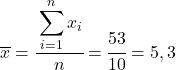
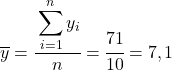
Тепер, коли ми знаємо середнє значення кожної змінної, нам потрібно додати наступні стовпці до таблиці даних:
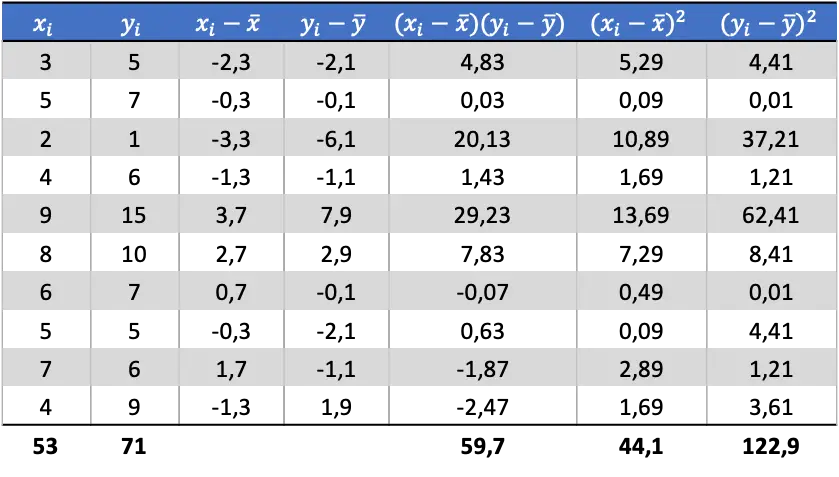
За розрахованими даними в таблиці визначаємо значення коваріації і дисперсій (якщо не пам’ятаєте, як це робилося, то вище є два посилання, де це докладно пояснено):
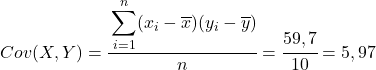
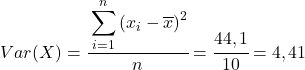
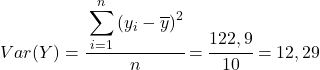
Нарешті, просто застосуйте формулу коефіцієнта кореляції Пірсона, щоб отримати його значення:
![]()
Коефіцієнт кореляції Пірсона має значення, дуже близьке до 1, що означає, що ці дві змінні мають досить сильну позитивну кореляцію.
Як ви бачили, для визначення коефіцієнта кореляції Пірсона дуже корисно використовувати такі програми, як Excel, щоб швидше виконувати обчислення стовпців.
Калькулятор коефіцієнта кореляції Пірсона
Введіть набір статистичних даних у наступний калькулятор, щоб обчислити коефіцієнт кореляції Пірсона між двома змінними. Потрібно розділити пари даних так, щоб у першому полі були лише значення однієї змінної, а в другому – лише значення другої змінної.
Дані повинні бути розділені пробілом і введені крапкою як десятковим роздільником.
Інтерпретація коефіцієнта кореляції Пірсона
У цьому розділі ми побачимо, як інтерпретувати коефіцієнт кореляції Пірсона, оскільки недостатньо знати його значення, але потрібно знати, як аналізувати його значення.
Таким чином , інтерпретація коефіцієнта кореляції Пірсона залежить від його значення:
- r=-1 : дві змінні мають ідеальну негативну кореляцію, тому ми можемо намалювати лінію з негативним нахилом, у якій усі точки пов’язані.
- -1<r<0 : кореляція між двома змінними негативна, тому коли одна змінна зростає, інша зменшується. Чим ближче значення до -1, тим більше негативно пов’язані змінні.
- r=0 : кореляція між двома змінними дуже слабка, фактично лінійна залежність між ними дорівнює нулю. Це не означає, що змінні є незалежними, оскільки вони можуть мати нелінійний зв’язок.
- 0<r<1 : кореляція між двома змінними позитивна, чим ближче значення до +1, тим сильніший зв’язок між змінними. У цьому випадку одна змінна має тенденцію до збільшення значення, коли інша також збільшується.
- r=1 : дві змінні мають ідеальну позитивну кореляцію, тобто вони мають позитивну лінійну залежність.
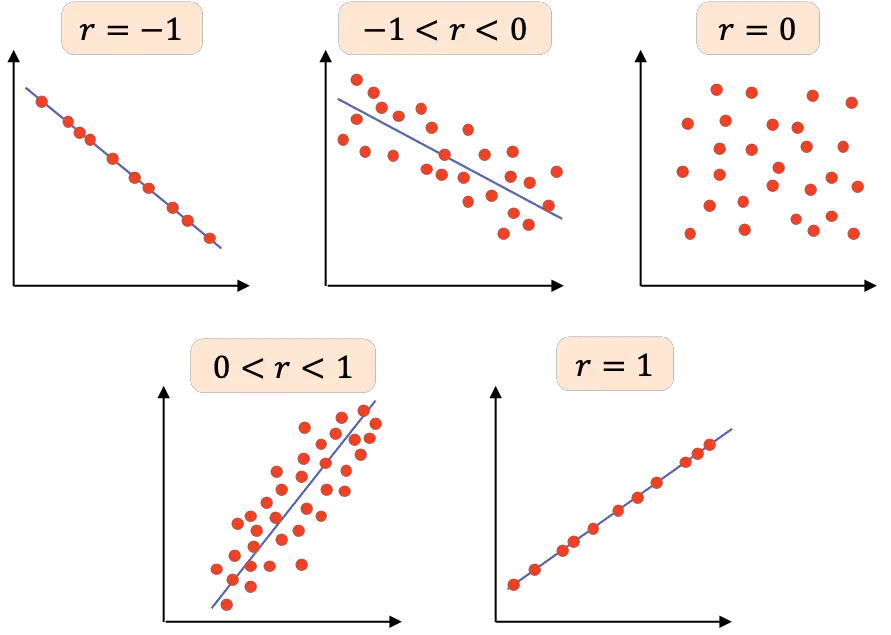
Підсумовуючи, у наступній таблиці представлено різні інтерпретації коефіцієнта кореляції Пірсона:
| Значення | Інтерпретація |
|---|---|
| r=-1 | Ідеальна негативна кореляція. |
| -1<r<0 | Негативна кореляція: чим ближча кореляція до -1, тим вона сильніша. |
| r=0 | Нульова лінійна кореляція. |
| 0<r<1 | Позитивна кореляція: чим ближча кореляція до +1, тим вона сильніша. |
| r=1 | Ідеальна позитивна кореляція. |
Майте на увазі, що навіть якщо існує зв’язок між двома змінними, це не означає, що між ними існує причинно-наслідковий зв’язок, тобто кореляція між двома змінними не означає, що зміна змінної є причиною зміни змінної. інша змінна.
Наприклад, якщо ми виявимо, що існує позитивний зв’язок між виробництвом двох різних гормонів в організмі, необов’язково, щоб підвищення рівня одного гормону призводило до збільшення рівня іншого гормону. Цілком можливо, що організм виробляє обидва гормони, оскільки йому потрібні обидва для боротьби з хворобою, і тому підвищується рівень обох одночасно, у такому випадку причиною буде хвороба. Щоб визначити, чи існує причинно-наслідковий зв’язок між двома гормонами, необхідно провести додаткові дослідження.