Коли слід використовувати коробковий графік? (3 сценарії)

Ящичний графік – це тип графіка, який відображає п’ятизначний підсумок набору даних, який включає:

• Мінімальне значення
• Перший квартиль (25-й процентиль)
• Середнє значення
• Третій квартиль (75-й процентиль)
• Максимальне значення

Ми використовуємо три прості кроки, щоб створити коробковий графік для будь-якого набору даних:

• 1. Намалюйте квадрат від першого до третього квартиля
• 2. Проведіть вертикальну лінію на серединній лінії
• 3. Намалюйте «вуса» квартилів до мінімального та максимального значення

Зазвичай ми створюємо коробкові діаграми в одному з трьох сценаріїв:

Сценарій 1: візуалізуйте розподіл значень у наборі даних.

Ящичний графік дозволяє нам швидко візуалізувати розподіл значень у наборі даних і побачити, де розташовані п’ять числових підсумкових значень.

Сценарій 2: порівняння двох або більше розподілів.

Пліч-о-пліч коробкові діаграми дозволяють нам візуалізувати відмінності між двома або більше розподілами та порівнювати медіанні значення та розподіл значень між розподілами.

Сценарій 3: Визначити викиди.

На прямокутних діаграмах викиди зазвичай представлені крихітними колами, які виходять за межі кожного вуса. Спостереження визначається як викид, якщо воно відповідає одному з наступних критеріїв:

• Спостереження менше Q1 – 1,5*(міжквартильний діапазон)
• Спостереження перевищує Q3 + 1,5*(міжквартильний діапазон)

Створивши коробковий графік, ми можемо швидко побачити, чи має розподіл викиди.

Наведені нижче приклади показують, як ми будемо використовувати коробковий графік у кожному сценарії.

Сценарій 1: візуалізуйте розподіл значень у наборі даних

Припустімо, що баскетбольний тренер хоче візуалізувати розподіл очок, набраних гравцями його команди, і тому створює такий графічний графік:

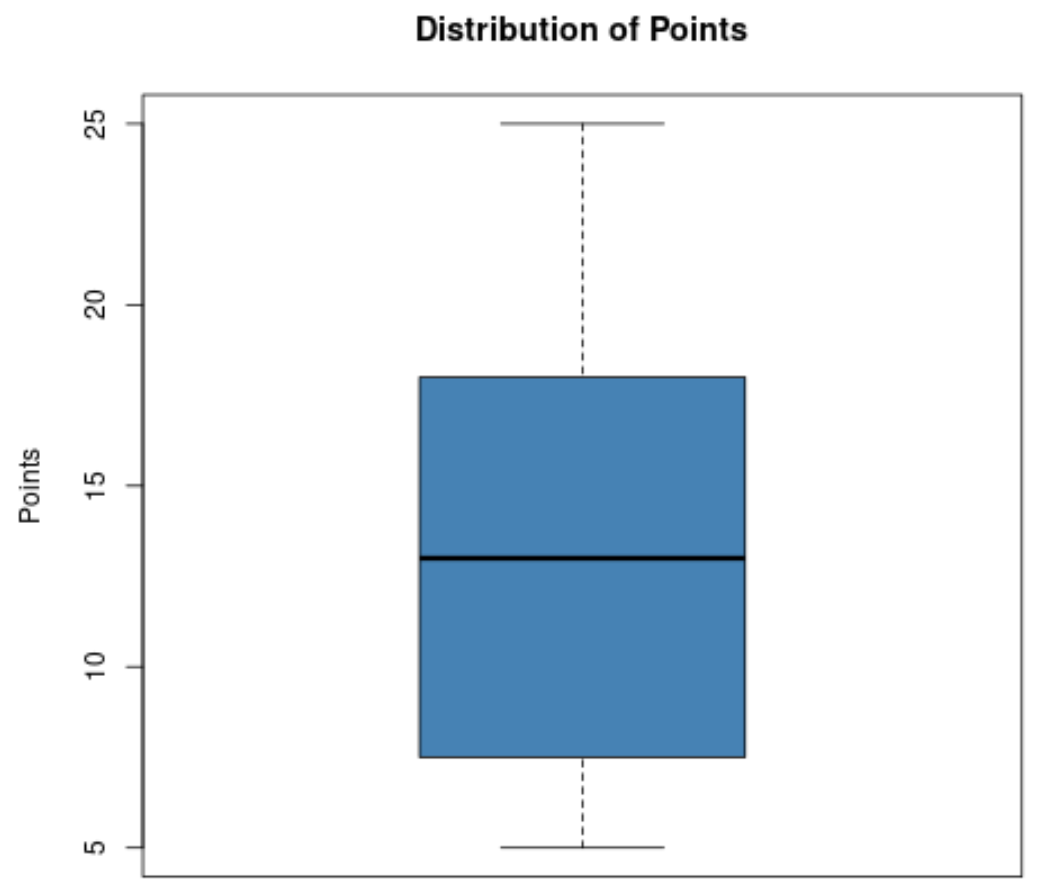
На основі цього прямокутного графіка він може швидко побачити такі значення:

• Мінімум: 5
• T1 (перший квартиль): приблизно 8
• Медіана: близько 13
• T3 (третій квартиль): приблизно 18
• Максимум: 25

Це дозволяє тренеру швидко побачити, що очки, набрані гравцями, коливаються від 5 до 25, що середня кількість набраних очок становить приблизно 13 і що 50% його гравців набирають приблизно від 8 до 18 очок за гру.

Сценарій 2. Порівняйте два або більше розподілів

Припустімо, що спортивний аналітик хоче порівняти розподіл очок, набраних баскетболістами трьох різних команд, і створює такі діаграми:

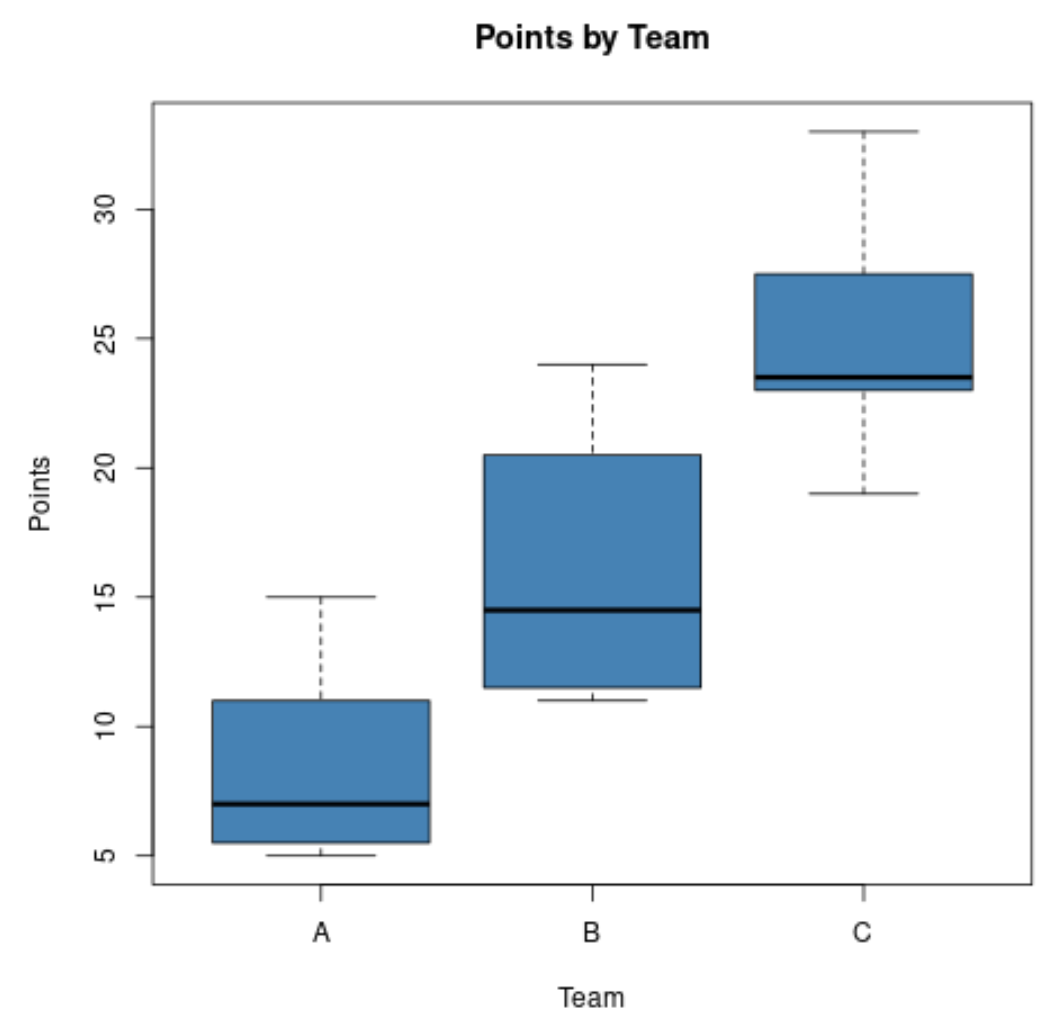
Використовуючи ці графіки, він може швидко побачити, що команда С має найвищі середні точки, а команда А має найменші середні точки.

Він також може швидко побачити, що команда B має найбільший розподіл набраних очок, оскільки діаграма коробки команди B має найдовшу коробку.

Сценарій 3: Визначте викиди

Припустімо, що баскетбольний тренер хоче знати, чи один із його гравців виділяється за кількістю набраних очок. Він вирішує створити таку коробкову діаграму, щоб візуалізувати розподіл очок, набраних його гравцями:

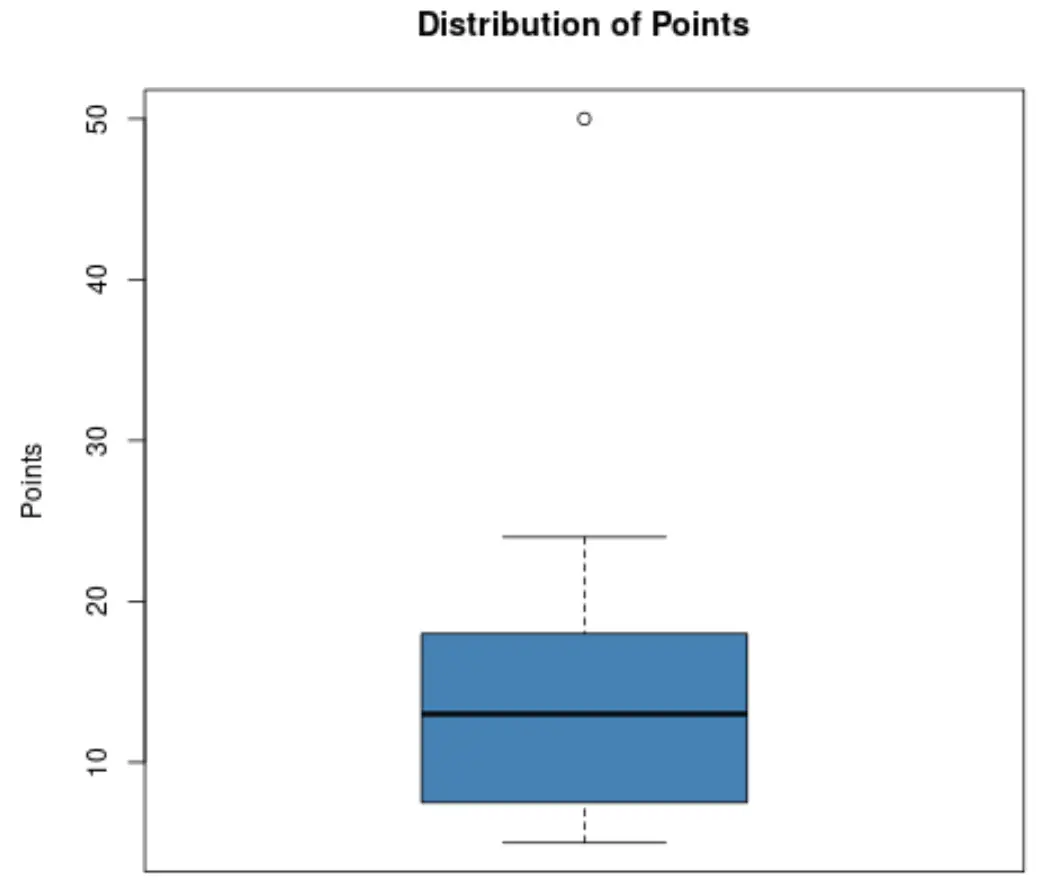
Використовуючи цей графік, тренер може побачити, що маленька точка у верхній частині графіка вказує на викид.

Зокрема, один із гравців набрав близько 50 очок, що вважається викидом порівняно з усіма іншими набраними очками.

Додаткові ресурси

Наступні навчальні посібники пропонують детальні пояснення того, як використовувати boxplots на практиці:

Як знайти інтерквартильний діапазон (IQR) прямокутної діаграми
Як визначити асиметрію на прямокутних графіках
Як порівняти коробкові діаграми

У наступних посібниках пояснюється, як створювати діаграми в різних статистичних програмах:

Як створити коробчату діаграму в Google Таблицях
Як створити коробкові діаграми в SPSS
Як створити діаграми поруч в Excel
Як створити паралельні діаграми прямокутників у R