Що таке компроміс зміщення та дисперсії в машинному навчанні?

Щоб оцінити ефективність моделі на наборі даних, нам потрібно виміряти, наскільки прогнози моделі відповідають спостережуваним даним.

Для регресійних моделей найбільш часто використовуваним показником є середня квадратична помилка (MSE), яка обчислюється таким чином:

MSE = (1/n)*Σ(y _i – f(x _i )) ²

золото:

• n: загальна кількість спостережень
• y _i : значення відповіді ^i-го спостереження
• f(x _i ): прогнозоване значення відповіді i- ^го спостереження

Чим ближче прогнози моделі до спостережень, тим нижчим буде MSE.

Однак ми дбаємо лише про тест MSE – MSE, коли наша модель застосовується до невидимих даних. Це тому, що ми дбаємо лише про те, як модель працюватиме на невідомих даних, а не на існуючих даних.

Наприклад, це добре, якщо модель, яка передбачає курси акцій, має низький MSE на історичних даних, але ми дійсно хочемо мати можливість використовувати модель для точного прогнозування майбутніх даних.

Виявляється, тест MSE все ще можна розбити на дві частини:

(1) Дисперсія: стосується величини, яку змінила б наша функція f , якби ми оцінили її за допомогою іншого навчального набору.

(2) Зміщення: відноситься до помилки, яка виникає в результаті підходу до реальної проблеми, яка може бути надзвичайно складною, за допомогою набагато простішої моделі.

Написано в математичних термінах:

Тест MSE = Var( f̂( x ₀ )) + [Зміщення( f̂( x ₀ ))] ² + Var(ε)

Тест MSE = дисперсія + зсув ² + незнижувана помилка

Третій термін, незнижувана помилка, — це помилка, яку не можна зменшити жодною моделлю просто тому, що у зв’язку між набором пояснювальних змінних і змінною відповіді завжди є шум .

Моделі з високим зміщенням, як правило, мають низьку дисперсію . Наприклад, моделі лінійної регресії, як правило, мають високу похибку (за умови простого лінійного зв’язку між пояснювальними змінними та змінною відповіді) і низьку дисперсію (оцінки моделі не сильно змінюватимуться від вибірки до вибірки). інші).

Однак моделі з низьким зміщенням, як правило, мають високу дисперсію . Наприклад, складні нелінійні моделі, як правило, мають низьке зміщення (не припускають певного зв’язку між пояснювальними змінними та змінною відповіді) з високою дисперсією (оцінки моделі можуть суттєво змінюватися від зразка навчання до іншого).

Компроміс зміщення-дисперсії

Компроміс зміщення-дисперсії відноситься до компромісу, який має місце, коли ми вирішуємо зменшити зміщення, що зазвичай збільшує дисперсію, або зменшити дисперсію, що загалом збільшує зміщення.

Наступний графік пропонує спосіб візуалізації цього компромісу:

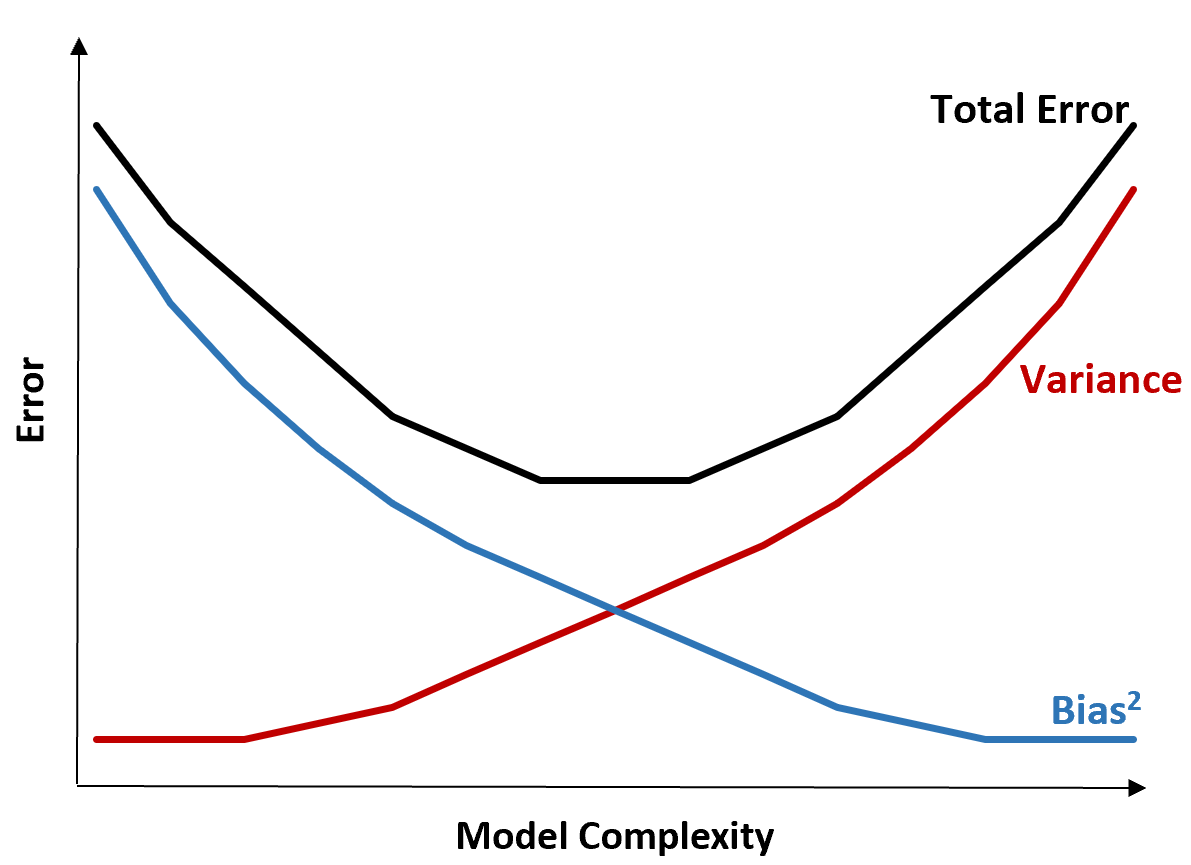
Загальна похибка зменшується зі збільшенням складності моделі, але лише до певного моменту. Після певної точки дисперсія починає збільшуватися, і загальна помилка також починає збільшуватися.

На практиці ми дбаємо лише про мінімізацію загальної похибки моделі, не обов’язково мінімізуючи дисперсію чи зміщення. Виявляється, спосіб мінімізувати загальну помилку полягає в тому, щоб знайти правильний баланс між дисперсією та зміщенням.

Іншими словами, ми хочемо досить складну модель, щоб зафіксувати справжній зв’язок між пояснювальними змінними та змінною відповіді, але не надто складну, щоб виявити шаблони, яких насправді не існує.

Коли модель надто складна, вона переповнює дані. Це відбувається через те, що надто важко знайти закономірності в навчальних даних, які просто викликані випадковістю. Цей тип моделі, ймовірно, погано працюватиме з невидимими даними.

Але коли модель занадто проста, вона занижує дані. Це відбувається тому, що передбачається, що справжній зв’язок між пояснювальними змінними та змінною відповіді простіший, ніж є насправді.

Спосіб вибору оптимальних моделей у машинному навчанні полягає в тому, щоб знайти баланс між зміщенням і дисперсією, щоб мінімізувати помилку тестування моделі на майбутніх невидимих даних.

На практиці найпоширенішим способом мінімізації MSE тестів є використання перехресної перевірки .