Як виконати корекцію бонферроні в excel
Поправка Бонферроні відноситься до процесу коригування рівня альфа (α) для групи статистичних тестів для контролю ймовірності помилки типу I.
Формула для поправки Бонферроні така:
α новий = α оригінальний / n
золото:
- вихідний α: вихідний рівень α
- n: загальна кількість виконаних порівнянь або тестів
Наприклад, якщо ми запускаємо три статистичні тести одночасно і хочемо використовувати α = 0,05 для кожного тесту, поправка Бонферроні говорить нам, що ми повинні використовувати α new = 0,01667 .
новий α = вихідний α / n = 0,05 / 3 = 0,01667
Таким чином, ми повинні відхилити нульову гіпотезу кожного окремого тесту, лише якщо р-значення тесту менше 0,01667.
Цей тип корекції часто виконується в пост-хок тестах після ANOVA, коли ми хочемо порівняти кілька групових середніх одночасно.
У наступному покроковому прикладі показано, як виконати поправку Бонферроні після одностороннього дисперсійного аналізу в Excel.
Крок 1: Створіть дані
По-перше, давайте створимо підроблений набір даних, який показує результати студентів, які використовували одну з трьох різних методів навчання для підготовки до іспиту:
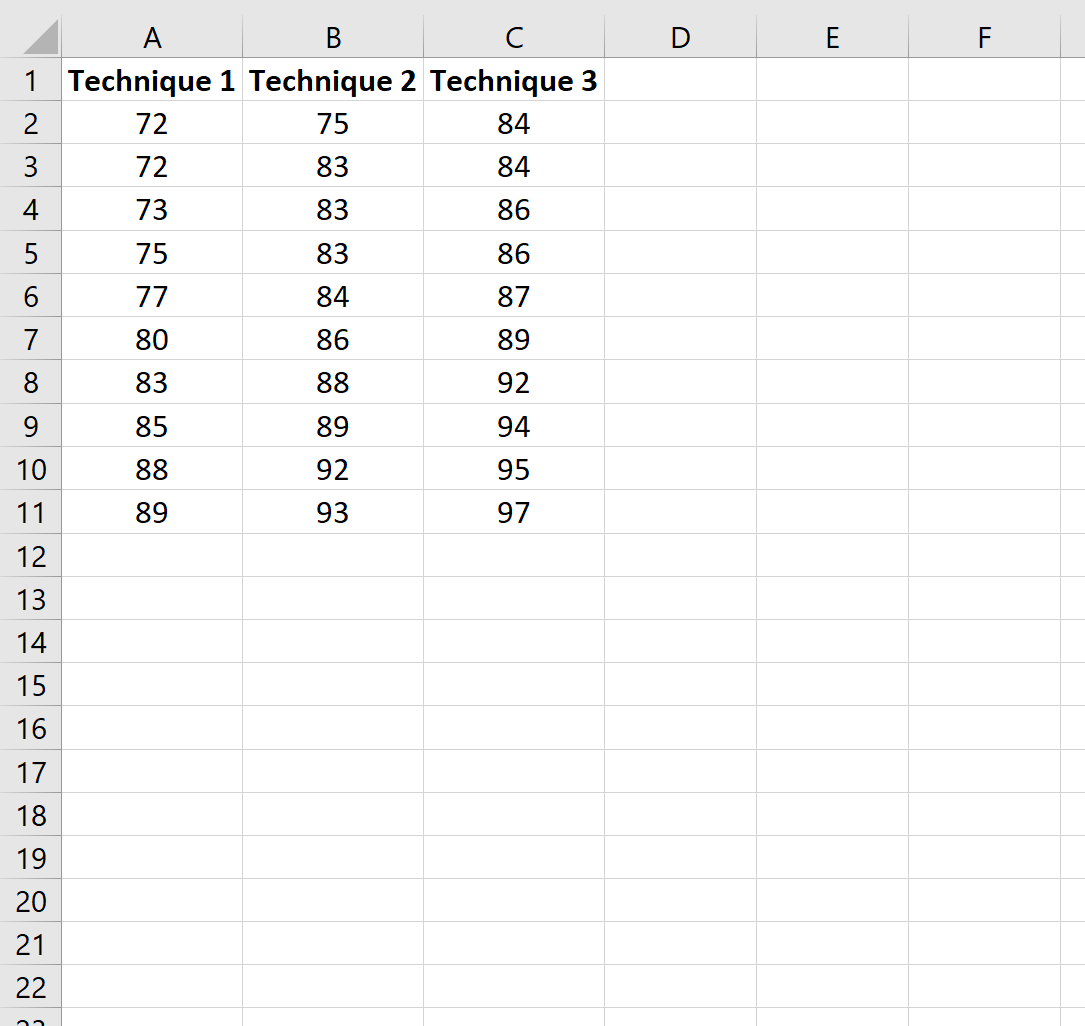
Крок 2: Виконайте односторонній дисперсійний аналіз
Далі виконаємо односторонній дисперсійний аналіз, щоб визначити, чи рівні середні бали за іспит у трьох групах.
Спочатку виділіть усі дані, включаючи заголовки стовпців:
Потім клацніть вкладку «Дані» на верхній стрічці, а потім клацніть «Аналіз даних» :

Якщо цей параметр недоступний, ви повинні спочатку завантажити Analysis ToolPak .
У вікні, що з’явиться, клацніть Anova: Single Factor , а потім натисніть OK .
Заповніть таку інформацію, а потім натисніть OK :
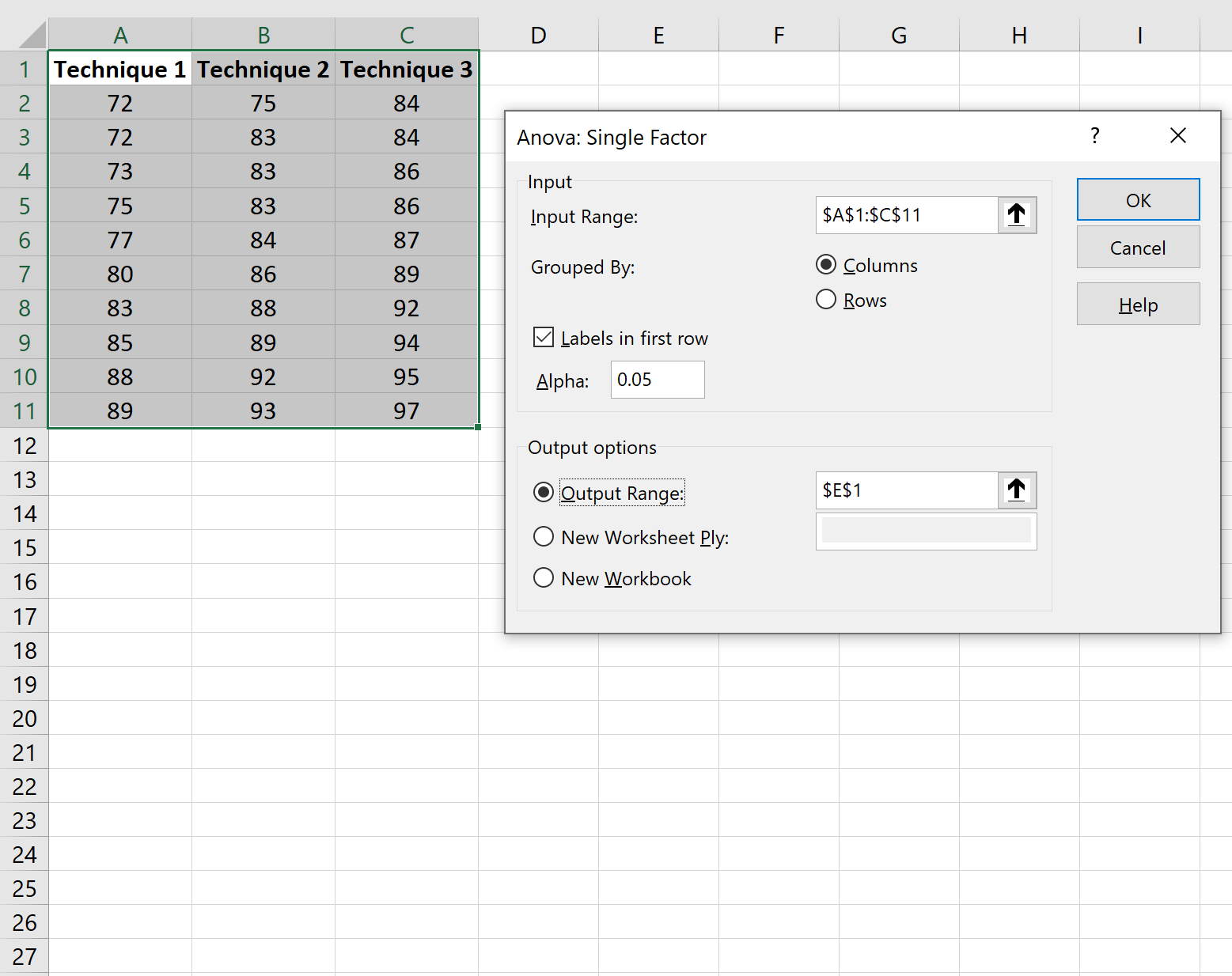
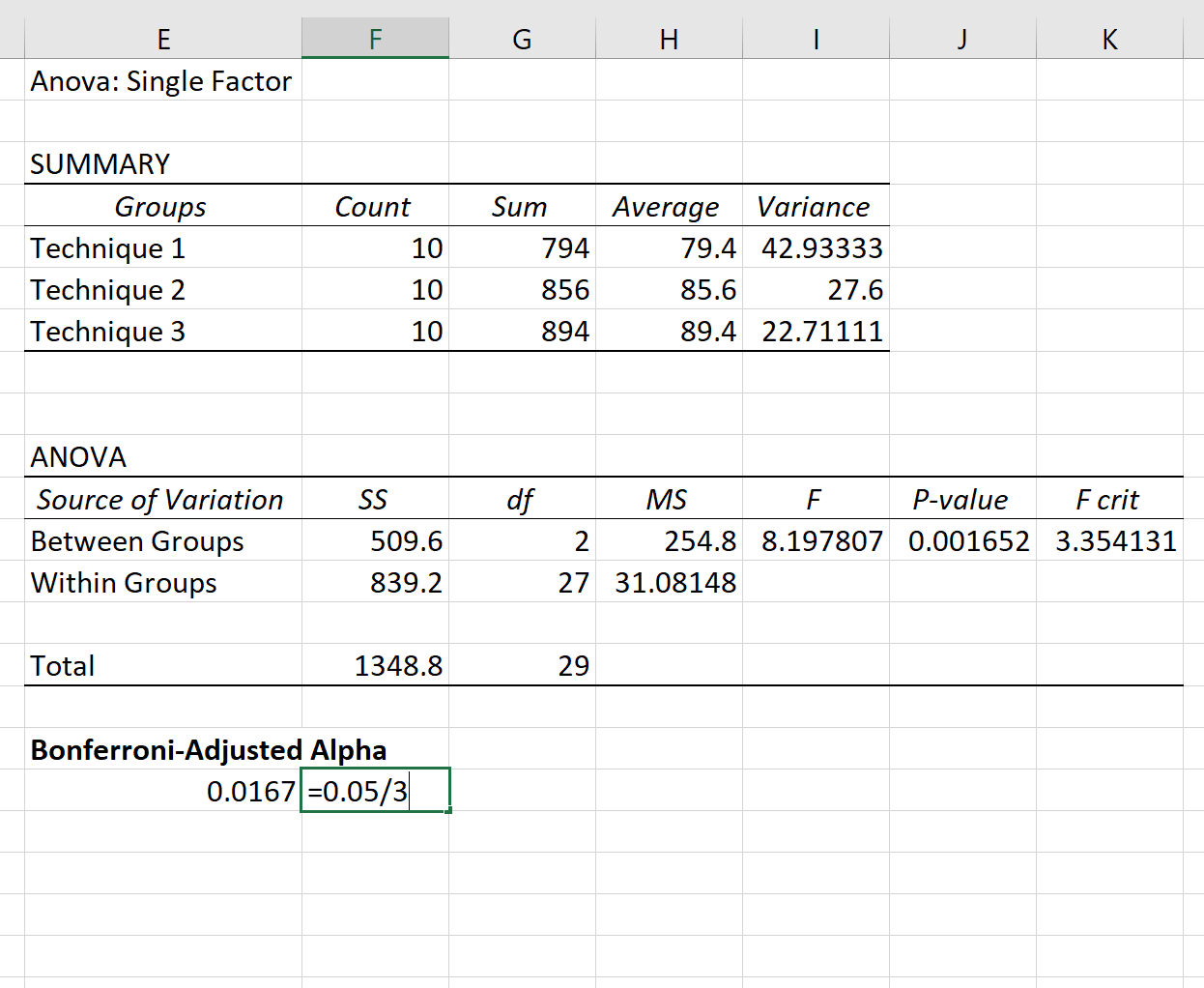
Результати одностороннього дисперсійного аналізу з’являться автоматично:
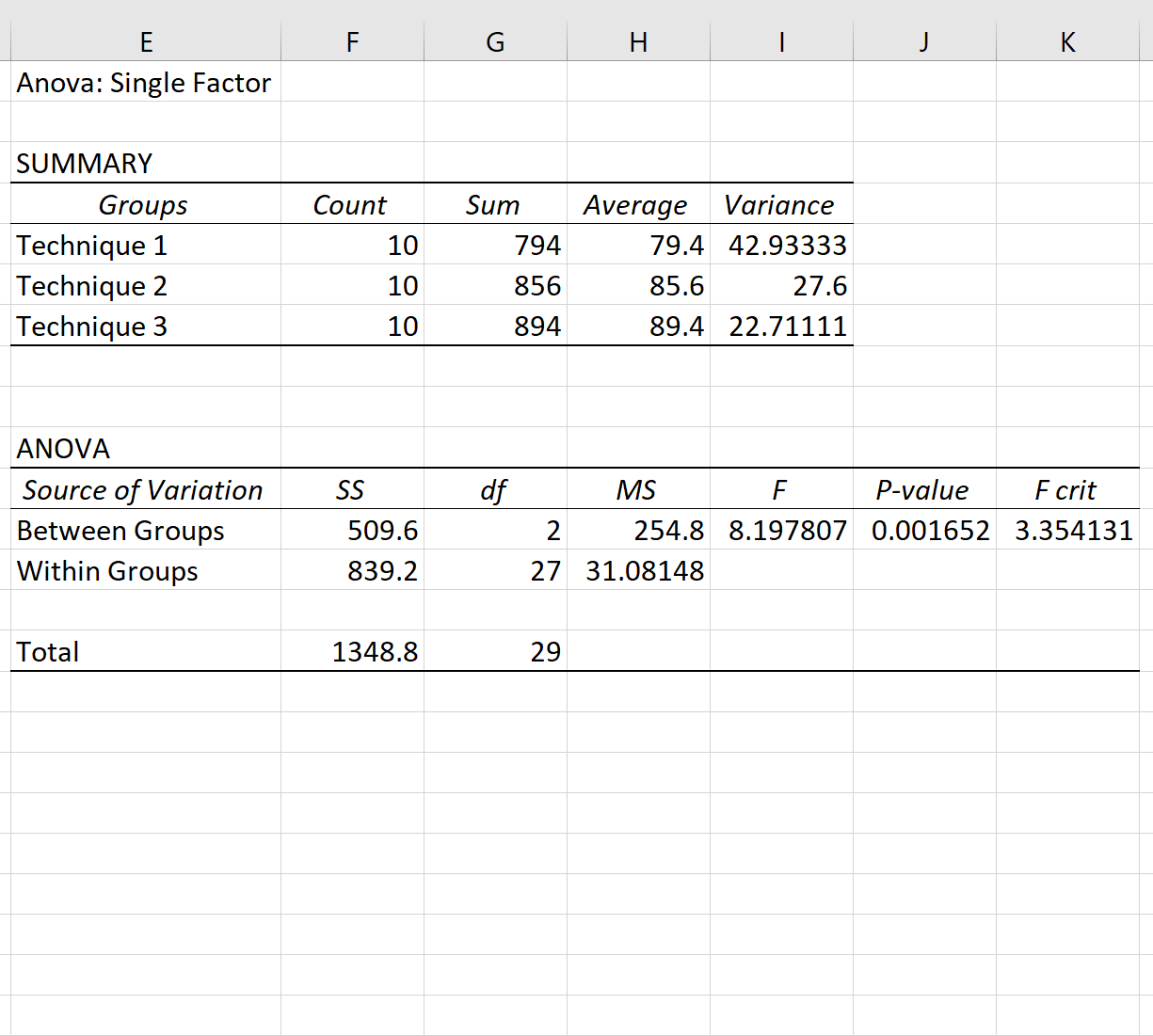
Нагадаємо, що односторонній дисперсійний аналіз має такі нульові та альтернативні гіпотези:
- H 0 (нульова гіпотеза): усі групові середні рівні.
- H A (альтернативна гіпотеза): принаймні одне групове середнє значення відрізняється відпочинок.
Оскільки p-значення в таблиці ANOVA (0,001652) менше 0,05, ми маємо достатньо доказів, щоб відхилити нульову гіпотезу. Іншими словами, середні бали за іспит у трьох груп не однакові.
Тоді ми можемо зробити кілька порівнянь за допомогою поправки Бонферроні між трьома групами, щоб точно побачити, які групові середні відрізняються.
Крок 3: Виконайте кілька порівнянь за допомогою поправки Бонферроні
Використовуючи поправку Бонферроні, ми можемо розрахувати скоригований рівень альфа наступним чином:
α новий = α оригінальний / n
У нашому прикладі ми виконаємо наступні три порівняння:
- Техніка 1 проти Техніки 2
- Техніка 1 проти Техніки 3
- Техніка 2 проти Техніки 3
Оскільки ми хочемо використовувати α = 0,05 для кожного тесту, поправка Бонферроні говорить нам, що ми повинні використовувати α new = 0,0167 .
Далі ми використаємо t-критерій для порівняння середніх між кожною групою. В Excel можна використовувати такий синтаксис:
=TTEST(Таблиця1, Таблиця2, черги=2, тип=2)
золото:
- Array1: перший масив даних
- Array2: другий масив даних
- tails: кількість хвостів у тесті. Ми будемо використовувати «2» для позначення двостороннього тесту.
- тип: тип t-критерію для виконання. Ми будемо використовувати «2», щоб позначити t-критерій з однаковими дисперсіями.
На наступному знімку екрана показано, як виконувати кожен t-тест:
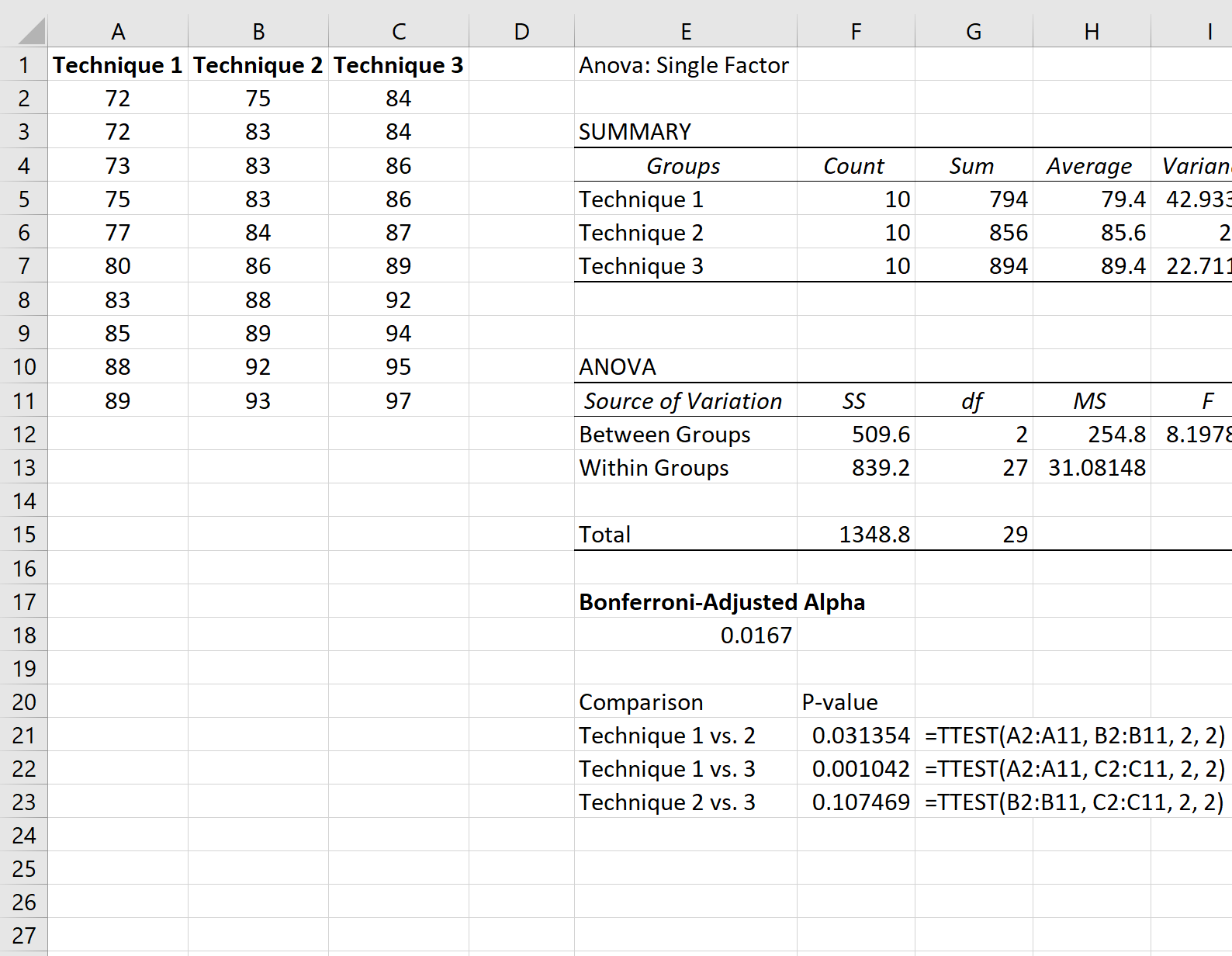
Єдине значення p нижче альфа-рівня, скоригованого за Бонферроні, отримано в результаті порівняння між технікою 1 і технікою 2, які мали значення p 0,001042 .
Таким чином, ми могли б зробити висновок, що лише статистично значуща різниця в середніх результатах іспиту була між технікою 1 і технікою 2.
Додаткові ресурси
Який рівень помилок на сім’ю?
Поправка Бонферроні: визначення та приклад
Калькулятор поправок Бонферроні