Кореляційна матриця

за Редакція 5 Серпня, 2023 Статистика 0 коментарів

У цій статті ви дізнаєтесь, що таке кореляційна матриця, яка її формула та як інтерпретувати кореляційну матрицю. Крім того, ви зможете побачити конкретний приклад інтерпретації кореляційної матриці.

Що таке кореляційна матриця?

Кореляційна матриця – це матриця, яка містить у позиції i,j коефіцієнт кореляції між змінними i та j .

Таким чином, кореляційна матриця – це квадратна матриця, заповнена одиницями на головній діагоналі, а елемент рядка i і стовпця j складається зі значення коефіцієнта кореляції між змінною i і змінною j .

Таким чином , формула для кореляційної матриці виглядає наступним чином:

золото

$r_{ij}$

– коефіцієнт кореляції між змінними

$i$

$j.$

Отже, щоб знайти кореляційну матрицю набору даних, важливо знати, як обчислюється коефіцієнт кореляції. Якщо ви не пам’ятаєте, за наступним посиланням ви дізнаєтеся, як це зробити за допомогою онлайн-калькулятора:

➤ Дивіться: калькулятор коефіцієнта кореляції

Властивістю коефіцієнта кореляції є те, що порядок змінних не має значення для його розрахунку, тобто коефіцієнт кореляції

$r_{ij}$

еквівалентно

$r_{ji}.$

Отже, кореляційна матриця є симетричною.

$\displaystyle R=\begin{pmatrix}1&r_{12}&r_{13}&\dots&r_{1n}\\[1.1ex] r_{12}&1&r_{23}&\dots&r_{2n}\\[1.1ex] r_{13}&r_{23}&1&\dots&r_{3n}\\[1.1ex] \vdots &\vdots &\vdots &\ddots &\vdots\\[1.1ex] r_{1n}&r_{2n}&r_{3n}&\dots&1\end{pmatrix}$

Щоб кореляційна матриця була значущою, набір статистичних даних повинен містити більше двох змінних. В іншому випадку достатньо було б визначити єдиний коефіцієнт кореляції, і кореляційна матриця мала б сенс.

Як скласти кореляційну матрицю

З огляду на визначення кореляційної матриці, давайте подивимося, як створюється цей тип статистичної матриці:

Обчисліть коефіцієнт кореляції кожної пари змінних. Зверніть увагу, що порядок змінних не змінює результат, тому його потрібно обчислити лише один раз для кожної пари змінних.
Створіть квадратну матрицю того самого розміру, що й кількість змінних у ряді даних. Ця матриця буде кореляційною матрицею.
Поставте 1 у кожному елементі головної діагоналі кореляційної матриці.
Поставте коефіцієнт кореляції змінних i , j на позиції i , j та j , i .
Після створення кореляційної матриці залишається лише інтерпретувати її значення.

Майте на увазі, що просто запустити кореляційну матрицю недостатньо, потім потрібно інтерпретувати її значення та розуміти, що вони означають. У наступному розділі пояснюється, як інтерпретувати кореляційну матрицю.

Інтерпретація кореляційної матриці

Для правильної інтерпретації кореляційної матриці необхідно врахувати, що значення коефіцієнта кореляції може коливатися від -1 до +1:

r=-1 : дві змінні мають ідеальну негативну кореляцію, тому ми можемо намалювати лінію з негативним нахилом, у якій усі точки пов’язані.
-1<r<0 : кореляція між двома змінними негативна, тому коли одна змінна зростає, інша зменшується. Чим ближче значення до -1, тим більше негативно пов’язані змінні.
r=0 : кореляція між двома змінними дуже слабка, фактично лінійна залежність між ними дорівнює нулю. Це не означає, що змінні є незалежними, оскільки вони можуть мати нелінійний зв’язок.
0<r<1 : кореляція між двома змінними позитивна, чим ближче значення до +1, тим сильніший зв’язок між змінними. У цьому випадку одна змінна має тенденцію до збільшення свого значення, коли інша також збільшується.
r=1 : дві змінні мають ідеальну позитивну кореляцію, тобто вони мають позитивну лінійну залежність.

Таким чином, щоб інтерпретувати кореляційну матрицю, необхідно інтерпретувати кожен коефіцієнт кореляції та порівнювати різні результати.

Таким чином ви зможете побачити, які змінні найбільш пов’язані одна з одною, які змінні є найважливішими, які змінні практично не пов’язані одна з одною тощо.

Приклад кореляційної матриці

Щоб повністю зрозуміти, з чого складається кореляційна матриця та як вона інтерпретується, у цьому розділі ми розберемо приклад кореляційної матриці:

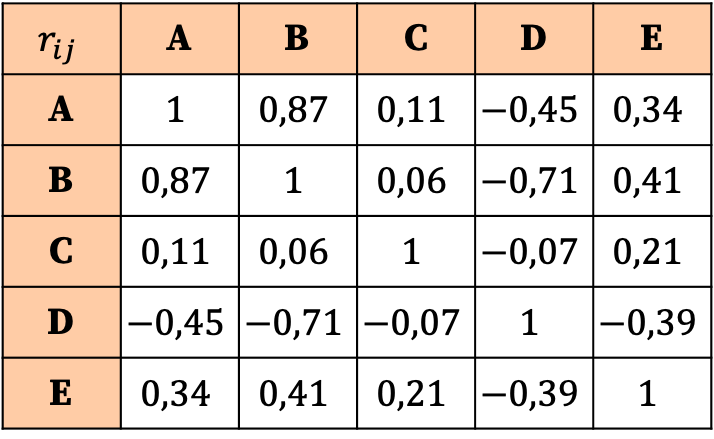
Інтерпретація кореляційної матриці заснована на значеннях коефіцієнтів. Таким чином, ми бачимо, що найсильнішою кореляцією є зв’язок між змінною А та змінною В, оскільки її відповідний коефіцієнт є найбільшим (0,87).

З іншого боку, змінна C практично не корелює з жодною змінною, оскільки всі її коефіцієнти дуже близькі до нуля і тому дуже низькі. Таким чином, щоб спростити аналіз, ми могли б навіть розглянути можливість видалення цієї змінної зі статистичного дослідження.

Подібним чином усі зв’язки змінної D з іншими змінними є негативними, тобто кореляція між змінною D та іншими змінними є зворотною. Це не означає, що змінна повинна бути виключена, просто те, що змінна D негативно корельована.

Як бачите, кореляційна матриця дуже корисна для узагальнення даних і проведення загального аналізу зв’язку між різними змінними в наборі даних.

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше