Як створити кореляційну матрицю в spss

Кореляційна матриця – це квадратна таблиця, яка показує коефіцієнти кореляції Пірсона між різними змінними в наборі даних.

Нагадуємо, що коефіцієнт кореляції Пірсона є мірою лінійного зв’язку між двома змінними . Він приймає значення від -1 до 1, де:

• -1 вказує на абсолютно негативну лінійну кореляцію між двома змінними
• 0 означає відсутність лінійної кореляції між двома змінними
• 1 вказує на абсолютно позитивну лінійну кореляцію між двома змінними

Чим далі коефіцієнт кореляції від нуля, тим сильніший зв’язок між двома змінними.

Цей посібник пояснює, як створити та інтерпретувати кореляційну матрицю в SPSS.

Приклад: як створити кореляційну матрицю в SPSS

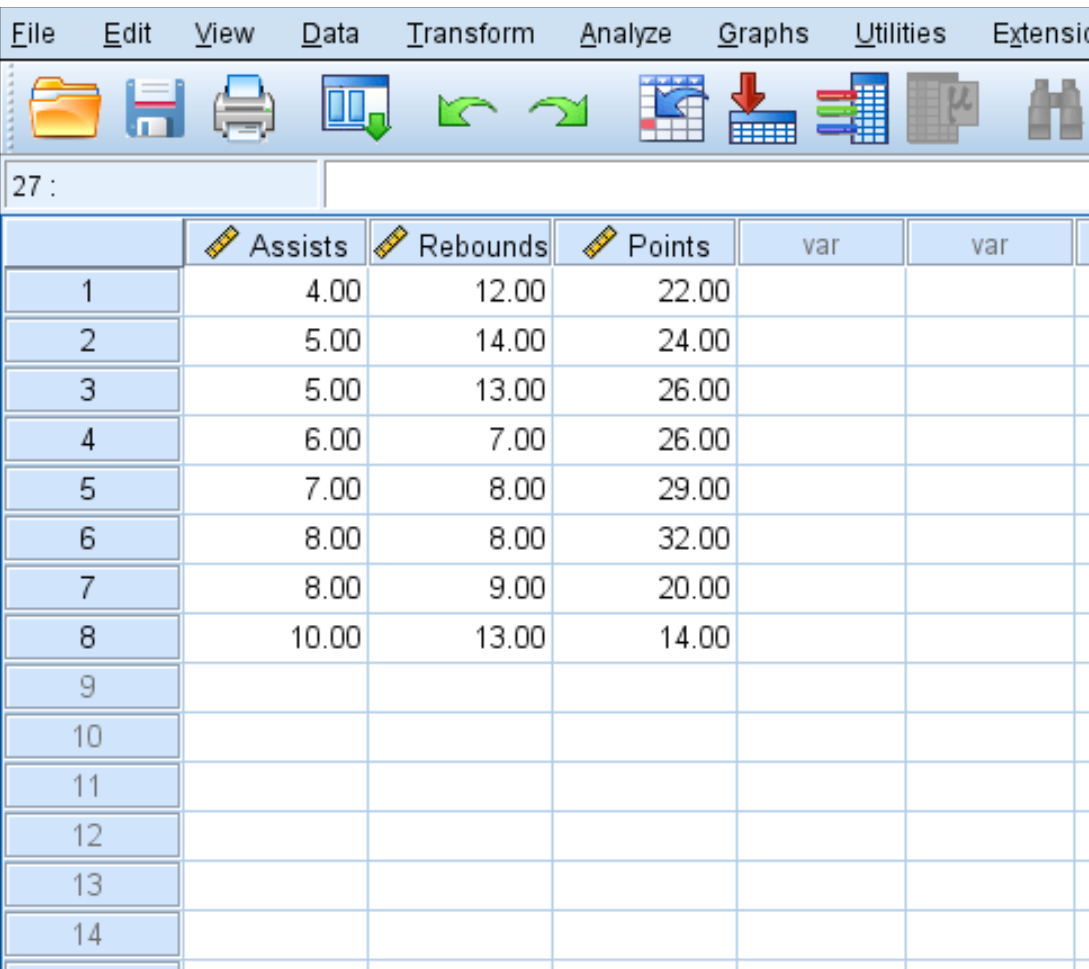
Виконайте наступні дії, щоб створити кореляційну матрицю для цього набору даних, яка відображає середню кількість передач, підбирань і очок восьми баскетболістів:

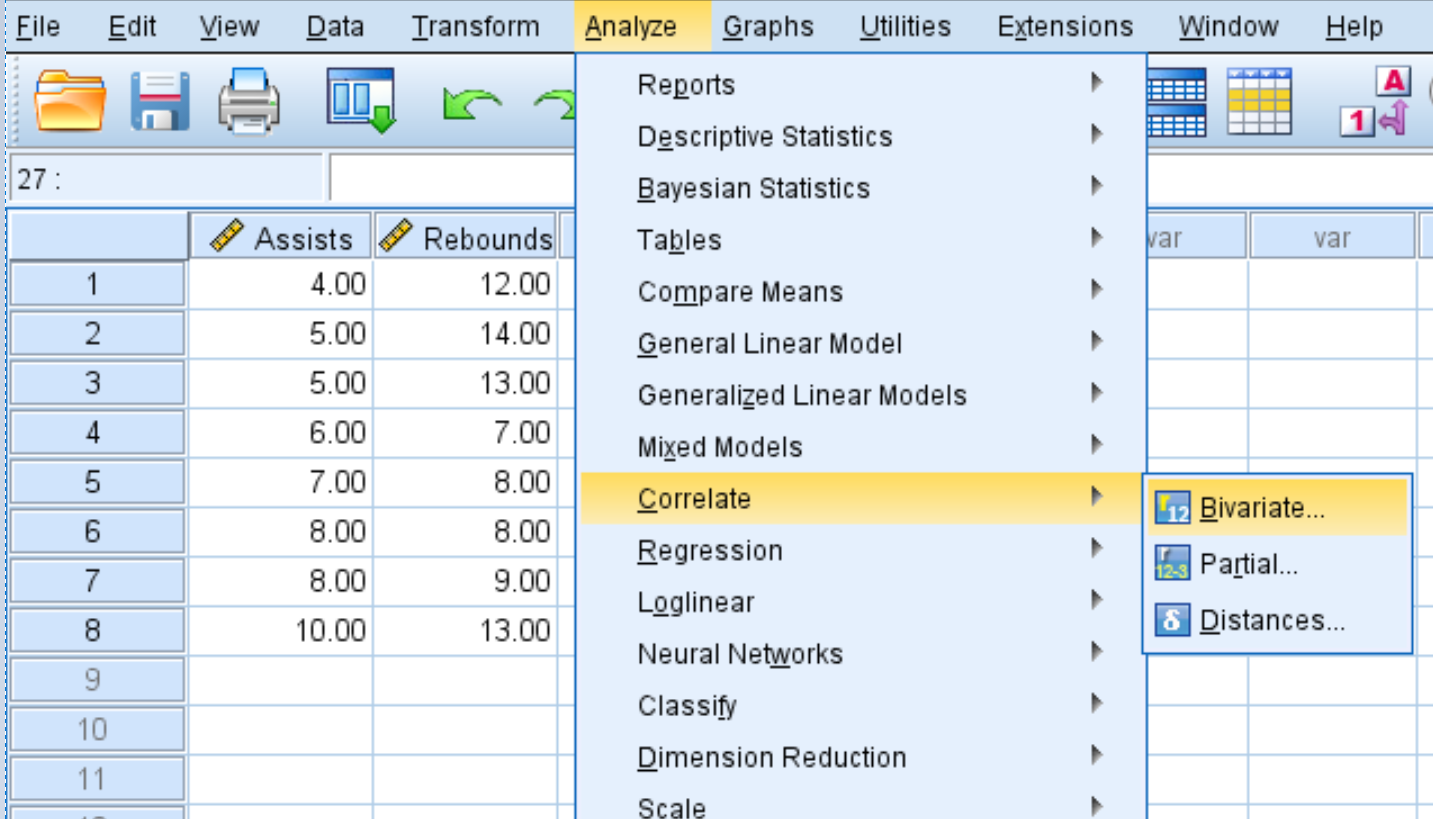
Крок 1: Виберіть двовимірну кореляцію.

• Перейдіть на вкладку Аналіз .
• Натисніть «Споставити» .
• Натисніть Двоваріантний .

Крок 2: Створіть кореляційну матрицю.

Кожна змінна в наборі даних спочатку відображатиметься в лівому полі:

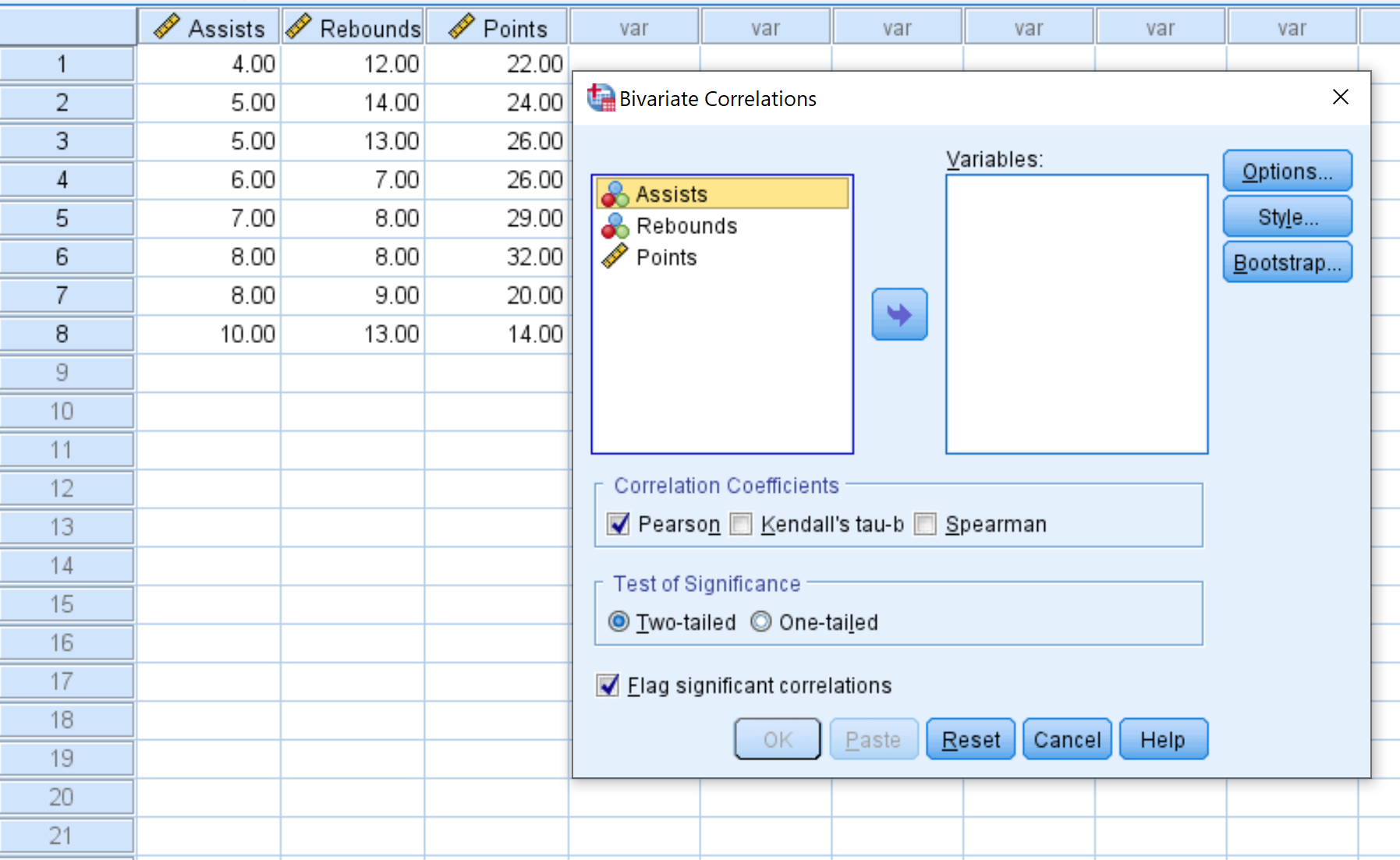
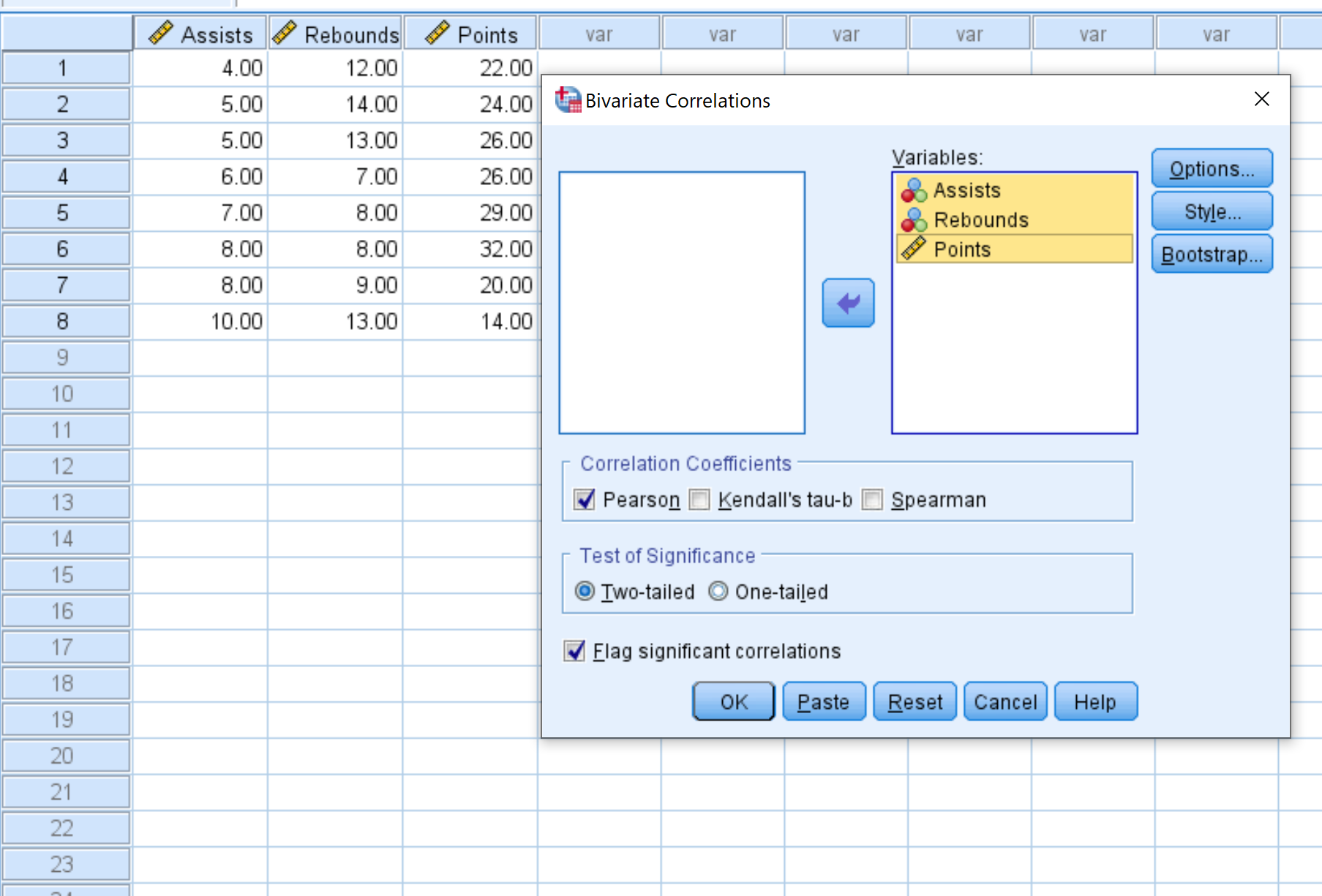
• Виберіть кожну змінну, яку потрібно включити до кореляційної матриці, і клацніть стрілку, щоб перенести їх у вікно Змінні . У цьому прикладі ми будемо використовувати всі три змінні.
• У розділі «Коефіцієнти кореляції» виберіть, чи потрібно використовувати кореляцію Пірсона, тау Кендалла чи кореляцію Спірмена. Ми залишимо це як Pearson для цього прикладу.
• У розділі «Тест значущості» виберіть, чи бажаєте ви використовувати двобічний чи однобічний тест, щоб визначити, чи мають дві змінні статистично значущий зв’язок. Ми залишимо це двостороннім.
• Поставте прапорець поруч із пунктом «Повідомити про значні кореляції» , якщо ви хочете, щоб SPSS повідомляв про змінні, які мають значну кореляцію.
• Нарешті натисніть OK .

Після натискання кнопки OK з’явиться така кореляційна матриця:

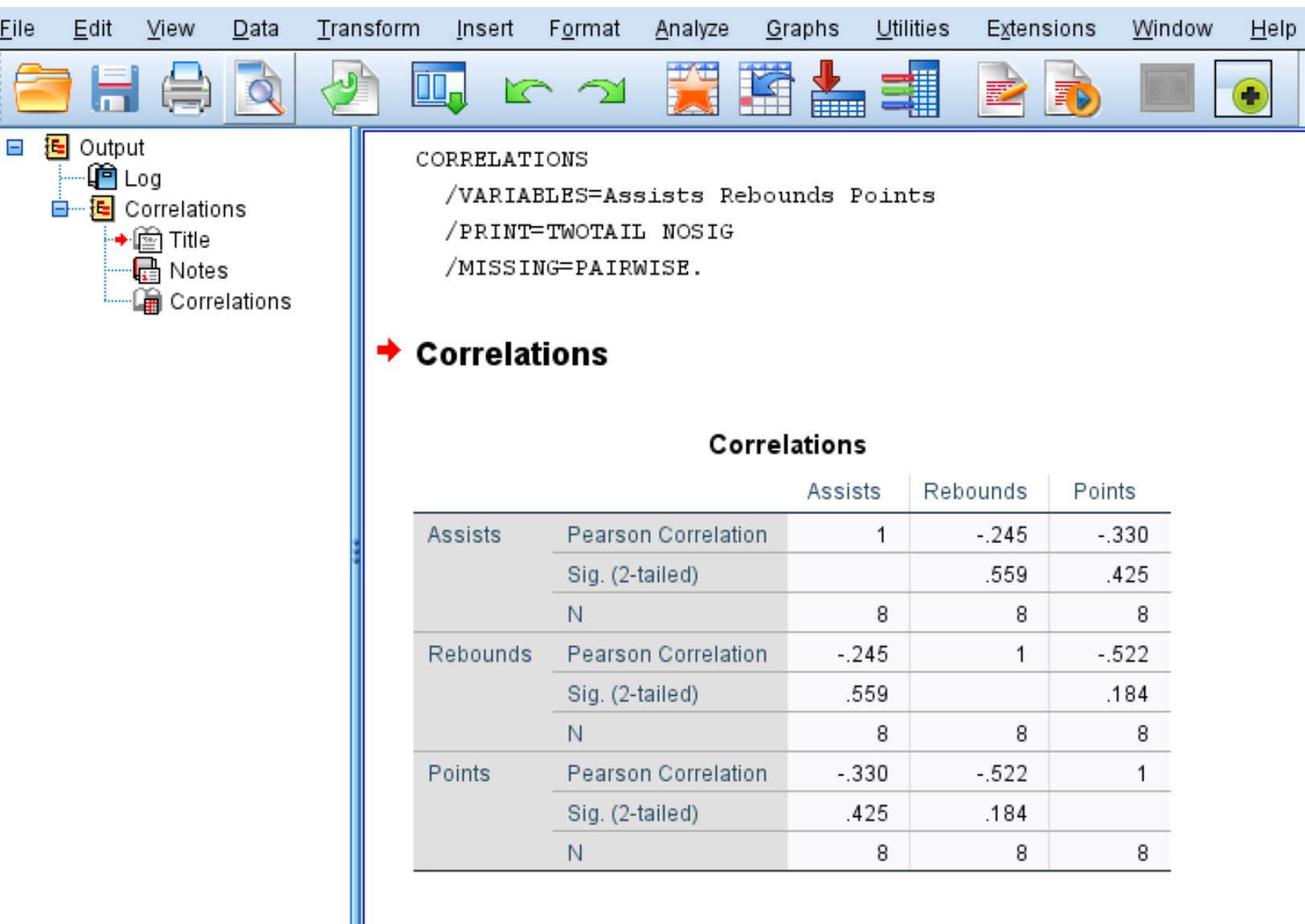
Крок 3: Інтерпретація кореляційної матриці.

Кореляційна матриця відображає наступні три вимірювання для кожної змінної:

• Кореляція Пірсона: міра лінійного зв’язку між двома змінними в діапазоні від -1 до 1.
• Sig. (двостороннє): двостороннє значення p, пов’язане з коефіцієнтом кореляції. Це означає, що дві змінні мають статистично значущий зв’язок (наприклад, якщо p < 0,05)
• N: кількість пар, використаних для розрахунку коефіцієнта кореляції Пірсона.

Наприклад, ось як інтерпретувати результат змінної Assists:

• Коефіцієнт кореляції Пірсона між передачами та підбираннями становить -0,245 . Оскільки це число негативне, це означає, що ці дві змінні мають негативний зв’язок.
• P-значення, пов’язане з коефіцієнтом кореляції Пірсона для передач і підбирань, становить 0,559 . Оскільки це значення не менше 0,05, дві змінні не мають статистично значущого зв’язку.
• Кількість пар, використаних для розрахунку коефіцієнта кореляції Пірсона, становила 8 (наприклад, у цьому розрахунку було використано 8 пар гравців).

Крок 4: Візуалізуйте кореляційну матрицю.

Ви також можете створити матрицю діаграми розсіювання, щоб візуалізувати лінійний зв’язок між кожною зі змінних.

• Перейдіть на вкладку Діаграми .
• Натисніть Конструктор діаграм .

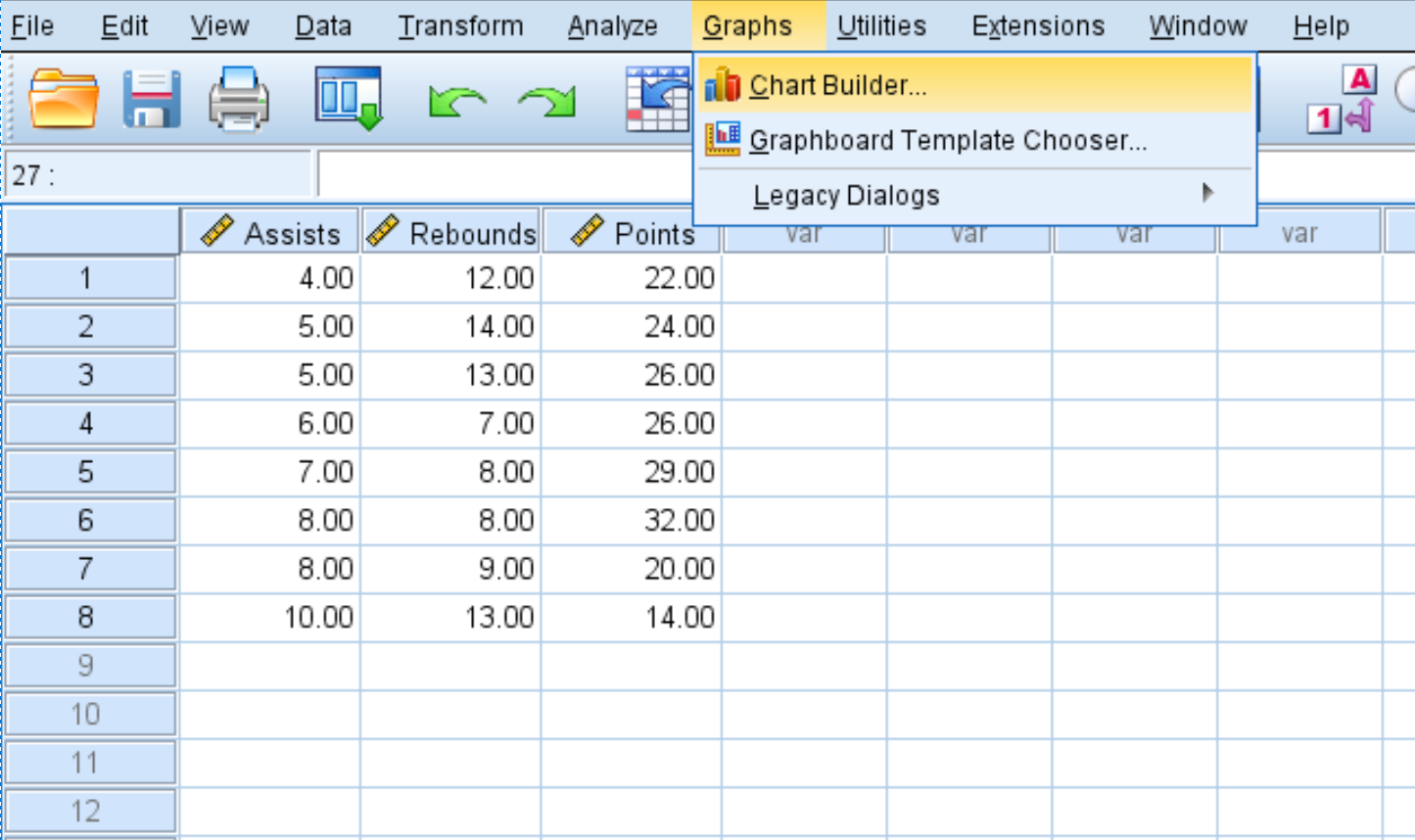
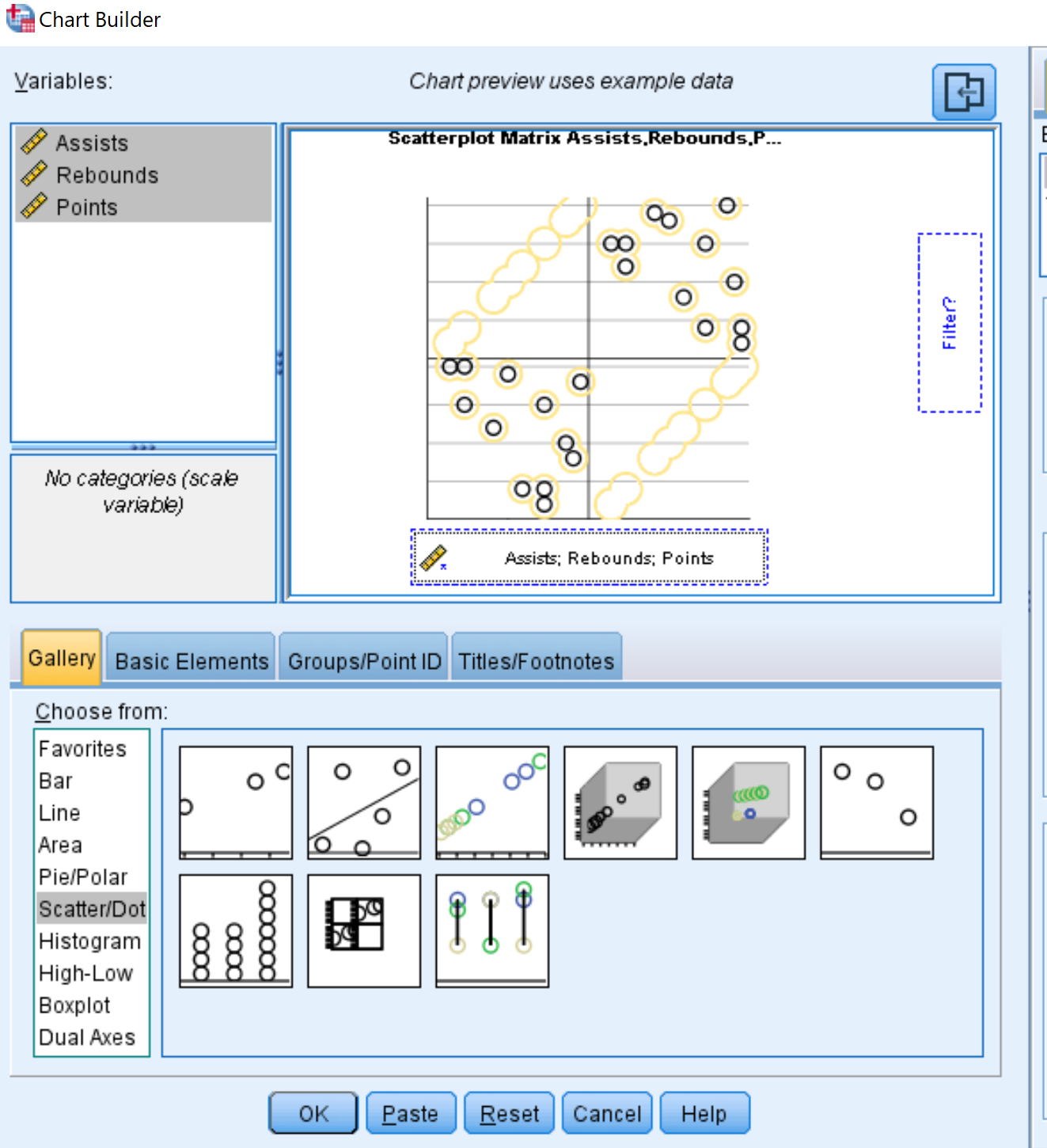
• Для типу діаграми клацніть Точкова/точкова діаграма .
• Натисніть на зображення з написом Scatterplot Matrix .
• У полі «Змінні» вгорі ліворуч утримуйте клавішу Ctrl і клацніть назви трьох змінних. Перетягніть їх у поле внизу діаграми з написом Scattermatrix .
• Нарешті натисніть OK .

Автоматично з’явиться наступна матриця діаграми розсіювання:

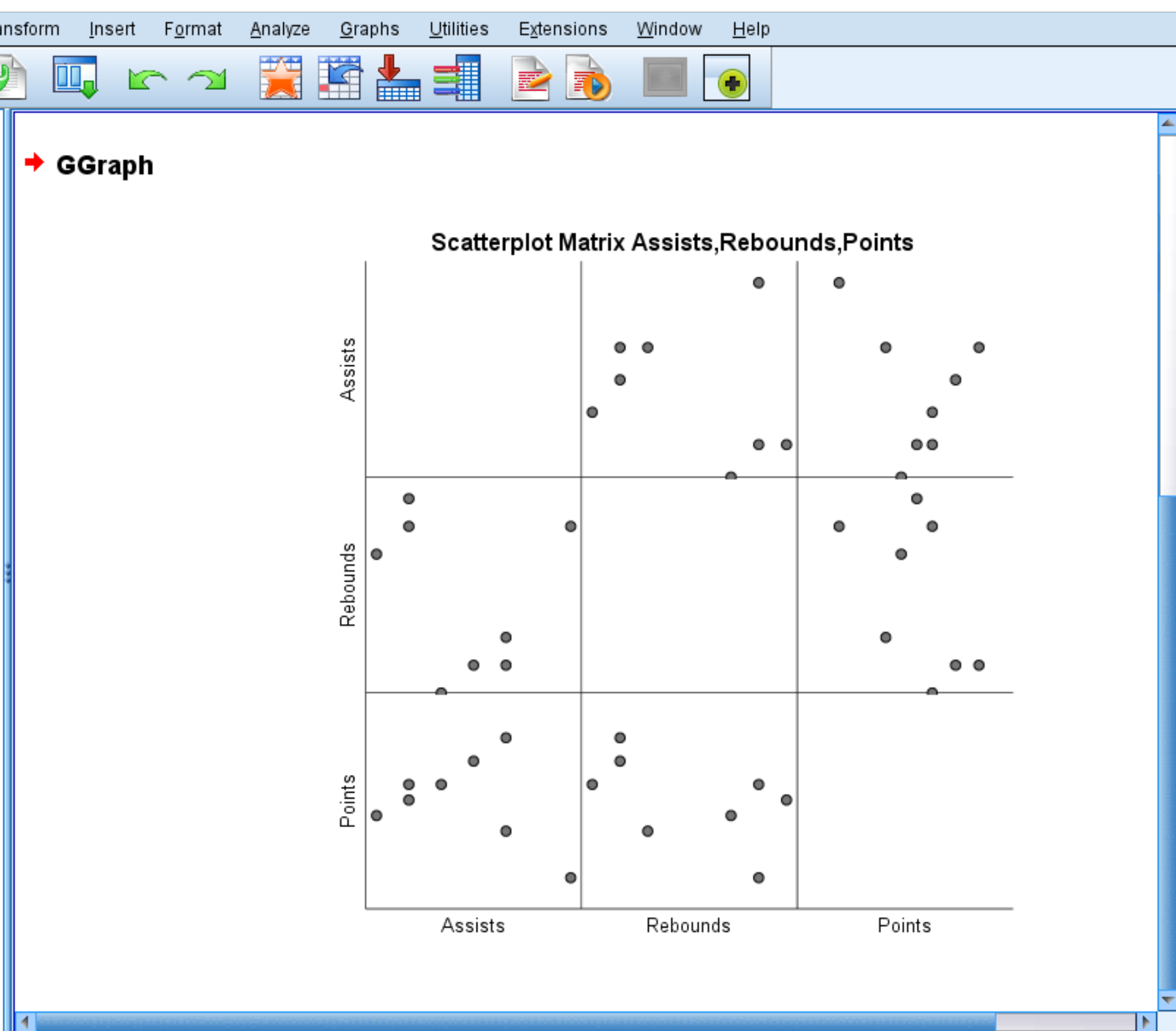
Кожна окрема діаграма розсіювання показує попарні комбінації між двома змінними. Наприклад, діаграма розсіювання в нижньому лівому куті показує попарні комбінації очок і передач для кожного з 8 гравців у наборі даних.

Матриця діаграми розсіювання є необов’язковою, але вона забезпечує хороший спосіб візуалізації зв’язку між кожною попарною комбінацією змінних у наборі даних.