Ділянка коробки та вуса

за Редакція 5 Серпня, 2023 Статистика 0 коментарів

У цій статті пояснюється, що таке boxplot, також відомий як boxplot (або boxplot). Ви дізнаєтесь, як створюються ці типи статистичних діаграм, а також розв’яжете вправу на діаграмі коробки та вусів та її інтерпретацію.

Що таке графік коробки та вуса?

Боксплот , також званий боксплотом або боксплотом , — це графік, який візуально представляє набір статистичних даних за допомогою квартилів.

Основною характеристикою прямокутної діаграми є те, що вона дозволяє швидко візуалізувати дисперсію ряду даних, оскільки вона вказує на квартилі, медіану, екстремальні значення та викиди даних.

Таким чином, цей тип діаграми складається з прямокутної рамки та кількох ліній (або вусів), з яких виходять такі значення:

Межі прямокутника вказують на перший і третій квартилі (Q ₁ і Q ₃ ). А вертикальна лінія всередині прямокутника є медіаною (еквівалентна другому квартилю _Q2 ).
Межі вусів (або рук) є крайніми значеннями , тобто мінімальним значенням і максимальним значенням ряду даних.
Точки поза вусами є викидами , або, іншими словами, даними, які, ймовірно, були виміряні неправильно , і тому їх не слід брати до уваги в статистичному дослідженні.

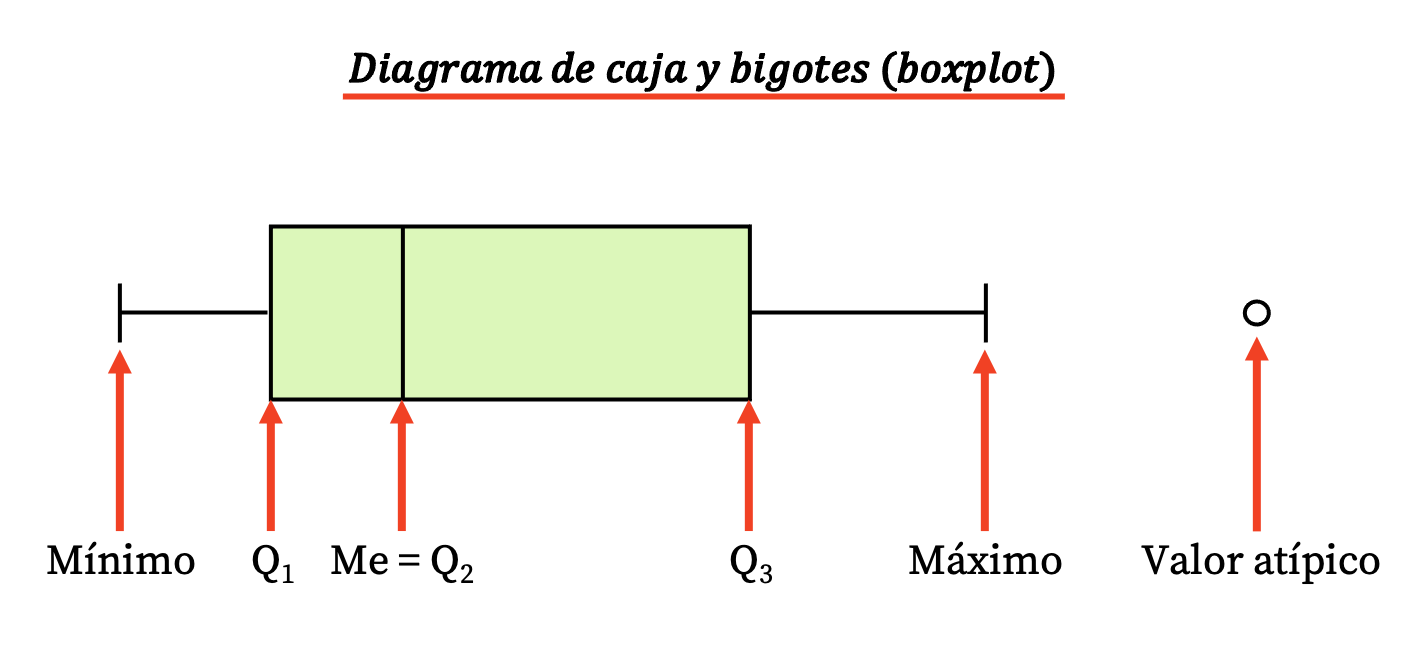
Зауважте, що різниця між третім і першим квартилем є інтерквартильним діапазоном (або інтерквартильним діапазоном), іншим показником статистичної дисперсії.

Коробчаті та вусисті графіки дуже корисні для порівняння числових змінних. Однак він не підходить для представлення категоріальних змінних.

Як створити діаграму коробки та вуса

Щоб створити прямокутну діаграму (або прямокутну діаграму) із ряду даних, необхідно виконати наступні кроки:

Розберіть приклади статистичних даних.
Обчисліть квартилі (Q ₁ , Q ₂ і Q ₃ ) і зобразіть їх у вигляді рамки на діаграмі. Перший і третій квартилі відповідають межам прямокутника, і щоб представити медіану (другий квартиль), ви повинні намалювати лінію всередині прямокутника, де розташоване його значення.
Обчисліть інтерквартильний діапазон, який дорівнює третьому квартилю мінус перший квартиль.

$IQR=Q_3-Q_1$

Обчислити допустимі величини LI і LS, формули яких:

$LI=Q_1-1,5\cdot IQR$

$LS=Q_3+1,5\cdot IQR$

Визначте вибіркові викиди, які є значеннями, меншими за LI або більшими за LS. Позначте ці значення за межами діапазону вусів крапками.
Визначте та відобразіть крайні значення, які є найменшим значенням і найбільшим значенням в інтервалі, утвореному LI та LS. Ці значення представляють кінець двох вусів на діаграмі.

Приклад графіка коробки та вуса

Розглянувши визначення та теорію прямокутної діаграми (або прямокутної діаграми), нижче ви знайдете конкретний приклад, щоб краще зрозуміти концепцію та побачити, як виконується цей тип статистичної діаграми.

Намалюйте коробковий графік наступного набору статистичних даних.

У цьому випадку дані вже впорядковано від найменшого до найбільшого, тому жодних змін не потрібно. В іншому випадку ми повинні спочатку відсортувати вибіркові дані.

По-друге, ми витягуємо квартилі вибірки:

$Q_1=4,06$

$Q_2=4,38$

$Q_3=4,66$

➤ Дивіться: квартильний калькулятор

Після того, як ми обчислили три квартилі, ми знаходимо інтерквартильний діапазон, віднімаючи квартиль 3 мінус квартиль 1:

$IQR=Q_3-Q_1=4,66-4,06=0,6$

Тепер ми обчислюємо межі LI і LS, які є значеннями, починаючи з яких дані вважаються нетиповими. Для цього необхідно використовувати такі формули:

$LI=Q_1-1,5\cdot IQR=4,06-1,5\cdot 0,6=3,16$

$LS=Q_3+1,5\cdot IQR=4,66+1,5\cdot 0,6=5,56$

Тож у цьому випадку ми маємо два викиди, оскільки 3,02 менше за 3,16, а 5,71 більше за 5,56.

$\text{Valores at\'ipicos} =\Bigl\{3,02 \ ; \ 5,71\Bigr\}$

Нарешті, залишається визначити крайні значення, які є мінімумом і максимумом усіх даних, які знаходяться в інтервалі [LI,LS]. Тому в нашому прикладі мінімальне значення становить 3,70, а максимальне значення – 4,81.

$\text{M\'inimo}=3,70$

$\text{M\'aximo}=4,81$

Отже, коли ми визначили всі значення коробки та діаграми вусів, все, що залишилося, це зробити графічне представлення:

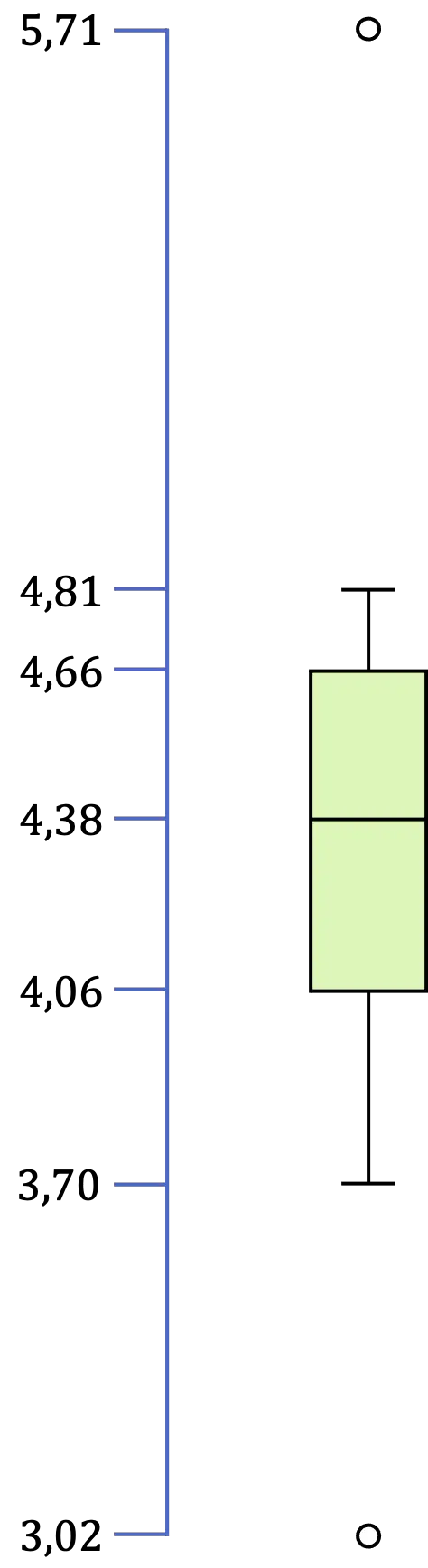
Для чого використовується графік коробки та вуса?

Нарешті, давайте подивимося, для чого це потрібно і як інтерпретувати діаграму коробки та вусів (або коробчату діаграму).

Очевидно, що прямокутний графік дуже корисний для швидкого визначення квартилів, інтерквартильного діапазону, медіани, екстремальних значень і викидів ряду даних, оскільки всі ці статистичні показники можна ідентифікувати простим переглядом.

Крім того, прямокутний графік використовується для аналізу симетрії статистичної вибірки, оскільки він візуально представляє весь набір даних. Якщо медіана знаходиться не в центрі прямокутника, це означає, що вибірка не симетрична.

Подібним чином коробкові діаграми широко використовуються на фондовому ринку для представлення зміни ціни акції протягом певного періоду часу, оскільки вони дозволяють побачити максимальне значення, мінімальне значення та проміжні значення за короткий період часу. час і таким чином швидше приймати рішення.

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше